Равномерное прямолинейное движение: задачи с решениями

• задачи с решениями

• кинематика

• механика

• прямолинейное движение

• равномерное движение

1) Выяснить скорость двух тел, написать уравнения скорости и пути по представленным графикам зависимости скорости от времени и координаты тела от времени. [условие полностью] [решение]

Задача 1: график зависимости координаты от времени

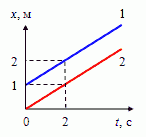На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути, пройденного телом, от времени? Решение

На рисунке показаны графики равномерного движения тел. 1) В начальный момент времени t = 0 первое тело имеет начальную координату х_о1 = 1 м, второе тело — координату х_о2 = 0. 2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени. 3) Уравнение движения для равномерного прямолинейного движения имеет вид: x=x_о+v_хt. Тогда для первого, второго тела соответственно: x₁=x_о1+v_1хt и x₂=x_о2+v_2хt или x₁=1+v_1хt, x₂=v_2хt. Определим скорости первого и второго тела:

v1x	=	x1 − 1	=	2 − 1	= 0,5 м/с.
		t		2

v2x	=	x2	=	1	= 0,5 м/с.
		t		2

Уравнения скорости имеют вид: v_1х=v_2х=0,5 м/с. Так как S=v_хt, то уравнение пути S=0,5t.

2) Определить скорости, пути, момент встречи тел по графику движений двух тел. [условие полностью] [решение]

Задача 2: встреча тел на графике движения

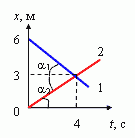Графики каких движений показаны на рисунке? Как отличаются скорости движения этих тел? В какой момент времени тела встретились? Какие пути тела прошли до встречи? Смотрите решение. Решение

Так как изменение координаты тела происходит прямо пропорционально времени, то можно утверждать, что движение равномерное и прямолинейное. По отношению к точке отсчета (0; 0) у первого тела координата убывает, а у второго наоборот — возрастает. Первое тело движется против оси х, второе — по направлению оси координат. а) Чтобы ответить на вопрос об отличии скоростей, определим их из уравнения координаты:

vx	=	x − xo	, тогда
		t

v1x	=	3 − 6	м/с = −0.75 м/с.
		4

v2x	=	3 − 0	м/с = 0.75 м/с.
		4

Скорости тел равны по абсолютному значению, но противоположны по направлению. б) Зная также, что v=tg α (геометрический смысл скорости) и сравнивая углы наклонов графиков движения тел к оси t, приходим к выводу, что углы одинаковы, следовательно, скорости равны. в) Точка пересечения двух прямых означает, что тела встретились в одно и то же время в одной и той же точке, т. е. время встречи t = 4 c, а координата x = 3 м. г) Так как движение равномерное и прямолинейное, то S = x − x_o. Находим пути, пройденные телами до встречи: S₁= | x₁ − x_o1 | = | (3−6) м | = 3 м, S₂= | x₂ − x_o2 | = | (3−0) м | = 3 м. Оба тела, двигаясь с одинаковыми скоростями, за одно и тоже время прошли равное расстояние.

3) Написать уравнение движения точки и уравнение траектории по известной начальной скорости, углу наклона к оси X и координатам в начальный момент времени. [условие] [решение]

Точка движется с постоянной скоростью v_o под углом α к оси x. В начальный момент времени t = 0 точка имела координаты (х_o; у_o). Написать уравнения движения точки и уравнение траектории.

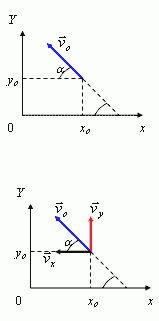Решение (исправлено 25.11.2010):

уравнение движения имеет вид: x = x_o + v_xt по оси x и y = y_o + v_yt по оси Y. Начальные координаты заданы x_o, y_o. Проекции скорости найдем из прямоугольного треугольника АВС: v_x = −v_ocos α, знак минус указывает на то, что направление проекции вектора скорости не совпадает с направлением оси x; v_y = v_osin α, проекция скорости положительна, так как направление вектора скорости, совпадает с направлением оси Y. Тогда, подставляя проекции скоростей в соответствующие уравнения движения, имеем: x = x_o − v_ot·cos α, y = y_o + v_ot·sin α. Решая совместно эти два уравнения, напишем уравнение траектории. Для этого из уравнения движения точки вдоль оси x выразим время и подставим в уравнение движения точки вдоль оси Y:

t =	xo − x	, тогда
	vo cos α

y = yo + vo sin α	xo − x	=	yo + xotg α − x tg α.
	vo cos α