С_усл = 1 – 2 + 1 = 0,

система безвариантна – в этой точке нельзя менять ни один параметр (температура, состав), не нарушив равновесия.

В точке I число независимых компонентов К = 2; (число фаз Ф = 2 (жидкость и пар),

С_усл = 2 – 2 + 1 = 1,

у системы есть одна степень свободы.

В точке О число независимых компонентов К = 2, число фаз Ф = 2 (жидкость и пар). Следует учесть, что в данном случае в уравнение (68) вводится дополнительное ограничение, связанное с тем, что состав жидкости и состав пара одинаков.

С_усл = 2 – 1 - 2 + 1 = 0,

в этой точке нельзя менять ни один параметр (температура, состав), не нарушив равновесия.

Задача №22

Два вещества (А и В) не образуют твердых растворов, но в расплавленном состоянии смешиваются друг с другом в любых соотношениях. Постройте диаграмму фазового состояния (диаграмму плавкости) двухкомпонентной системы (А - В), зная температуру начала кристаллизации системы (табл. 21, состав задан по веществу А, мольн.%).

1. Обозначьте точками: I – жидкий плав, содержащий а% вещества А при температуре T₁; II – плав, содержащий а% вещества А, находящийся в равновесии с кристаллами химического соединения; III – систему, состоящую из твердого вещества А в равновесии с расплавом, содержащим б% вещества А; IV – равновесие трех фаз (табл. 22).

2. Определите составы химических соединений.

3. Определите качественные и количественные составы эвтектик.

4. Определите число фаз и число термодинамических степеней свободы системы при эвтектической температуре и содержании компонента А 95%.

5. При какой температуре начнет отвердевать расплав, содержащий в% вещества А? При какой температуре он отвердеет полностью? Каков состав первых выпавших кристаллов?

6. Вычислите теплоты плавления веществ А и В.

Таблица 21

Вариант	Система	Состав А, мольн.%	T, К начала кристаллизации
1	2	3	4
1	A – KCl B – SnCl2	0 5 10 15 20 25 30 35 40 45 50 52,5 55 70 80 100	512 507 496 479 477 481 478 473 460 481 497 583 658 853 952 1050
2	A – KJ B – CdJ2	0 10 30 45 47 49 53 55 60 65 80 100	658 643 696 520 470 468 504 515 575 656 833 951

Продолжение таблицы 21

1	2	3	4
3	A – KCl B – MnCl2	0 8 15 25 34 36 38 40 50 60 65 66 75 85 100	923 825 865 715 745 722 735 747 769 731 705 701 705 925 1047
4	A – SrBr2 B – LiBr	0 5 20 30 34 40 50 60 66,6 85 100	825 813 772 736 720 744 768 773 803 865 916

Продолжение таблицы 21

1	2	3	4
5	A – MgSO4 B – Cs2SO4	0 10 20 30 40 45 47 50 55 60 63 65 70 80 90 100	1292 1241 1193 1116 1013 953 969 999 1048 1083 1098 1113 1163 1238 1323 1397
6	A – RbCl B – SrCl2	0 10 20 30 40 45 50 55 65 70 75 80 90 100	1147 1089 1004 906 964 975 978 968 896 827 853 879 960 999

Продолжение таблицы 21

1	2	3	4
7	A – KCl B – PbCl2	0 10 20 25 30 33,5 40 45 50 55 65 75 90 100	769 748 713 701 710 713 707 693 703 733 811 893 1003 1048
8	A – CsCl B – SrCl2	0 10 15 20 25 35 40 50 60 70 80 85 95 100	1147 1124 1089 1059 1102 1155 1166 1180 1158 1071 877 862 875,8 876,8

Продолжение таблицы 21

1	2	3	4
9	A – KCl B – CaCl2	0 10 20 25 31 35 45 50 55 65 75,5 77,5 80 85 89,5 90 95 100	1293 1216 1113 1069 953 963 1003 1011 1007 983 903 906 910 905 983 910 1055 1129
10	A – FeCl3 B – TlCl	0 10 22 26 29 33 35 37 45 52 62 100	702 658 598 535 549 563 525 506 533 553 572 575

Продолжение таблицы 21

1	2	3	4
11	A – CuCl2 B – CsCl	0 10 20 35 45 50 60 65 66,6 70 75 80 90 100	912 868 814 645 571 549 533 542 547 541 521 541 623 695
12	A – CdCl2 B – TlCl	0 10 20 28 30 36,5 47 50 57,5 67,5 80 85 95 100	702 656 604 572 589 645 694 699 697 673 754 777 823 841

Продолжение таблицы 21

1	2	3	4
13	A – SrBr2 B – LiBr	0 5 20 30 34 40 50 60 66,6 85 100	825 813 772 736 720 744 768 773 803 865 916
14	A – InCl3 B – NaCl	0 13,3 22,2 35,8 37,6 40 47 50,6 53 61,6 66,8 74,6 80,6 81,6 84,8 100	1073 1052 1033 989 975 983 999 1013 983 753 680 641 622 642 697 859
15	A – MgCl2 B – TlCl	0 5 15 28 33,3 50 66,6 75 90 100	708 698 682 635 685 767 796 658 950 951

Продолжение таблицы 21

1	2	3	4
16	A – SrBr2 B – KBr	0 10 25 29 33,3 40 50 57 66,7 75 82 85 95 100	1003 972 872 829 832 826 807 832 847 843 835 851 897 916
17	A – NiF2 B – KF	0 4,9 9,2 13,4 15,2 18,4 21,8 23,8 26 30,3 37,9 46,7 50,5 58	1121 1099 1060 1120 1141 1168 1193 1212 1224 1289 1359 1397 1403 1391

Продолжение таблицы 21

1	2	3	4
18	A – KJ B – KF	0 10 20 25 30 31 35 40 45 50 55 60 70 80 90 100	685 668 640 622 579 594 603 610 618 622 651 695 773 858 914 959
19	A – PbCl2 B – TlCl	0 10 15,5 20 25 30 36,5 40 50 60 66,6 70 75 80 90 100	708 679 661 675 680 676 650 658 680 705 708 707 700 720 752 773

Продолжение таблицы 21

1	2	3	4
20	A – MgSO4 B – K2SO4	0 10 20 30 40 50 63,9 66,8 71 75,3 82,2 100	1349 1308 1236 1123 1019 1103 1200 1203 1193 1177 1247 1397
21	A – MnCl2 B – RbCl	0 15 22 27 30 32 35 40 45 50 55 65 68 70 80 100	999 879 813 749 741 733 713 767 793 799 797 755 733 743 803 923

Продолжение таблицы 21

1	2	3	4
22	A – LiNO3 B – Pb(NO3)2	0 10 20 22 32,5 36 40 50 60 65 70 80 90 100	585 535,5 489 479 424 438 449,5 464 457,6 449 567 598 519,5 527
23	A – MnCl2 B – RbCl	0 17,5 22,7 23,7 25,9 28 29 30,4 33,1 35,5 36,2 37,5 43,8 50 58,1 65 68,3 78,7 100	991 868 800 764 746 736 732 743 749 745 759 784 816 823 809 783 821 989 984

Продолжение таблицы 21

1	2	3	4
24	A – Li2SO4 B – Cs2SO4	0 5 10 18,5 20 25 35 40 45 55 67 70 90 100	1043 1023 978 911 828 980 1022 1027 1015 961 873 899 1021 1049
25	A – HgBr2 B – HgJ2	0 10 20 30 40 50 55 60 65 70 80 90 100	528,4 518 509,2 500,8 494,1 490,3 489,3 489,1 489,6 490,8 495,2 501,9 509,5

Продолжение таблицы 21

1	2	3	4
26	A – Mg B – Cu	0 8 15 20 35 43 50 55 60 65 75 100	1085 680 800 750 550 590 550 500 450 380 500 645
27	A – Si B –Cr	0 10 20 25 30 40 50 60 70 80 90 100	2173 1823 1973 1993 1973 1873 1823 1703 1793 1673 1643 1693

Продолжение таблицы 21

1	2	3	4
28	A – Mg B –Ca	0 10 20 30 42 50 60 70 80 90 100	1081 973 718 923 994 981 931 873 791 873 913
29	A – KBr B – AgBr	0 10 20 30 40 50 60 70 80 90 100	683 643 553 543 628 723 823 863 903 973 1023
30	A – LiCl B – KCl	0 10 20 30 40 50 60 70 80 90 100	1046 1023 973 923 848 723 634 698 773 823 874

Таблица 22

Вариант	Т1, К	а, мол. %	б, мол. %	в, мол. %
1	483	45	75	5
2	723	55	75	10
3	873	40	80	10
4	873	50	80	10
5	1210	40	75	10
6	1173	55	90	10
7	1073	35	85	5
8	1100	30	75	5
9	1173	35	90	10
10	660	40	95	10
11	673	30	50	5
12	773	55	80	10
13	973	43	80	10
14	1033	60	90	10
15	923	45	95	100
16	933	50	80	10
17	1273	60	90	10
18	873	15	–	5
19	773	40	75	10
20	1273	85	10	10
21	873	50	90	10
22	523	30	95	10
23	883	40	75	10
24	1023	40	90	10
25	600	25	75	5
26	900	50	90	5
27	1200	60	90	10
28	1000	20	10	90
29	850	40	–	10
30	980	40	–	10

Решение:

Проанализируем диаграмму «температура–состав» для бинарной системы Li₂CO₃ – K₂CO₃ (табл. 23).

Построим диаграмму плавкости (рис. 5) – зависимость температуры кристаллизации от состава системы. Соединим точки на диаграмме линией (линия С G E₁ XC E₂ D). Это – линия ликвидуса. Точка максимума на ней (точка ХС) отвечает образованию устойчивого химического соединения. Точки минимума E₁ и E₂ – эвтектические точки. Эвтектикой называется смесь двух веществ, кристаллизующаяся при единой температуре.

Сделаем дополнительные построения: опустим перпендикуляр из точки ХС, проведем две горизонтальные линии через точки E₁ и E₂. Горизонтальные линии МE₁ и E₂N – линии солидуса.

Таблица 23

Система	Состав А, молярн.%	T, К начала кристаллизации
A – Li2CO3 B – K2CO3	0 9 20 33 39,5 44,2 50 54,5 62 66,6 83,5 100	1133 1060 955 733 765 778 788 778 765 798 911 983

Линии делят диаграмму на ряд областей. Выше линии ликвидуса любая смесь находится в жидком (расплавленном) состоянии. Ниже линии солидуса система находится в твердом состоянии и представляет из себя смесь кристаллов двух видов. В левой части диаграммы это смесь кристаллов вещества В (K₂CO₃) и кристаллов химического соединения. В правой части диаграммы - смесь кристаллов вещества А (Li₂CO₃) и кристаллов химического соединения. В заштрихованных областях в равновесии находятся жидкая и кристаллическая фазы.

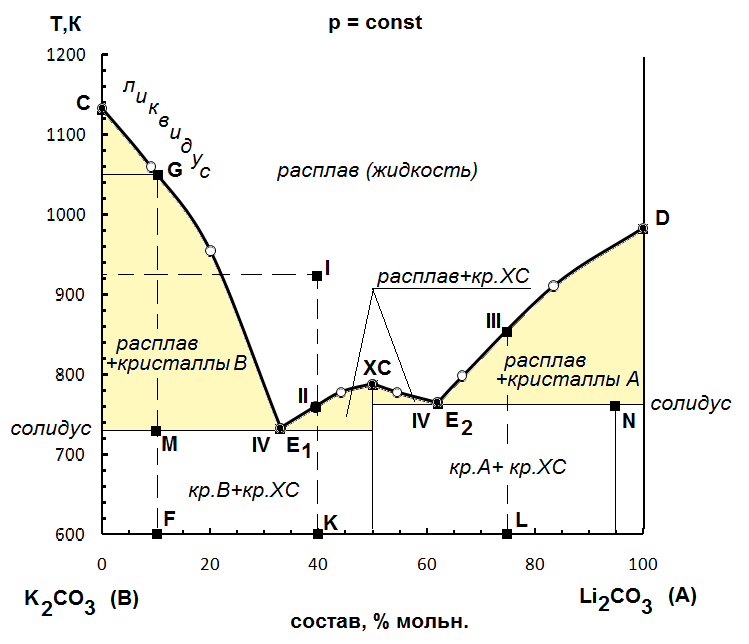
Рисунок 5 – Диаграмма плавкости для системы Li₂CO₃ – K₂CO₃

1. Обозначим точками:

I – жидкий плав, содержащий при температуре T₁ = 923К 40% Li₂CO₃. Для этого найдем на оси абсцисс точку, соответствующую составу 40% Li₂CO₃ – это точка К. На оси ординат отмечаем температуру T₁ = 923К. На пересечении линий получаем точку I, которая расположена в области выше линии ликвидуса, т.е. в области жидкого расплава;

II – плав, содержащий 40% Li₂CO₃, находящийся в равновесии с кристаллами химического соединения. Аналогичным образом найдем на оси абсцисс точку, соответствующую составу 40% Li₂CO₃ – это точка К. Восстановим перпендикуляр до пересечения с линией ликвидуса и получим точку II;

III – систему, состоящую из твердого Li₂CO₃ в равновесии с расплавом, содержащим 75% Li₂CO₃. Для этого найдем на оси абсцисс точку, соответствующую составу 75% Li₂CO₃ – это точка L. Восстановим перпендикуляр до пересечения с линией ликвидуса и получим точку III. На ветви ликвидуса DE₂ в твердую фазу переходит компонент системы Li₂CO₃; расплав при этом обогащается компонентом K₂CO₃.

IV – равновесие трех фаз. Равновесие трех фаз имеет место в точках эвтектики E₁ и E₂.

2. Определим составы химических соединений.

На представленной диаграмме одно химическое соединение (ХС), характеризующееся составом 50% компонента Li₂CO₃ и 50% компонента K₂CO_3.

3. Определим качественные и количественные составы эвтектик.

Качественный состав: твердые эвтектики состоят из кристаллов K₂CO₃ и кристаллов химического соединения (E1) и из кристаллов Li₂CO₃ и кристаллов химического соединения (E₂).

Количественный состав:

Е₁ – 33% Li₂CO₃ и 67% K₂CO_3.

Е₂ – 62% Li₂CO₃ и 38% K₂CO_3.

4. Определим по уравнению (68) число фаз и число термодинамических степеней свободы С системы при эвтектической температуре и 95% содержании компонента Li₂CO₃. При Т = 765 К (точка N) система трехфазна (Ф = 3) – в равновесии находятся две твердых фазы (кристаллы химического соединения и кристаллы K₂CO₃) и жидкий расплав; число компонентов К = 2, число внешних факторов n = 1, т.к. (p = const).Число степеней свободы

С_усл = 2 – 3 + 1 = 0.

Система безвариантна – в этой точке нельзя менять ни один параметр (температура, состав), не нарушив равновесия.

5. При какой температуре начнет отвердевать расплав, содержащий 10% Li₂CO₃? При какой температуре он отвердеет полностью? Каков состав первых выпавших кристаллов?

Для ответа на эти вопросы найдем на оси абсцисс точку, соответствующую составу 10% Li₂CO₃ – это точка F. Восстановим перпендикуляр до пересечения с линией ликвидуса в точке G, т.к. точки, лежащие на линии ликвидуса отвечают температуре начала кристаллизации. Для анализируемого состава получим температуру начала кристаллизации T = 1050 К. По линии GF осуществляется охлаждение расплава, содержащего 10% Li₂CO₃ до достижения линии солидуса в точке M. Расплав отвердеет полностью при эвтектической температуре T = 730 К. В процессе кристаллизации в твердую фазу переходит тот компонент, которого в системе больше (по сравнению с эвтектической точкой), на основании этого состав первых выпавших кристаллов – 100 % K₂CO₃.

6. Вычислим теплоты плавления веществ Li₂CO₃ и K₂CO₃.

Зависимость температуры кристаллизации расплава от состава расплава выражается уравнением Шредера:

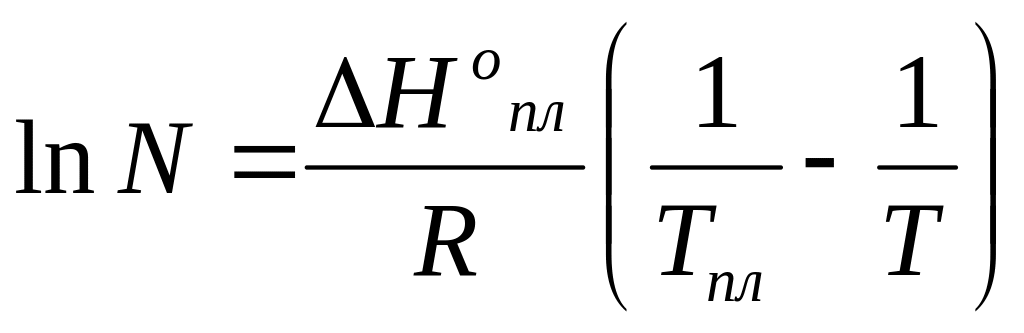, (69)

где N – мольная доля вещества в смеси;

– мольная теплота плавления чистого вещества;

– температура плавления чистого вещества;

T – температура начала кристаллизации расплава с мольной долей N.

Рассчитаем теплоту плавления вещества Li₂CO₃.

Для расчета возьмем сплав, содержащий 90% Li₂CO₃. Мольная доля Li₂CO₃ в системе = 0,9. Температура начала кристаллизации системы, содержащей 90% Li₂CO₃ T = 935 К. По диаграмме T_пл(Li₂CO₃) = 983 К (точка D).

По уравнению Шредера вычислим теплоту плавления вещества Li₂CO₃:

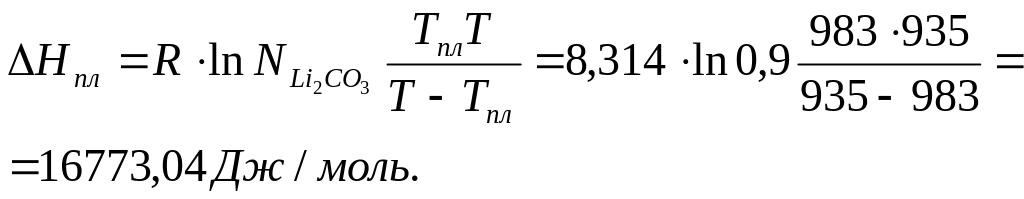
Теплота плавления Li₂CO₃ составила 16,8 кДж/моль.

Аналогичным образом рассчитаем теплоту плавления вещества K₂CO₃. Для расчета возьмем сплав, содержащий 90% K₂CO₃. Мольная доля K₂CO₃ в системе = 0,9. Температура начала кристаллизации системы, содержащей 90% K₂CO₃ T = 1050 К (см. пункт 5). По диаграмме T_пл(K₂CO₃) = 1133 К (точка C).

По уравнению Шредера вычислим теплоту плавления вещества K₂CO₃:

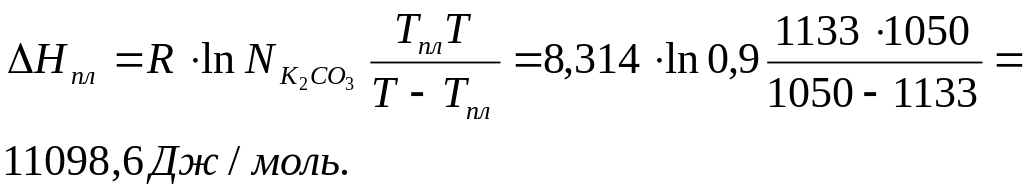
Теплота плавления K₂CO₃ составила 11,1 кДж/моль.

Контрольные вопросы

Тема 1. Расчет тепловых эффектов физических и химических превращений

1. Сформулируйте и объясните I закон термодинамики.

2. Поясните физический смысл величин, входящих в I закон термодинамики.

3. В чем заключается отличие теплоты и работы?

4. В чем отличие теплоты и работы от внутренней энергии?

5. Сформулируйте закон Гесса и его следствия. Для каких физико-химических процессов он применяется?

6. Дайте определение теплового эффекта химической реакции. Какие виды тепловых эффектов вы знаете?

7. Что такое внутренняя энергия, каковы ее общие свойства?

8. Сформулируйте понятие энтальпии реакции. Охарактеризуйте ее свойства.

9. Как связаны между собой энтальпия и внутренняя энергия?

10. Что такое стандартный тепловой эффект?

11. Дайте определение теплоты образования и теплоты сгорания.

12. Какие методы расчета тепловых эффектов при стандартных условиях вы знаете?

13. Как найти тепловой эффект реакции при стандартных условиях с помощью теплот образования и сгорания?

14. В чем заключается метод расчета тепловых эффектов при стандартных условиях по термохимическим уравнениям и схемам?

15. Как произвести расчет теплового эффекта реакции по энергиям химических связей?

Тема 2. Расчет тепловых эффектов физических и химических превращений при различных температурах

1. Дайте определение истинной теплоемкости.

2. Какие виды теплоемкостей вы знаете?

3. Запишите выражение для вычисления истинной теплоемкости при постоянном объеме или давлении.

4. Дайте определение удельной и молярной теплоемкости.

5. Напишите формулу для вычисления средней теплоемкости в интервале температур от Т₁ до Т₂.

6. Выразите взаимосвязь теплоемкости идеальных газов при постоянном давлении С_р и постоянном объеме С_v.

7. Является ли теплоемкость вещества функцией температуры?

8. Как рассчитать изменение теплоемкости в ходе реакции?

9. Каково влияние температуры на тепловой эффект реакции?

10. Запишите закон Кирхгофа в дифференциальной и интегральной формах. Проведите анализ уравнения.

11. Что такое температурный коэффициент реакции?

12. Как изменится тепловой эффект реакции с ростом температуры, если суммарная теплоемкость исходных веществ больше суммарной теплоемкости продуктов реакции и наоборот?

13. Что можно сказать о свойствах участников реакции, если тепловой эффект не зависит от температуры?

14. Проинтегрируйте уравнение Кирхгоффа для случаев приближенного расчета теплового эффекта при заданной температуре (∆С_p = 0, ∆С_p = const).

15. Используя зависимость теплоемкости участников реакции от температуры, проведите интегрирование уравнения Кирхгоффа для точного расчета теплового эффекта при заданной температуре.

Тема 3. Расчет характеристических термодинамических функций

1. Дайте определение абсолютной энтропии и укажите ее свойства.

2. Что такое стандартная энтропия вещества (S⁰₂₉₈)?

3. Как рассчитать изменение энтропии чистого вещества: а) при изменении температуры по данным о зависимости теплоемкости от температуры; б) при фазовых превращениях; в) для идеальных газов в различных процессах?

4. Почему для расчета изменения энтропии в необратимых процессах можно воспользоваться уравнениями, выведенными для обратимых процессов?

5. Как произвести расчет изменения энтропии химической реакции в стандартных условиях?

6. В каком случае изменение энтропии является критерием самопроизвольного протекания процесса?

7. Приведите формулу для расчета изменения энтропии химической реакции при различных температурах (∆С_p = const, ∆С_p = f (T)).

8. Дайте определение характеристической термодинамической функции.

9. Какая термодинамическая функция является критерием самопроизвольного протекания процесса при постоянных P и T? Каково значение этой функции в состоянии равновесия?

10. Какая термодинамическая функция является критерием самопроизвольного протекания процесса при постоянных V и T?

11. Каково соотношение между энергией Гиббса и энергией Гельмгольца для термодинамической системы?

12. Как произвести расчет изменения энергии Гиббса и Гельмгольца: а) через стандартные мольные функции Гиббса; б) по значениям ∆H⁰ и ∆S⁰.

13. Напишите уравнения зависимости энергий Гиббса и Гельмгольца от температуры и давления.

14. Укажите связь энергий Гиббса и Гельмгольца с полезной работой химических процессов.

15. Что такое химический потенциал? Как связаны между собой свободная энергия системы и химические потенциалы компонентов системы?