Лабораторная работа № 5 Определение модуля кручения и модуля сдвига с помощью крутильных колебаний.

Ц ель: 1) изучить крутильные колебания тонкого металлического стержня; 2) определить модуль кручения металлического стержня, используя метод крутильных колебаний; 3) определить модуль сдвига металлического стержня при крутильных колебаниях.

Оборудование: 1) установка ЛКМ – 7; 2) кронштейн для крепления испытуемого стержня к стойке установки; 3) кронштейн для крепления на испытуемом стержне тяжелой балки с отверстиями; 4) два тонких стержня в качестве образцов для экспериментов; 5) два массивных груза со штырями с креплениями к балке; 6) микрометр; 7) линейка.

Краткая теория.

В данной работе рассмотрим еще один вид неоднородной деформации более подробно - деформацию кручения металлического стержня и вызванные этим видом деформации твердого тела механические колебания. Однородный металлический стержень одним концом жестко прикреплен. К другому концу – прикладывается закручивающая сила, создающая крутящий момент каждого сечения стержня относительно продольной оси на угол φ. Такая деформация называется кручением. Как видно из рисунка 1 каждый бесконечно малый элемент проволоки АВСD перейдет в положение , что похоже на деформацию сдвига. Поэтому деформацию кручения возможно рассматривать как неоднородный сдвиг.

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и на изменяясь в размерах смещаются параллельно друг другу (рис.1).Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД , параллельная ВС, закреплена неподвижно. Так как угол мал, то формулу можно записать в виде:

, (1)

где СС₁ = x  абсолютный сдвиг,   угол сдвига, называемый также относительным сдвигом, измеряемый в радианах. Гуком экспериментально установлено, что при деформации сдвига относительный сдвиг  пропорционален касательному напряжению , то есть

, (2)

где S площадь поверхности грани ВС, N – коэффициент пропорциональности, называемый модулем сдвига. Выражая модуль сдвига из формулы (2) получим

(3)

данная формула позволяет сформулировать определение модуля сдвига, как физической величины, характеризующей касательное напряжение, которое возникло бы в образце при относительном сдвиге, равным 1 радиану (при условии, что закон Гука выполняется).

Таким образом, физические величины, характеризующие деформацию сдвига и деформацию кручения, должны быть связаны. При деформации кручения сила , под действием которой стержень испытывает данный вид деформации так, что его основание поворачивается по отношению к другому, фиксированному, на некоторый угол , создает момент сил . На основании закона Гука для деформации кручения, момент сил , пропорционален углу поворота одной плоскости относительно другой, фиксированной, то есть:

M = fφ, (4)

где f  модуль кручения данного стержня  физическая величина, характеризующая какой момент силы нужно приложить, чтобы закрутить стержень (твердое тело) на угол в 1 радиан. Таким образом, результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (см. рис. 2), причем

r=l (5)

С ледовательно, расчет деформации кручения может быть сведен к деформации сдвига. Приведем без вывода соотношение, существующее между модулем кручения f и модулем сдвига N материала стержня:

, (6)

где d – диаметр стержня, l – его длина.

Из формулы (6) видно, что модуль кручения зависит не только от материала, но от геометрических размеров проволоки, и может быть экспериментально определен, наблюдая крутильные колебания. В качестве крутильного маятника может служить рейка с закрепленными на нее цилиндрическими грузами массами m. В соответствии с основным законом динамики вращательно движения

(7)

где M  момент сил, определяемый по закону Гука для деформации кручения (4), J – суммарный момент инерции грузов, треугольного кронштейна и балки (J = mr² + J_б +J_кр),  – угловое ускорение равное по определению второй производной угла поворота по времени

. (8)

Подставляя (8) и (4) в формулу (7) получим:

(9)

Разделив обе части уравнения (5) на J.

Обозначим как , (10)

получим выражения следующего вида:

. (11)

Данное выражение является дифференциальным уравнением гармонических колебаний крутильного маятника. Как уже говорилось во введении и в предыдущих лабораторных работах решением такого уравнения является выражение

 = Аcos t.

Формула (10) позволяет сделать вывод, что период колебании такого маятника может быть вычислен следующим образом:

(12)

Чтобы найти f, необходимо исключить неизвестный момент инерции J. Для этого в эксперименте определяются два периода колебаний крутильного маятника. Используя возможность передвижения грузов на рейке установки, меняем расстояние от оси вращения. В соответствии с l₁, l₂ получаем моменты инерции J₁, J₂:

J₁ = J₀ + 2ml₁²

(13)

J₂ = J₀ + 2ml₂²,

Где J₀  момент инерции рейки крутильного маятника. Периоды колебаний будут соответственно равны

(14)

подставляя выражения (13) в (14), получим

.

Решая совместно два последних уравнения, получаем формулу для расчета модуля кручения стержня крутильного маятника

(15)

Очевидно график зависимости T²(l²) будет линейным, так как l² - единственная в правой части уравнения изменяющаяся величина. Поэтому тангенс угла наклона  графика к оси l² будет равен , откуда

, (16)

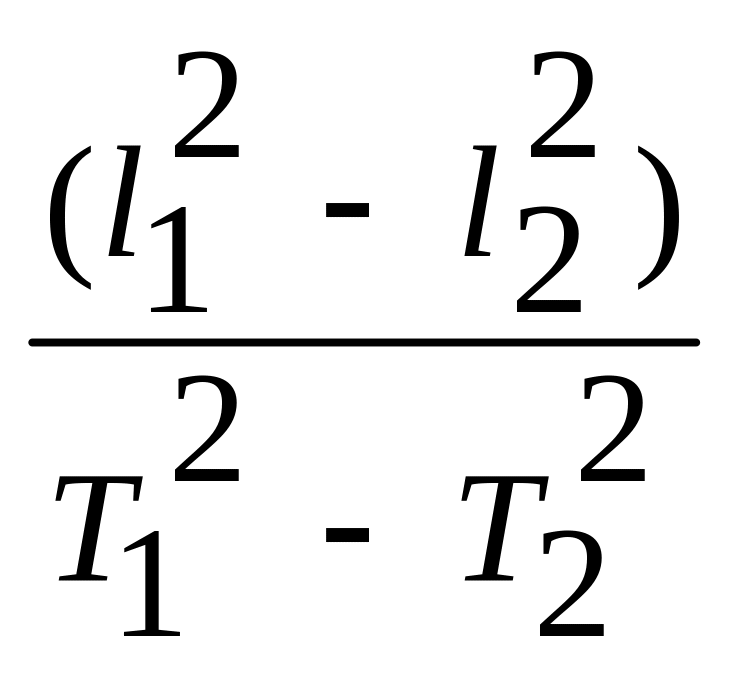где tg = . (17)

Используя формулу (6), по модулю кручения f возможно засчитать модуль сдвига N.