16. В чем состоит формула Эйлера и для каких объектов она верна?

• Грань плоского графа – часть плоскости ограниченная его ребрами и не содержащая в себе ни ребер, ни вершин.

• Теорема: для любого плоского связного графа В + Г – Р = 2 – формула Эйлера.

17. Как выглядят непланарные графы №1 и №2, типов 1 и 2, в чем состоит теорема Куратовского-Понтрягина? + задача

• 

• 

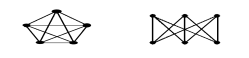
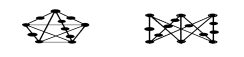
• Теорема: граф планарен тогда и только тогда, когда он не содержит в себе графов типа 1 и типа 2.

18. Что такое хроматическое число графа и что вы знаете о его величине? + задача

• Наименьшее число n, при котором существует правильная n-цветная раскраска данного графа, называется его хроматическим числом.

• Если максимальная степень вершины равна d, то его хроматическое число hB<=d+1, если граф являеться полным (d=4, hB=5) или d=2, при этом граф содержит цикл нечетной длины.

• В остальных случаях hB<=d.

19. Что такое хроматический индекс графа и что вы знаете о его величине? + задача

• Минимальное число цветов, необходимое для правильной раскраски ребер называется храматическим индексом и обозначается hP

• Обозначим через d максимальную степень вершин графов. Все ребра инцидентные одной вершине должны иметь разные цвета. Отсюда hP >= d

• Для любого графа верно:

• d <= hP <= d+1. Т.е. либо hP = d, либо hP = d + 1.

20. Что такое матрица смежности орграфа и каким свойством обладает матрица смежности неориентированного графа?

• Пусть дан орграф с n-пронумерованными вершинами. Матрица A размера nхn, заполняется числами:

aij =

21. Как строится код Харари? + задача

• Пусть дан неориентированный граф.

• Расположим его в виде двоичной строки (слева на право и сверху вниз)

• Меняя нумерацию вершин графа, точно так же получим другие двоичные строки (числа).

• Сравним их между собой именно как числа (по первому виду).

• Наибольшее из полученных чисел и есть код Харари, а нумерация вершин, давшая это число – называется канонической.

22. Что называется деревом, ордеревом и как они связаны между собой? + задача

• Связный граф, не имеющий циклов называется деревом.

• Орграф называется ордеревом, если:

- существует особая вершина (корень ордерева) в которую не входит ни одна дуга.

- во все остальные вершины входит единственная дуга.

• Свойства графов эквивалентности:

- граф явлется деревом.

- граф связен и Р = В – 1

- граф не имеет циклов и Р =В – 1

- граф связен, но утрачивает связность при удалении любого ребра (вершины остаются)

- граф не имеет цикла, но при добавлении любого нового ребра (но не вершин) циклы появляються.

23. Как строится префиксный код бинарного ордерева? + задача

• Каждой вершине ордерева (кроме корня) мы сопоставляем двоичное число.

• Левому потомку корня 0, правому 1.

• Потомкам 00 – 00 и 01, потомкам 1 – 10 и 11 соответственно и т.д.

24. Как строится код Прюфера? + задача

• Пусть имеется дерево с n-пронумерованными вершинами.

• В списке всех вершин 1, 2, 3…n слева на право ищем первую висячую вершину.

• Пусть это a₁, ищем единственную вершину b₁, с которой смежна a₁.

• Вершину b₁ заносим в новый список – будущий код Прюфера, а вершину a₁ вычеркиваем и из списка и из дерева.

• Этот процесс проверяем n-2 раза.

• В результате получаем новый список {b₁, b₂…b_n-2} – это и будет код Прюфера.

25. Какие три способа обхода бинарного дерева вы знаете? + пример с более 10 вершинами + задача

• Прямой метод (КЛП): обойти корень, затем левое поддерево, затем правое поддерево.

• Обратный метод (ЛКП): обойти левое поддерево, корень, правое поддерево.

• Концевой метод (ЛПК): обойти левое поддерево, правое поддерево, корень.