Векторное изображение синусоидальных величин.
При
гармоническом изменении синусоидальной
величины постоянной остаётся амплитуда.
Этим можно воспользоваться для определения
мгновенного значения электрической
величины, не рассматривая графика её
зависимости от времени.
Синусоидальную
функцию времени можно изобразить
вектором, равным амплитуде данной
функции, равномерно вращающимся с
угловой скоростью ω.
При этом начальное положение вектора
определяется (для t=0)
его начальной фазой
.
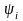На
рис. 3.3 показаны вращающийся вектор тока
и график изменения тока
во времени.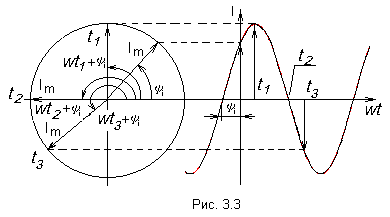
При
изображении синусоидальной ЭДС,
напряжений и токов из начала координат
проводят векторы, равные амплитудным
значениям этих величин, под углом
к горизонтальной оси. Положительные
углы
откладываются против часовой стрелки.
Если
вращать вектор против часовой стрелки,
то в любой момент времени он составит
с горизонтальной осью угол, равный
.
Проекция вращающегося вектора на ось
ординат (ось мгновенных значений) равна
мгновенному значению синусоидальной
величины.
Совокупность векторов на
плоскости, изображающих Э.Д.С., напряжения,
токи одной частоты, называют векторной
диаграммой.
При исследовании
установившихся режимов векторы
неподвижны, их длина равна действующим
значениям электрических величин.
С
помощью векторов можно производить
геометрическое суммирование электрических
величин.
Т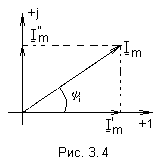
ак,
на рис. 3.4 показаны векторы токов
и
,
а также вектор их геометрической суммы
.
Углы
обозначают начальные фазы токов.
Векторные диаграммы широко используются при анализе электрических цепей переменного тока.
14. Действующее и среднее значение синусоидального тока, напряжения и эдс.
15. Символическое изображение синусоидальной функции. Использование комплексных чисел для замены действий с синусоидальными функциями.
Вращающемуся
вектору на комплексной плоскости
соответствует комплексное число с
постоянным модулем и переменным
аргументом, например
(для вектора, изображающего синусоидальное
напряжение). Такое комплексное чисто
называют символическим изображением
синусоидальной функции или ее комплексным
мгновенным значением. Представим его
в алгебраической форме (6):
.(6)
Получаем: синусоидальная функция (в некоторых учебниках ее при этом называют оригиналом) может быть определена как мнимая часть ее символического изображения, взятая без j,
В целях сокращения записи рассмотренных соотношений используется знак Û, который читается "соответствует" или "изображает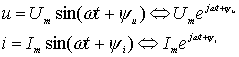" (7):
(7)
Знак Û может быть поставлен также между комплексной амплитудой и синусоидальной функцией (8);
(8)
Представление синусоидальных величин комплексными числами.
Синусоидально изменяющуюся электрическую величину можно представить комплексным числом и изобразить в виде вектора на комплексной плоскости с прямоугольной системой координат.
Комплексное число состоит из действительной (вещественной) и мнимой частей. По оси ординат откладывают мнимую часть комплексного числа, а ось обозначают +j; по оси абсцисс – действительную часть комплексного числа, а ось обозначают +1.
На комплексной плоскости синусоидальная величина может изображаться в виде модуля и аргумента или в виде двух составляющих вектора, направленных по действительной и мнимой осям.
Н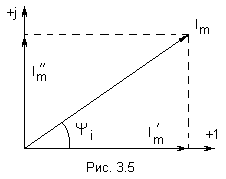
апример,
синусоидальный ток
представляют вектором
,
модулем которого является значение
амплитуды тока
,
а аргументом – начальная фаза
,
которую можно выражать в радианах или
в градусах (рис. 3.5).
Составляющим
вектора
по действительной оси будет
,
а по мнимой -
,
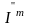то есть
.
Вектор называют комплексной амплитудой тока.
Обычно при расчётах пользуются действующими значениями.
При построении векторных диаграмм точно фиксируют угол сдвига между векторами, а положение их относительно осей комплексной плоскости может быть произвольным, поэтому оси можно не изображать.
При анализе электрических цепей переменного тока приходится иметь дело с умножением и делением электрических величин. В этом случае удобно пользоваться комплексами этих величин, записанными в показательной форме:
,
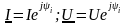где
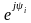- оператор поворота единичного вектора
относительно оси действительных величин.
Например, при
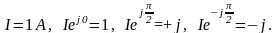
Умножение на j означает поворот вектора на +90 градусов (в сторону, противоположную направлению движения стрелки часов).
Умножение на –j означает поворот вектора на угол –90 градусов (по часовой стрелке).