11. Преобразование электрических схем. Параллельное и последовательное соединения. Преобразование треугольника в звезду.

Соединение трех сопротивлений, имеющее вид трехлучевой звезды, называют звездой, а соединение трёх сопротивлений так, что они образуют собой стороны треугольника - треугольником

В узлах 1, 2, 3 (потенциалы их ) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).

Обозначим токи, подтекающие к узлам 1, 2, 3, через I₁ I₂ I₃ . Часто при расчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноимённых точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема вне заметит произведенной замены. Выведем формулы преобразований. С этой целью выразим токи I₁ I₂ I₃ в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

Для звезды

Но

Подставим эти 4 уравнения и найдём

Введём в выражение с токами….для тока I₁

Для треугольника в соответствии с обозначениями:

Так как ток I₁ , в схеме должен равняться току I₁ в схеме при любых значениях потенциалов , то коэффициент при в правой части последнего уравнения должен равняться коэффициенту при в правой части предпоследнего уравнения , а коэффициент при в правой части последнего уравнения должен равняться коэффициенту при в правой части предпоследнего уравнения. Следовательно.

Последние 3 формулы дают возможность найти проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе-сумма проводимостей лучей звезды.

Из уравнений выразим сопротивления лучей звезды через сопротивления сторон треугольника:

1 2. Передача энергии от активного двухполюсника нагрузке

13. Цепи синусоидального тока. Синусоидальный ток. Основные параметры (амплитуда, угловая частота, начальная фаза). Представление синусоидальной функции в виде вращающегося вектора.

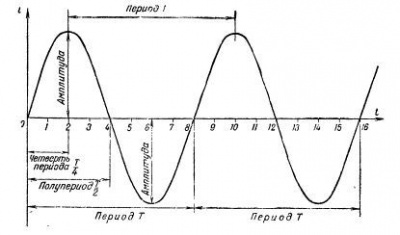
Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону (рис):

Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают .

Период – это время, за которое совершается одно полное колебание.

Частота равна числу колебаний в секунду , единица частоты - герц (Гц).

Угловая частота , единица угловой частоты рад/с или .

Аргумент синуса, т.е. , называют фазой. Фаза характеризует состояние колебания в данный момент времени .

Начальная фаза тока - .

Любая синусоидальная функция характеризуется тремя величинами: амплитудой, угловой частотой и начальной фазой.

Синусоидальные токи и ЭДС сравнительно низких частот, до нескольких килогерц, получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых и полупроводниковых генераторов, подробно рассматриваемых в разделе – электроника.