21. Определение резонанса и общий подход к анализу резонансных явлений.

Рассмотрим цепь с двумя параллельными ветвями на рис. 3.22.

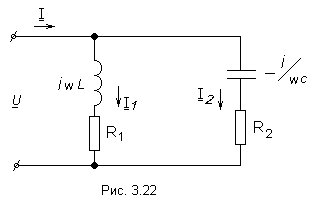
Такую цепь часто называют параллельным контуром. Условием возникновения резонанса является равенство реактивных проводимостей:

, (3.57) . (3.58) (3.59)

При противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил название резонанса токов.

22.Резонанс напряжений. Характеристики, добротность, затухание, волновое характеристическое сопротивление.

23. Резонанс токов. Коэффициент мощности и пути его повышения.

Р ассмотрим цепь с двумя параллельными ветвями на рис. 3.22.

Такую цепь часто называют параллельным контуром. Условием возникновения резонанса является равенство реактивных проводимостей:

, (3.57)

. (3.58)

. (3.59)

П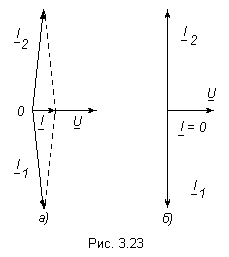 ри противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в рассматриваемой цепи получил названи резонанса токов.

Из векторной диаграммы на рис. 3.23а видно, что при резонансе ток на выходных выводах контура может быть значительно меньше токов в отдельных ветвях.

При резонансе общий ток в параллельном контуре по фазе совпадает с приложенным напряжением.

Добротность контура показывает, во сколько раз ток в ветви превышает питающий ток и определяется следующим соотношением:

, (3.60) где ,

- эквивалентное активное сопротивление при резонансе:

- если . (3.61)

В общем случае резонансная частота определяется по формуле:

, (3.62)

где - резонансная угловая частота при

. (3.47)

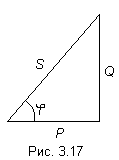
Графически эту связь можно представить в виде прямоугольного треугольника (рис. 3.17) – треугольника мощности, у которого имеются катет, равный Р, катет равный Q и гипотенуза S.

Отношение Р к S, равное , называется коэффициентом мощности.

. (3.48)

На практике всегда стремятся увеличить , так как реактивная мощность, которая всегда существует в цепи R, L, C, не потребляется, а используется лишь активная. Из этого можно сделать вывод, что реактивная мощность является лишней и ненужной.

24. Энергетические соотношения при резонансе, практическое применение резонансов.

25. Выражение синусоидального тока в комплексной форме записи.

Синусоидально изменяющуюся электрическую величину можно представить комплексным числом и изобразить в виде вектора на комплексной плоскости с прямоугольной системой координат. Комплексное число состоит из действительной (вещественной) и мнимой частей. По оси ординат откладывают мнимую часть комплексного числа, а ось обозначают +j; по оси абсцисс – действительную часть комплексного числа, а ось обозначают +1. Н а комплексной плоскости синусоидальная величина может изображаться в виде модуля и аргумента или в виде двух составляющих вектора, направленных по действительной и мнимой осям. Например, синусоидальный ток представляют вектором , модулем которого является значение амплитуды тока , а аргументом – начальная фаза , которую можно выражать в радианах или в градусах (рис. 3.5). Составляющим вектора по действительной оси будет , а по мнимой - , то есть Вектор называют комплексной амплитудой тока. При построении векторных диаграмм точно фиксируют угол сдвига между векторами, а положение их относительно осей комплексной плоскости может быть произвольным, поэтому оси можно не изображать. При анализе электрических цепей переменного тока приходится иметь дело с умножением и делением электрических величин.

В этом случае удобно пользоваться комплексами этих величин, записанными в показательной форме: где - оператор поворота единичного вектора относительно оси действительных величин Умножение на j означает поворот вектора на +90 градусов (против часов стрелки). Умножение на –j означает поворот вектора на угол –90 градусов (по часовой стрелке).