Векторные и топографические диаграммы

Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.

Д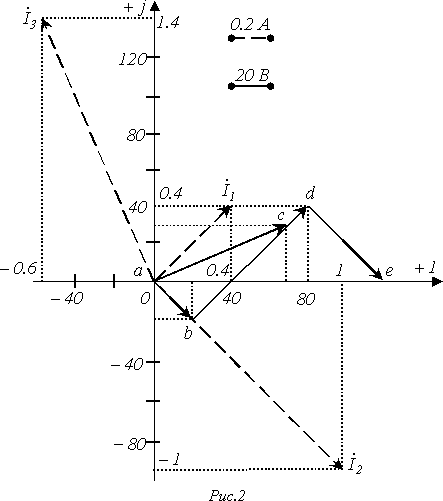 ля наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.

При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.

18. Токи и напряжения при параллельном соединении r, l, с. Треугольники токов и проводимостей. Токи и напряжения при параллельном соединении r, l, с.

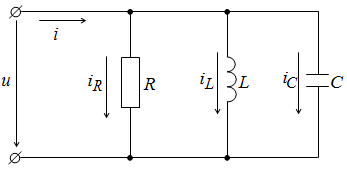
Пусть к цепи (рис. 2.12) приложено напряжение . По первому закону Кирхгофа

Ток в резисторе R совпадает по фазе с напряжением u, ток iL отстает, а ток iC опережает напряжение на угол φ = p / 2. Следовательно, суммарный ток равен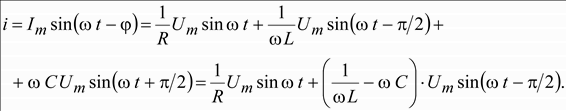

Рис. 2.12. Схема параллельного соединения R, L, C

Это тригонометрическая форма записи I закона Кирхгофа. Величина называется реактивной проводимостью цепи и может иметь индуктивный (B > 0) или емкостной (B < 0) характер.

В комплексной форме уравнение (2.29) имеет вид

Или

Отношение называется комплексной проводимостью.

Действительная часть полной проводимости G называется активной проводимостью, а мнимая B – реактивной. Векторная диаграмма на рис. 2.13 строится по уравнению (2.30). Треугольники токов и проводимостей.

Прямоугольный треугольник с катетами IR и (IL + IC) и гипотенузой I называется треугольником токов. Модуль полного тока равен

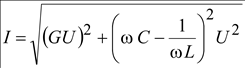или

где

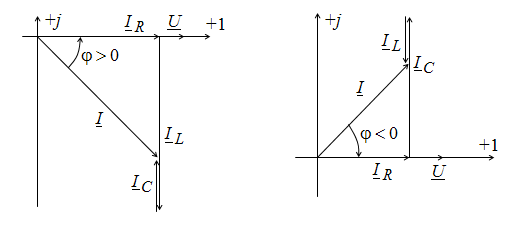Рис. 2.13. Векторная диаграмма напряжения и токов при параллельном соединении элементов

Угол сдвига фаз:

Если задано напряжение u = Um sin(ω t + y), то ток в исследуемой цепи равен i = Y Um sin (ωt + y – φ). (2.33)

При BL = BC (B = 0) реактивная составляющая тока равна нулю. Такой режим называется резонансом токов. Он характерен малым током, который потребляется от источника. Активная, реактивная и полная проводимости образуют треугольник проводимостей (рис. 2.14). Из его рассмотрения следует G = Y cos φ, B = Y sin φ. Помножив стороны треугольника на напряжение, получим треугольник токов со сторонами Iа = GU = Y cos φ U = I cos φ; Iр = BU = Y sin φ U = I sin φ;

Т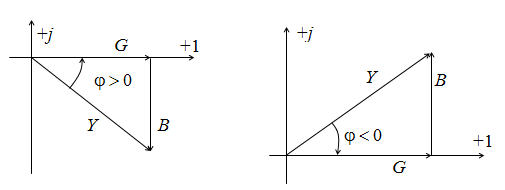 реугольник проводимостей