8. Среднее значение функции

Пусть дана функция и на интервале построен

её график (рис. 8.1). Площадь фигуры будет равна (а)

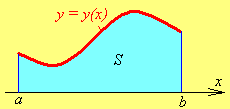
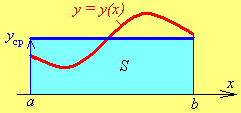
Рис. 8.1 Рис. 8.2

Выровняем верхнюю границу фигуры, сохранив её площадь (рис. 8.2). Получится прямоугольник, площадь которого (б)

Приравняв правые части формул (а), (б), получим

Формула вычисления среднего значения функции на интервале .

(8.1)

З а д а ч а 1. Найдите среднее значение функции при

□

■

З а д а ч а 2. По проводнику с сопротивлением течёт переменный электрический ток ( амплитуда, круговая частота колебаний тока). Найдите среднее значение мощности тока. (Справка. Используйте полученный в физике результат: мгновенное значение мощности электрического тока определяется по формуле

□ Подставим значение в формулу мощности: Так как то Теперь находим среднее значение мощности тока за произвольный промежуток времени

(а)

Покажем, что а потому член можно отбросить. Для технических целей применяется переменный ток частотой 50 Гц. В этом случае круговая частота Отсюда

Обычное время наблюдения человека за мощностью тока намного превышает крошечную величину поэтому эту величину действительно можно отбросить. Тогда из (а) получим

■

Тренировка по теме «Среднее значение функции»

Решите задачи.

а) Вычислите среднее значение функции на интервале [1, 8].

1) 2) 3) 4) 5)

б) Вычислите среднее значение функций и на интервале

1) и 2) и 3) и 4) и 5) и