5. Свойства определённого интеграла
При вычислении, исследовании определённого интеграла могут пригодиться следующие свойства определённого интеграла:
|
Переменную интегрирования можно обозначать любой буквой. |
(5.1) |
|
Если переставить пределы интегрирования, интеграл умножится на -1. |
(5.2) |
|
Интеграл от суммы (разности) равен сумме (разности) интегралов.
|
(5.3) |
|
Постоянный множитель можно вынести за знак интеграла. |
(5.4) |
|
Свойство аддитивности, или сложения. |
(5.5) |
|
(5.6) |
|
Свойства (5.1) – (5.5) вытекают из соответствующих свойств знака двойной подстановки. В качестве примера докажем формулу (5.5):
=
(3.6) =
Докажем равенства (5.6). Если – чётная функция (рис. 5.1), то
=│Фигура
симметрична относительно оси
│=
Если же – нечётная функция (рис. 5.2), то
=│Фигура
симметрична относительно точки
│=
■
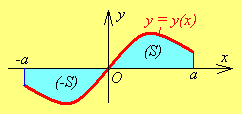
Рис. 5.1 Рис. 5.2
Примеры:
Тренировка по теме «Свойства определённого интеграла»
Найдите интегралы.
1)
2)
3)
4)
5)
1)
2)
3)
4)
5)
1)
2)
3)
4)
5)
1)
2)
3)
4)
5)
1)
2)
3)
4)
5)
6. Вычисление определённого интеграла с помощью замены переменной
|
=
=│Сделаем
замену
или
│=
=
■
З
а д а ч а 1. Найдите
□
=
=
■
Тренировка по теме
«Вычисление определённого интеграла с помощью замены переменной»
Найдите интегралы.
1)
2)
3)
4)
5)
№
9.1.47.
1)
2)
3)
4)
5)
№
9.1.48.
1)
2)
3)
4)
5)
7. Частичное интегрирование в определённом интеграле
Частичное интегрирование (или интегрирование по частям) ведётся по формуле
|
(7.1)
которую можно записать в виде
Применив к формуле (5.1-1) формулу (4.1), сразу получим (7.1). ■
З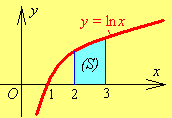
а д а ч а 1. Найдите площадь криволинейной
трапеции, ограниченной линией
осью
и прямыми
.
□
Нарисуем
фигуру
(рис.7.1) и вычислим её пло-
щадь:
=
■ Рис.
7.1
Тренировка по теме «Частичное интегрирование в неопределённом интеграле»
Найдите интегралы.
1)
2)
3)
4)
5)
1)
2)
3)
4)
5)
