26. Круговая поляризация электромагнитных волн.

Для получения случая линейной поляризации необходимо, чтобы составляющие вектора были синфазными или противофазными.

Рассмотрим второй частный случай. Пусть амплитуды составляющих и равны, а начальные фазы отличаются на :

,

Тогда

,

Подставляя эти значения в выражение для угла , получим:

,

откуда следует, что

,

Величина вектора при этом остается неизменной:

.

Таким образом, в фиксированной точке пространства вектор , оставаясь неизменным по величине, вращается с угловой частотой вокруг направления оси 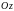. Конец вектора при этом описывает окружность. Волны такого типа называются волнами с круговой поляризацией.

27. Граничные условия для нормальных компонент векторов е и d

Рассмотренный выше простейший вид электромагнитного волнового процесса − плоская волны − является весьма идеализированным, поскольку здесь предполагается бесконечная протяженность волновых фронтов. В любой практической задаче электромагнитное поле тем или иным способом ограничено в пространстве. Естественными границами могут быть, например, металлические стенки волновода или границы раздела между средами с различными параметрами. Если параметры сред на границе раздела изменяются скачкообразно, то в общем случае компоненты векторов электромагнитного поля также претерпевают разрыв в точках границы. Далее мы найдем связи между векторами поля на границе, которые удовлетворяли бы уравнениям Максвелла.

Математическая постановка данной задачи выглядит следующим образом. Предположим, что две среды с номерами 1 и 2 разделены поверхностью . Вблизи от границы раздела известно полное электромагнитное поле, относящееся к области 1. Требуется отыскать электромагнитное поле в такой же окрестности, принадлежащей области 2.

Среда 1 имеет параметры , , 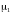, среда 2 − соответственно , , 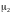. Поскольку на границе эти параметры меняются скачкообразно, то надо ожидать, что компоненты векторов поля при переходе границ раздела сред также будут испытывать разрывы. Тогда векторная линия будет претерпевать излом.

Для упрощения решения поставленной задачи векторы электромагнитного поля, рассматриваемые на границе раздела сред, принято разлагать на тангенциальные (касательные) и нормальные составляющие.

Методика вывода граничных условий и соответствующая иллюстрация остаются здесь совершенно аналогичными тем, что были использованы при выводе условий для нормальных составляющих магнитного поля. Однако за основу принимается не четвертое уравнение Максвелла , а третье . Отсюда возможны два случая.

Первый. Плотность поверхностных электрических зарядов равна нулю. Суммарный электрический заряд , заключенный внутри малой цилиндрической области, при этом равен нулю. В соответствии с теоремой Гаусса

,

откуда по аналогии с предыдущим выводом следует

.

Итак, при отсутствии поверхностных электрических зарядов нормальные составляющие векторов электрического смещения на границе раздела двух сред непрерывны, в то время как нормальные составляющие напряженностей электрического поля в общем случае претерпевают скачок:

.

Второй случай. На границе раздела равномерно распределен поверхностный электрический заряд с плотностью .

В этом случае, очевидно, стремление к нулю высоты цилиндра 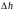не влияет на величину заряда, заключенного внутри цилиндра. Воспользовавшись законом Гаусса, можно записать формулу:

,

откуда следует

.

Это выражение означает, что при наличии заряженной границы раздела нормальные составляющие векторов электрической индукции испытывают скачок, по величине равный плотности поверхностного заряда в исследуемой точке. Физически это обусловлено тем, что заряд, расположенный на поверхности, создает свое собственное поле, ориентированное таким образом, что по одну сторону от границы раздела это поле складывается со внешним полем, а по другую вычитается.