9. Классификация сред

В зависимости от свойств параметров , и среды подразделяются на линейные и нелинейные.

Линейные среды – среды, в которых параметры , и не зависят от величин и направлений электрического и магнитного полей; в этом случае зависимости , являются линейными.

Нелинейные среды – среды, в которых параметры , , , или хотя бы один из них, зависят от величины электрического или магнитного полей. В этом случае соотношения , оказываются нелинейными функциями.

Линейные среды, в свою очередь, делятся на неоднородные и однородные, изотропные и неизотропные.

Однородными называют среды, параметры которых , , не зависят от координат, т.е., одинаковы во всех точках рассматриваемой среды.

Неоднородными называют среды, у которых хотя бы один из параметров , , является функцией пространственных координат: , , .

Изотропными называют среды, электромагнитные свойства которых одинаковы по всем направлениям, т.е. не зависят от направления векторов внешнего поля. Для изотропных сред параметры , , являются скалярами, а векторы и , и параллельны друг другу.

10. Тензоры диэлектрической и магнитной проницаемости

Существует ряд сред, свойства которых существенно зависят от направления векторов внешнего электромагнитного поля. Такие среды называют анизотропными. В них пары векторов и , и могут быть непараллельными и, по крайней мере, один из параметров , , является тензором.

Например, вектор направлен по оси , т.е., имеет одну составляющую , а вектор не совпадает по направлению с вектором и имеет все три составляющие: , , (рисунок Error: Reference source not found). Каждая из составляющих вектора пропорциональна вектору с разными коэффициентами пропорциональности :

, , .

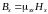В общем случае каждая проекция вектора на оси координат зависит от всех трех составляющих вектора , связь между ними определяется системой уравнений:

Таким образом, параметр анизотропной ферромагнитной среды характеризуется девятью коэффициентами, записываемыми в виде матрицы − тензора:

.

В этом случае векторы и связаны соотношением

.

Аналогично для анизотропного диэлектрика

,

где − тензор диэлектрической проницаемости.

11. Закон полного тока (закон Ампера)

Рассмотрим в пространстве воображаемый контур , ограничивающий поверхность . Зададим на этом контуре направление обхода так, чтобы движение вдоль контура с конца вектора элементарной площадки наблюдалось в направлении против часовой стрелки. Предположим далее, что поверхность пронизывается векторным полем токов, распределенных в пространстве с некоторой плотностью . Тогда полный ток, пронизывающий контур, определится как поток вектора плотности тока через поверхность в виде

,

где − вектор плотности тока проводимости, − поверхность, ограниченная контуром .

Закон полного тока гласит, что циркуляция по контуру вектора напряженности магнитного поля, вызванного протеканием тока , равна полному току:

,

.

Физический смысл этой формулы заключается в том, что при перемещении электрических зарядов, выражающемся в появлении электрического тока, появляется магнитное поле.