51. Элементарный электрический излучатель. Векторный электрический потенциал

Пользуясь результатами рассмотрения электродинамических потенциалов, вычислим поле векторного электрического потенциала, возбуждаемого элементарным электрическим излучателем в неограниченном свободном пространстве ( , ).

В соответствии с физической постановкой данной задачи воспользуемся сферической системой координат , в начальной точке которой расположим излучатель. Ввиду малости геометрических размеров излучателя радиус-вектор , входящий в формулу для электродинамического потенциала , может считаться постоянным и равным сферической координате . Отсюда будем иметь

.

Интегрирование вектора плотности стороннего тока по объему, занятому излучателем, представляет, на первый взгляд, логические трудности, поскольку, по определению, объем излучателя должен быть устремлен к нулю. Наиболее простой путь состоит в анализе физической размерности интеграла, входящего в последнюю формулу. Нетрудно проверить, что данный интеграл имеет размерность . Здесь известны амплитуда стороннего электрического тока в излучателе и его длина .

Требуемая размерность будет получена, если положить , откуда

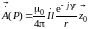
Единичный вектор i в двух последних формулах указывает на то, что ось элементарного излучателя направлена параллельно оси .

Для дальнейшего анализа необходимо знать разложение вектора 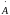в каждой точке пространства по ортам сферической системы координат.

,

.

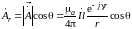Поскольку вектор электрического потенциала всюду направлен параллельно оси , его проекция на направление азимутального угла тождественно равна нулю, т.е. .

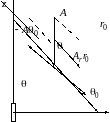
Определение сферических проекций векторного потенциала

52. Элементарный электрический излучатель. Диаграмма направленности

Диаграммой направленности произвольной антенны называется зависимость амплитуд векторов поля в дальней зоне от угла наблюдения.

В случае элементарного электрического излучателя диаграмма направленности описывается функцией 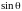. Это значит, что излучение энергии в направлении оси излучателя отсутствует; максимальное излучение происходит при , т. е. в экваториальной плоскости излучателя.

Нормированная диаграмма направленности элементарного излучателя

Как правило, на практике пользуются нормированными диаграммами направленности, при этом по оси ординат откладывается величина напряженности поля при данном угле наблюдения, отнесенная к максимальному значению напряженности. Нормированная диаграмма направленности элементарного излучателя представляет собой отрезок синусоиды на интервале от до .

Весьма наглядным является представление нормированной диаграммы направленности в полярной системе координат. Принцип полярной диаграммы заключается в том, что здесь на каждом луче, проведенном из начала координат под заданным углом 0, откладывается нормированная величина напряженности поля. Нетрудно убедиться, что в случае элементарного электрического излучателя геометрическим местом точек диаграммы направленности будет окружность, поскольку

.

Несмотря на то, что физически областью изменения углов является интервал , часто диаграмму направленности изображают в обеих полуплоскостях, подчеркивая этим, что излучение вибратора равномерно (изотропно) по всем углам. Именно таким образом построена диаграмма направленности на данном рисунке.

Построение диаграммы направленности элементарного электрического излучателя в полярной системе координат.