42. Основная волна н10 в прямоугольном волноводе

Начнем с построения качественной картины поля. При этом в качестве исходной можно использовать структуру поля волны в волноводе, образованиом двумя идеально проводящими плоскостями.

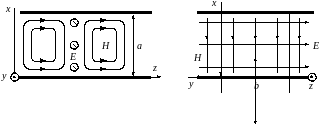
Построение картины распределения электромагнитного поля типа

Обращаясь к рисунку, заметим, что поскольку силовые линии электрического вектора здесь параллельны поперечной координате , во внутреннем пространстве волновода можно установить две идеально проводяшие перегородки. отстоящие друг от друга на расстояние . В силу перпендикулярности векторов поля Е к этим перегородкам граничные условия на последних будут выполняться автоматически. Таким образом, можно рассматривать лишь поля, существующие в замкнутой области с прямоугольной формой сечения, то есть перейти к прямоугольному волноводу.

Чрезвычайно важно отметить, что данная картина поля останется справедливой при любом расстоянии между перегородками или, согласно принятой здесь терминологии, при любом размере узкой стенки волновода. Отсюда следует, что величина не должна входить в выражение, определяющее критическую длину волны для данного типа колебаний. Действительно, при , будем иметь

.

Поскольку волна типа в рассматриваемом волноводе является низшим типом колебаний, можно сформулировать полученный результат следующим образом: по прямоугольному волноводу могут передаваться лишь колебания с длинами волн, меньшими, чем удвоенный размер широкой стенки; более длинноволновые колебания по волноводу принципиально распространяться не могут.

Передачу электромагнитной энергии от генератора к нагрузке по волноводу следует вести на основном типе колебаний , так как анализ показывает, что при этом потери энергии в волноводе минимальны. Для того, чтобы в волноводе имели место только колебания типа , необходимо выбрать рабочую длину волны менее , но более , , и других критических длин волн. Практически необходимо соблюдать условие

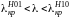
Для волны типа значения индексов и показывают, что в направлении оси распределению амплитуд составляющих напряженности поля соответствует одна полуволна, а в направлении оси поле однородно. Вся совокупность силовых линий движется вдоль оси с фазовой скоростью .

43. Критическая длина волны и длина волны в прямоугольном волноводе

На основании материала, рассмотренного выше, имеем

.

Напомним, что входящие в это уравнение постоянная распространения в свободном пространстве и продольное волновое число очень просто связаны с длиной волны генератора и длиной волны в волноводе :

, .

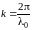В свою очередь, поперечное волновое число , определяемое формулой , зависит лишь от геометрических размеров сечения и от индексов выбранного типа волны и совершенно не зависит от частоты.

Выражение для поперечного волнового числа позволяет вскрыть важнейшую особенность работы любого волновода рассматриваемого типа. Если , то продольное волновое число является вещественным, а это, как уже известно, означает распространение данного колебания в виде бегущих волн. Ести длина волны генератора увеличена настолько, что , то вместо бегущей волны в волноводе существуют нераспространяющиеся колебания, амплитуда которых экспоненциально уменьшается по координате . Об этом свидетельствует мнимый характер продольного волнового числа .

Граничный случай возникает, когда равно . При этом и, как следствие, . Принято говорить, что в данных условиях рассматриваемый тип колебаний находится в критическом режиме. Значение длины волны генератора, соответствующее случаю , называется критической длиной волны для данного типа колебаний в исследуемом волноводе и обозначается . Из приведенных рассуждений следует, что 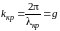, откуда

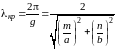
Вся область длин волн, меньших, чем , является областью «прозрачности» данного волновода на рассматриваемом типе колебаний; причем, если , то длина волны в волноводе лишь в очень малой степени отличается от длины волны в свободном пространстве, всегда превосходя ее. Всю область частот, которой соответствуют , называют областью непрозрачности или областью отсечки.