40. Волны типа е в прямоугольном волноводе

Как уже упоминалось, волны Е-типа (или типа ТМ) в линиях передачи характеризуются тем, что в их электромагнитных полях присутствуют продольные составляющие электрического поля, тогда как магнитное поле таких волн поперечно. Другими словами, , .

Этот характер составляющей позволяет однозначно выразить все поперечные составляющие электромагнитного поля любой волны типа Е через частные производные от продольной составляющей по поперечным координатам.

Таким образом, если удается найти составляющую поля в каждой точке внутренней области волновода, то задача будет решена полностью.

В прямоугольном волноводе возможно существование сколь угодно большого числа волн типа Е. Однако из сказанного следует, что волн типа и не существует.

Картина мгновенного распространения силовых линий векторов и для простейшей волны типа .

Картина мгновенного распределения линий электромагнитного поля волны типа

Данная картина поля, в которой по обеим поперечным осям укладывается по одной стоячей полуволне, позволяет построить картину поля для любого более сложного колебания типа Е. При этом изображенное здесь распределение следует «повторить» такое число раз, котое равно значению индекса требуемого типа волны по той или иной координатной оси. Поскольку зависимости составляющих полей описываются гармоническими функциями координат, направление стрелок на силовых линиях в соседних пучностях стоячих волн должно чередоваться. Пример такого построения для волны типа приведен на рисунке .

Картина распределения линий поля волны типа

41. Волны типа н в прямоугольном волноводе

Волны типа Н характеризуются тем, что здесь магнитное поле имеет продольную составляющую , в то время как электрическое поле поперечно, т.е. .

Будем предполагать, что геометрия и физические параметры волновода остаются такими же, как при рассмотрении волн типа Е. Все составляющие электромагнитного поля могут быть выражены через составляющую с помощью формул перехода.

Выясним вопрос о том, какой тип волны в прямоугольном волноводе является низшим, т. е. обладает наибольшей критической длиной волны. Из анализа формулы критической длины волны следует, что наибольшей критической длиной волны будет характеризоваться тот тип колебаний, которому соответствуют наименьшие индексы. Поскольку для волн Н-типов в данном случае один из индексов, но не оба вместе, может равняться нулю, так как при и все составляющие напряженностей поля равны нулю. В то же время известно, что для волн Е-типа такая ситуация невозможна. Это значит, что низший тип колебаний в прямоугольном волноводе принадлежит к классу волн Н-типа.

Наименьшими значениями и , при которых напряженность и отличаются от нуля, будут , и , , то есть волны типа и соответственно. Критические длины волн для этих типов волн в соответствии с общим выражением будут:

, .

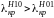При обсуждении постановки задачи условились считать, что размер сечения волновода по координате больше, чем по координате , т. е. . Отсюда следует, что , то есть из двух колебаний с наименьшими из возможных индексов, наибольшей критической длиной волны будет обладать тип колебаний .