33. Падение плоской электромагнитной волны на диэлектрическое полупространство под произвольным углом. Законы Снеллиуса.

Рассмотрим наиболее общий случай, при котором плоская электромагнитная волна, распространяясь в среде 1, падает на границу раздела под произвольным углом , удовлетворяющим условию . Геометрия данной задачи и направление осей координат показаны на рисунке.

При анализе этой системы естественно выделить три волны: падающую, отраженную и преломленную. Векторы Пойнтинга всех трех перечисленных волн лежат в одной плоскости, названной плоскостью падения.

Из рисунка следует, что вектор образует с положительными направлениями осей , , углы , и соответственно.

На границе раздела, т.е., в плоскости , должны выполняться условия непрерывности тангенциальных составляющих векторов и , т.е.

, при .

Таким образом, получены два хорошо известных из элементарной физики закона, определяющих поведение волн на границе раздела двух сред. Эти законы носят название законов Снеллиуса (Снелля) и формулируются следующим образом:

1. Угол падения равен углу отражения.

2. Отношение синусов угла падения и преломления равно обратному отношению показателей преломления.

Для каждой среды введем величину , носящую название показателя преломления данной среды. Если, например, , то принято говорить, что вторая среда обладает большей оптической плотностью, чем первая. Используется также понятие относительного показателя преломления двух сред . В этом случае закон Снеллиуса примет вид

.

34. Угол Брюстера

При падении плоских электромагнитных волн на границу раздела двух сред при определенных условиях коэффициент отражения может обратиться в нуль. Угол падения, при котором падающая волна полностью, без отражения, проникает из одной среды в другую, называется углом Брюстера или углом полного преломления и обозначается как .

Отраженная волна не может возникнуть, если оси упорядоченно ориентированных молекулярных диполей будут параллельны направлению, в котором должна распространяться отраженная волна.

Явление полного преломления можно наблюдать либо при перпендикулярной, либо при параллельной поляризации.

Угол Брюстера при падении плоской электромагнитной волны на немагнитный диэлектрик может существовать только при параллельной поляризации.

35. Угол полного внутреннего отражения

Обратимся вновь к формулировке второго закона Снеллиуса:

.

Здесь могут существовать два случая.

• Оптическая плотность среды 2 превосходит оптическую плотность среды 1, т.е. . При этом условии всегда , а поскольку угол падения лежит в интервале , то преломленная волна существует при любом угле падения.

• Среда 2 является оптически менее плотной, т.е. . Здесь всегда , поэтому найдется такое значение угла падения, при котором преломленная волна пойдет параллельно границе раздела под углом 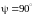. Данное критическое значение угла падения носит название угла полного внутреннего отражения:

.

При углах падения, больших угла полного внутреннего отражения преломленной волны в полном понимании не существует, энергия падающей волны полностью отражается внутрь первой среды.

Явление полного внутреннего отражения широко используется в оптике при построении волоконно-оптических линий (световодов).