Граничные условия для тангенциальных компонент векторов н и в
Задача о поведении на границе раздела тангенциальных составляющих магнитного поля решается на основе второго уравнения Максвелла (закон полного тока) в интегральной формулировке:
Проведем
через граничную поверхность
плоскость
,
проходящую через нормаль к
.
Введем в исследуемой точке
три взаимно ортогональных вектора
,
и
.
Векторы
,
по прежнему являются единичными векторами
нормального и тангенциального направлений
и лежат в плоскости
,
а
образует с ней нормаль.
Выделим
в окрестности точки
малый прямоугольный контур, целиком
лежащий в плоскости
таким образом, что две его стороны
пересекают границу раздела, а две лежат
по разные стороны от границы раздела.
Обозначим длину сторон контура
и
.
Зададим направление обхода контура по
направлению орта
(против часовой стрелки, наблюдая с
конца орта
).
Далее снова нужно рассмотреть два случая.
Первый случай. Электродинамические параметры обеих граничащих сред являются величинами конечными, т.е., не равными бесконечности. Отсюда непосредственно следует конечное значение векторов плотности токов проводимости и смещения.
Теперь совершим предельный переход, устремляя высоту контура к нулю. В силу предположения о конечности векторов тока проводимости и смещения будем иметь
.
Кроме
того, циркуляция вектора
по боковым сторонам контура также будет
равна нулю
.
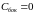С учетом сказанного будем иметь:
,
или
.
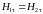Таким образом, при конечных значениях электродинамических параметров сред тангенциальные составляющие векторов напряженности магнитного поля непрерывны. Отсюда сразу следует, что тангенциальные составляющие векторов магнитной индукции терпят разрыв:
.
Рассмотрим теперь второй случай, считая, что проводимость одной из граничащих сред бесконечна.
Положим,
например, что бесконечна проводимость
второй среды
.
Подобное предположение делает неприменимой
формулу
.
Дело в том, то при бесконечно большой
проводимости среды толщина скин-слоя
(глубина проникновения электромагнитных
волн) равна нулю на любой частоте. В
результате токи проводимости протекают
по поверхностной пленке нулевой толщины,
и предельный переход даст отличный от
нуля результат.
Для
этого случая вводят понятие вектора
плотности поверхностного тока
.
Принцип введения этого вектора показан
на рисунке:
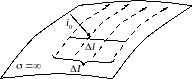
− Поверхностный ток
Прежде
всего проведем единичный вектор,
касательный к линиям тока в данной
точке. Этот вектор обозначается как
.
Затем находится величина тока
,
протекающего через отрезок
,
перпендикулярный вектору
.
Плотность поверхностного тока определяется
как
.
Теперь закон полного тока для контура можно записать в виде
.
Далее
следует учесть, что внутри идеального
проводника все составляющие
электромагнитного поля должны равняться
нулю. Так как бесконечно проводящей
принята вторая среда, то поэтому
и получим
.
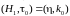Это выражение является граничным условием для тангенциальной составляющей вектора напряженности магнитного поля на границе с идеальным металлом. Данная формула позволяет решить важную для практики задачу − найти плотность поверхностного тока по известному магнитному полю на границе идеального проводника. С учетом того, что
,
можно записать
.
Таким
образом, поверхностный ток на границе
раздела с идеальным металлом протекает
в направлении, перпендикулярном вектору
,
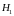и численно равен напряженности магнитного
поля.
Таким образом, на поверхности раздела любых двух изотропных сред должны выполняться следующие граничные условия:
.