40. Общие индексы как средние из индивидуальных индексов

Для определения агрегатных индексов необходимо иметь абсолютные значения индексируе-

мой величины и величины, с помощью которой достигается сравнимость уровней явлений, отдельные элементы которых непосредственно не подытоживаются, т.е. весов индексов и их соиз-

мерителей. Вместе с тем не всегда такие показатели имеются в отчетности, что не позволяет полу-

чить некоторые условные показатели необходимые для расчета общих индексов в агрегатной

форме, например, сумму товарооборота ∑q1p0. При невозможности найти ∑q1p0 общие индексы

рассчитывают в виде средних из индивидуальных.

Средние из индивидуальных индексов являются производными индексами, их получают

вследствие преобразования агрегатных индексов. Поэтому средний из индивидуальных индексов

тождественен агрегатному индексу.

Каждый агрегатный индекс может быть преобразован в средний индекс: средний арифмети-

ческий или средний гармонический.

Средний арифметический индекс целесообразно использовать тогда, когда в агрегатном ин-

дексе реальная величина (товарооборот - ∑p1q1 или ∑p0q0) находится в знаменателе дроби, а сред-

ний гармонический индекс целесообразно использовать тогда, когда в агрегатном индексе реаль-

ная величина находится в числителе дроби.

Так как в агрегатной форме общего индекса физического объема товарооборота знаменатель

формулы 10.3 является величиной реальной, а числитель – условною, то общий индекс физическо-

го объема товарооборота будет представлен в виде средней арифметической величины из индиви-

дуальных индексов физического объема товаров (iq), которые взвешены по стоимости продукции

базисного периода в базисных ценах (p0q0).

Общий индекс физического объема как средний из индивидуальных индексов рассчи-

тывается по формуле В агрегатной форме индекса цен числитель формулы 10.4 является величиной реальной, а

знаменатель – условною, поэтому общий индекс цен – это средняя гармоническая величина инди-

видуальных индексов цен (iр), взвешенных на сумму фактического товарооборота отчетного пери-

ода (p1q1).

Общий индекс цен как средний из индивидуальных индексов рассчитывается по формуле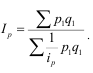

39. Агрегатный индекс как основная форма общего индекса

Агрегатные индексы являются основной формой экономических индексов.

При моделировании агрегатных индексов необходимо придерживаться общепринятого в ста-

тистике порядка символического обозначения соответствующих явлений,

Основная сложность построения общих индексов состоит в преодолении несоизмеримости

разных элементов, составляющих совокупность. Одним из возможных способов достижения этого

является введение в индекс дополнительного и при этом неизменного показателя, который эконо-

мически тесно связан с индексируемой величиной, называемого, как отмечалось в п. 10.1, соизме-рителем. Например, для количества продукции таким соизмерителем может быть как цена, так и

себестоимость или трудоемкость единицы продукции. Умножив объем каждого вида продукции

на соответствующий ему соизмеритель получают показатели, которые можно не только подыто-

жить, но и сопоставить полученные суммы между собой.

Механизм построения общих индексов рассмотрим на примере показателей физического

объема реализации отдельных видов продукции (q), их цен (p) и товарооборота (qp).

Сумма произведений количества продукции на его соизмериталь (цену) приводит к образо-

ванию объединений или агрегатов ∑qp («aggrego» – в переводе с латинского – присоединяю). По-

строенный на их основе общий индекс, в числителе и в знаменателе которого суммы произведе-

ний уровней признаков, получил название агрегатного индекса. Эта форма индекса более 100 лет

назад была разработана немецкими статистиками Э. Леспейресом (1874 г.) и Г. Пааше (1864 г.).

Перемножение агрегируемых признаков, позволяет не только решить проблему сопостави-

мости, а и учесть веса соизмерителей в реальных экономических процессах. Так, если индексиру-

емой величиной является качественный признак, то в общем индексе его уровень умножается на

значения связанного с ним количественного показателя, который играет роль веса.

Для определения изменения стоимости реализованной продукции в текущем периоде по

сравнению с базисным используется общий индекс, называемый в статистике индексом товаро-

оборота (Ipq), рассчитываемый по формуле Приведенный индекс характеризует изменение сложного явления - товарооборота под влия-

нием таких факторов: изменения физического объема продажи отдельных товаров и изменения

цен, по которым они реализовывались. Чтобы изучить влияние одного из этих факторов на изме-

нение товарооборота, следует другой принять условно неизменным, т.е. зафиксировать его на

уровне определенного периода.

В отечественной статистической практике принят следующий порядок фиксирования созме-

рителей (весов):

- при построении индексов качественного признака его веса фиксируются на уровне отчет-

ного периода;

- при построении индексов количественных (объемных) признаков – признаки-соизмерители

фиксируются на уровне базисного периода.

Этот принцип обеспечивает возможность построения системы взаимозависимых индексов.

Как изменился товарооборот только за счет изменения количества проданных товаров в от-

четном периоде по сравнению с базисным периодом, позволяет оценить общий индекс физиче-

ского объема товарооборота (Iq), рассчитываемый по формуле