6. Теплообмен при вынужденном движении жидкости

Движение жидкости в трубах может быть ламинарным и турбулентным в зависимости от числа Рейнольдса. Ламинарное движение наблюдается при Значение является нижним критическим значением числа Рейнольдса. При возмущения потока необратимо нарушают ламинарный режим движения и способствуют турбулизации потока. Однако турбулентное движение устанавливается при При числах Рейнольдса от до движение жидкости является переходным от ламинарного к турбулентному.

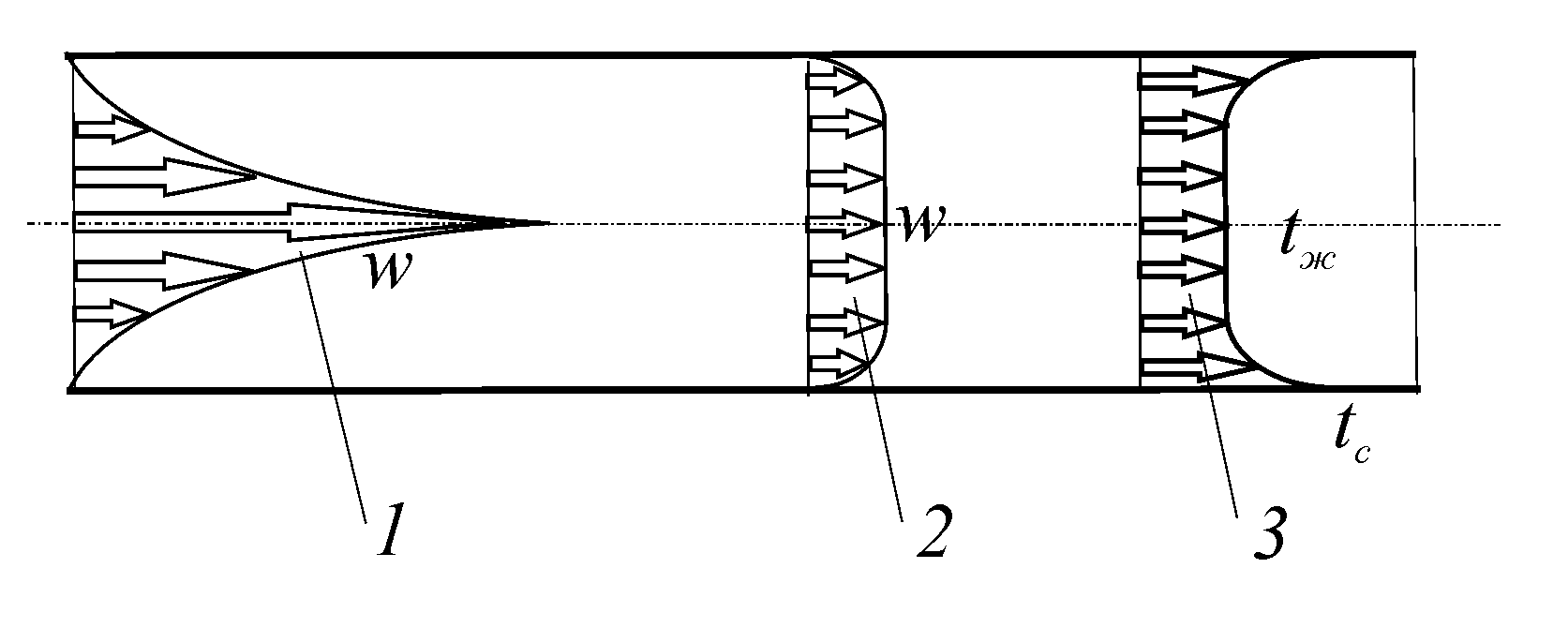
Рис. 10. Развитие течения при вынужденном движении в трубе

На рис. 10 показана длина гидродинамического начального участка (1) в котором пограничный слой достигает оси трубы. Длина участка гидродинамического стабилизации увеличивается с ростом числа Re и уменьшается с усилением возмущения потока на входе в трубу.

При турбулентном движении распределение скорости имеет вид усеченной параболы (рис. 10) - 2 форма, которой зависит от величины числа Re. С увеличением числа Рейнольдса наблюдается резкое изменение скорости вблизи стенки и пологое ее изменение в центральной части трубы.

Теплообмен в трубе существенно зависит от гидродинамической картины движения жидкости. В теплообмене участвует только пристенный пограничный слой, а остальная часть сечения, составляющая ядро потока, с температурой, равной температуре на оси, в теплообмене не участвует. До тех пор, пока тепловой пограничный слой не достигнет оси трубы, температура жидкости на оси трубы остается равной ее значению во входном сечении (рис. 10) - 3. Изменение температуры на оси трубы вниз по потоку начинается с сечения, где тепловой пограничный слой достигает оси.

Длина участка тепловой стабилизации зависит от большого числа различных факторов, из которых главными факторами являются: число Рейнольдса, физические свойства жидкости, условия входа в трубу.

Теплообмен при ламинарном движении жидкости в трубах

При ламинарном течении жидкости в трубах возможны два режима движения: вязкостный и вязкостно-гравитационный.

При вязкостном режиме движения силы вязкости преобладают над подъемными силами в жидкости. Такой режим наблюдается при ламинарном движении жидкостей с большой вязкостью в трубах малого диаметра и при малых температурных напорах.

При вязкостно-гравитационном режиме движения жидкостей подъемные силы велики и заметное влияние на перенос теплоты оказывает свободная конвекция. На распределение скорости по сечению трубы в сильной мере влияет изменение вязкости, а также интенсивность и направление свободного движения.

Вязкостный режим существует при (GrPr) < 8·10⁵ , средний коэффициент теплоотдачи при этом режиме определяется из уравнения

(128)

Формула действительна при , t_с=const. и

Определяющим линейным размером является внутренний диаметр трубы; определяющей температурой принята температура (знак минус при нагревании и плюс при охлаждении); – средний логарифмический температурный напор.

Вязкостно-гравитационный режим существует при (GrPr) >8·10⁵, средний коэффициент теплоотдачи в этом случае определяется по формуле

(129)

Формула (129) действительна при 1/d > 50; за определяющий линейный размер принят внутренний диаметр трубы; за определяющую температуру – средняя температура потока.

Теплообмен при турбулентном движении жидкости в трубах

Для определения среднего коэффициента теплоотдачи при развитом турбулентном движении обычно используется формула М. А. Михеева

(130)

В качестве определяющего линейного размера здесь принят внутренний диаметр трубы; определяющая температура – средняя температура потока; формула (130) действительна при l/d >50. Если течение жидкости происходит по каналам некруглого сечения, то в качестве определяющего линейного размера принимается эквивалентный диаметр, определяемый по формуле d_э=4f/u, где f – площадь поперечного сечения канала (живое сечение); u – полный смоченный периметр канала.

Более интенсивно, чем в прямых трубах, протекает процесс теплоотдачи в изогнутых трубах (змеевиках). Для вычисления коэффициента теплоотдачи при турбулентном движении в змеевике можно использовать соотношение гдe α_зм – коэффициент теплоотдачи в изогнутой трубе; α – коэффициент теплоотдачи в прямой трубе, вычисленный по формуле (130); d – диаметр трубы; R – радиус змеевика

Теплообмен при поперечном обтекании труб жидкостью

Одиночные трубы. Теплообмен при поперечном обтекании жидкостью трубы (рис. 11.) зависит от гидродинамической картины жидкости около поверхности. Обтекание трубы может быть плавным – безотрывным и отрывным. Плавное безотрывное обтекание трубы наблюдается только при .

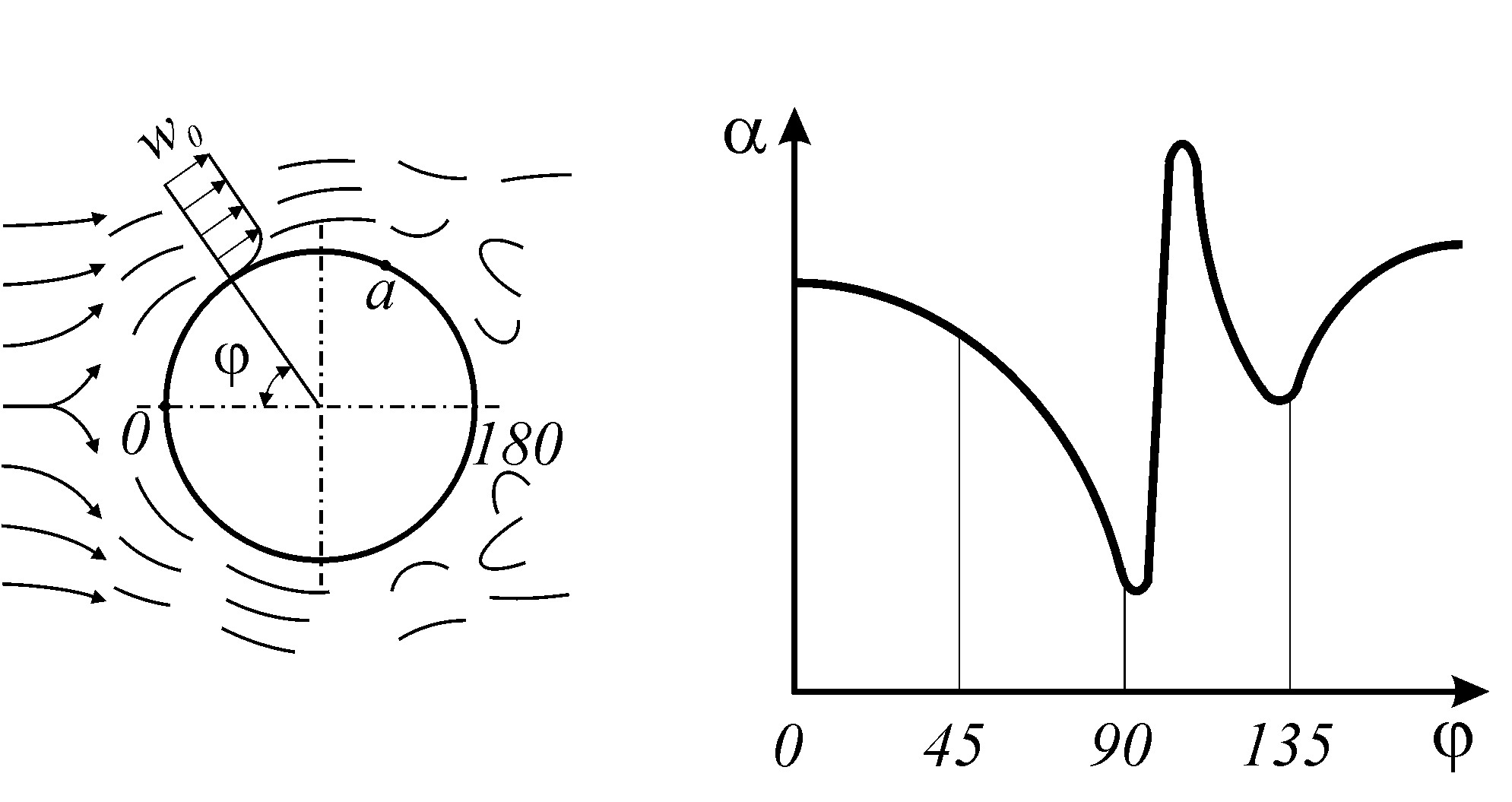
Рис. 11. Схема движения и график изменения коэффициента

теплоотдачи при поперечном обтекании трубы

При Re>5 пограничный слой, образующийся на передней половине трубы, в кормовой части отрывается от поверхности; позади трубы образуются два симметричных вихря.

В соответствии с этим меняется коэффициент теплоотдачи по поверхности трубы. В лобовой части он наибольший, далее по периметру трубы коэффициент теплоотдачи α падает и достигает минимального значения в точке отрыва потока (точка а). В вихревой части коэффициент теплоотдачи увеличивается.

Для определения коэффициента теплоотдачи при поперечном обтекании одиночной трубы используют следующие уравнения подобия:

при Re = 5 – 10³

(131)

при Re = 10³ – 2·10⁵

(132)

За определяющий линейный размер принят внешний диаметр трубы; за определяющую температуру – температура набегающего потока; скорость жидкости отнесена к самому узкому сечению канала, в котором расположена труба.

Формулы (131 и 132) справедливы при условии, что угол между направлением потока и осью трубы, называемой углом атаки, равен 90º. При уменьшении угла атаки уменьшается. Если угол атаки меньше 90º, то полученный коэффициент теплоотдачи необходимо умножить на поправочный коэффициент , приближенные значения множителя можно определить по формуле

. (133)

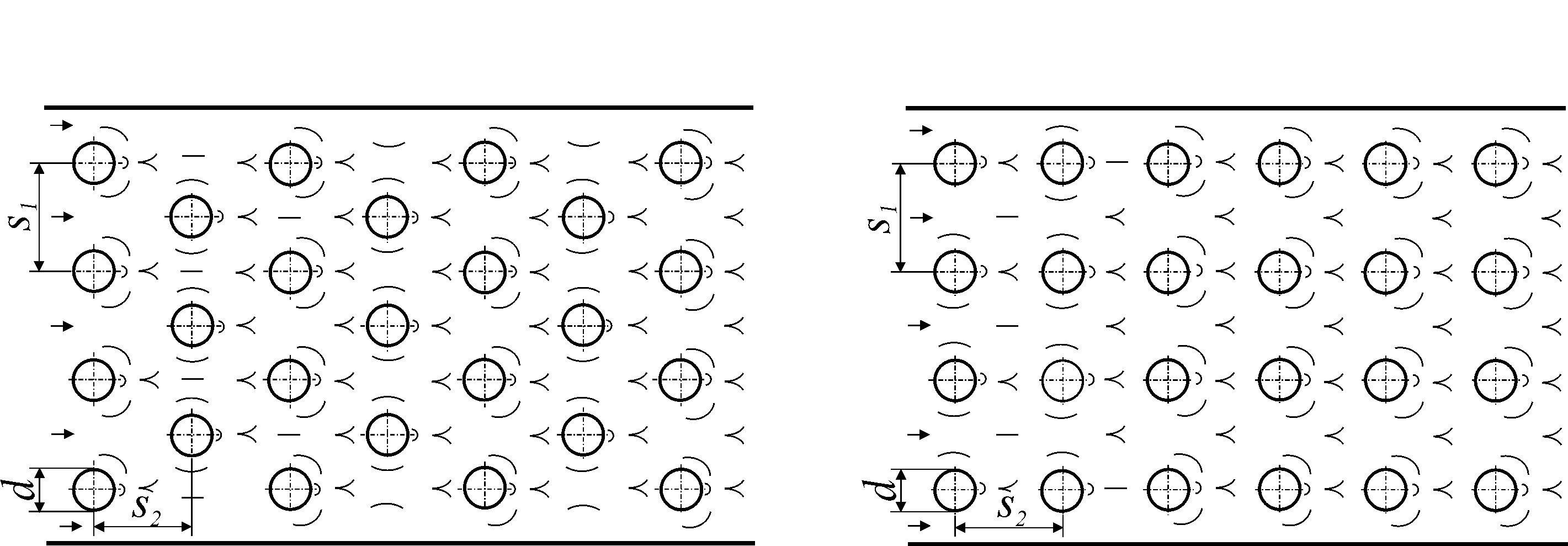
Пучки труб. При поперечном обтекании потоком жидкости пучка труб интенсивность теплоотдачи зависит не только от факторов, влияющих на теплоотдачу одиночной трубы, но и от взаимного расположения труб в пучке, а также от плотности пучка. Обычно применяют коридорное (по вершинам квадрата) и шахматное (по вершинам треугольника) расположение труб в пучке (рис. 12).

а б

Рис. 12. Схемы расположения труб в пучках: (а) – шахматное; (б) – коридорное расположение ( – поперечный и продольный соответственно шаги труб)

Плотность расположения труб в пучке характеризуется соотношениями между поперечным шагом S₁, продольным шагом S₂ и внешним диаметром труб d.

Исследованиями установлено, что теплоотдача труб второго и третьего рядов постепенно возрастает по сравнению с теплоотдачей первого ряда. Это объясняется увеличением турбулентности потока при прохождении его через пучок труб. Начиная с третьего ряда поток практически стабилизируется, поэтому и средний коэффициент теплоотдачи для всех последующих рядов сохраняет постоянное значение. Если значение коэффициента теплоотдачи третьего ряда (и последующих рядов) α₃, то в коридорном пучке для первого и второго ряда труб коэффициент теплоотдачи α₁=0,6 α₃ и α₂ =0,9 α₃, при

шахматном расположении α₁=0,6 α₃ и α₂ =0,7 α₃. Средний коэффициент теплоотдачи для третьего и последующих рядов определяется из уравнения подобия

(134)

Для шахматных пучков С=0,41; n=0,6; для коридорных пучков С=0,26, n=0,65. Поправочный коэффициент ε_S учитывает влияние относительных

шагов; для шахматного пучка при < 2, ε_S =( )^1/6; при ≥2, ε_S=1,12; для коридорного пучка ε_S =( )^-0,15. Формула (134) действительна при Re =10³– 10⁵. В качестве определяющего линейного размера принят внешний диаметр труб; в качестве определяющей температуры – средняя

температура жидкости; скорость определяется в самом узком сечении пучка труб.

Среднее значение коэффициента теплоотдачи для всего пучка, состоящего из n рядов, определяется по формуле:

(135)

где F₁ , F₂,…, F_n – поверхности теплообмена в соответствующем ряду.

Если предположить, что в ряду F₁ = F₂= F₃,…, F_n и учитывая, что α₃=α₄= …=α_n, то можно написать

(136)

Принимая во внимание приближенные значения α₁ и α₂, получим:

для коридорного пучка

; (137)

для шахматного пучка

(138)

Теплообмен при продольном обтекании жидкостью

плоской поверхности

При обтекании плоской поверхности жидкостью около поверхности стенки образуются два пограничных слоя: гидродинамический и тепловой. В динамическом слое скорость жидкости изменяется от нуля на стенке до w₁ на внешней его границе. В тепловом пограничном слое температура изменяется от температуры на стенке до температуры внешнего потока. На рис. 13 показана схема движения жидкости вдоль плоской поверхности.

Движение в пограничном слое может быть ламинарным и турбулентным. Образующийся в начале обтекаемой поверхности ламинарный пограничный слой при достижении критического значения числа Рейнольдса может перейти в турбулентный слой с тонким ламинарным подслоем (пристенная область, где силы вязкости велики). Переход ламинарного движения в турбулентное происходит не в точке, а на некотором участке, в пределах которого движение жидкости является переходным.

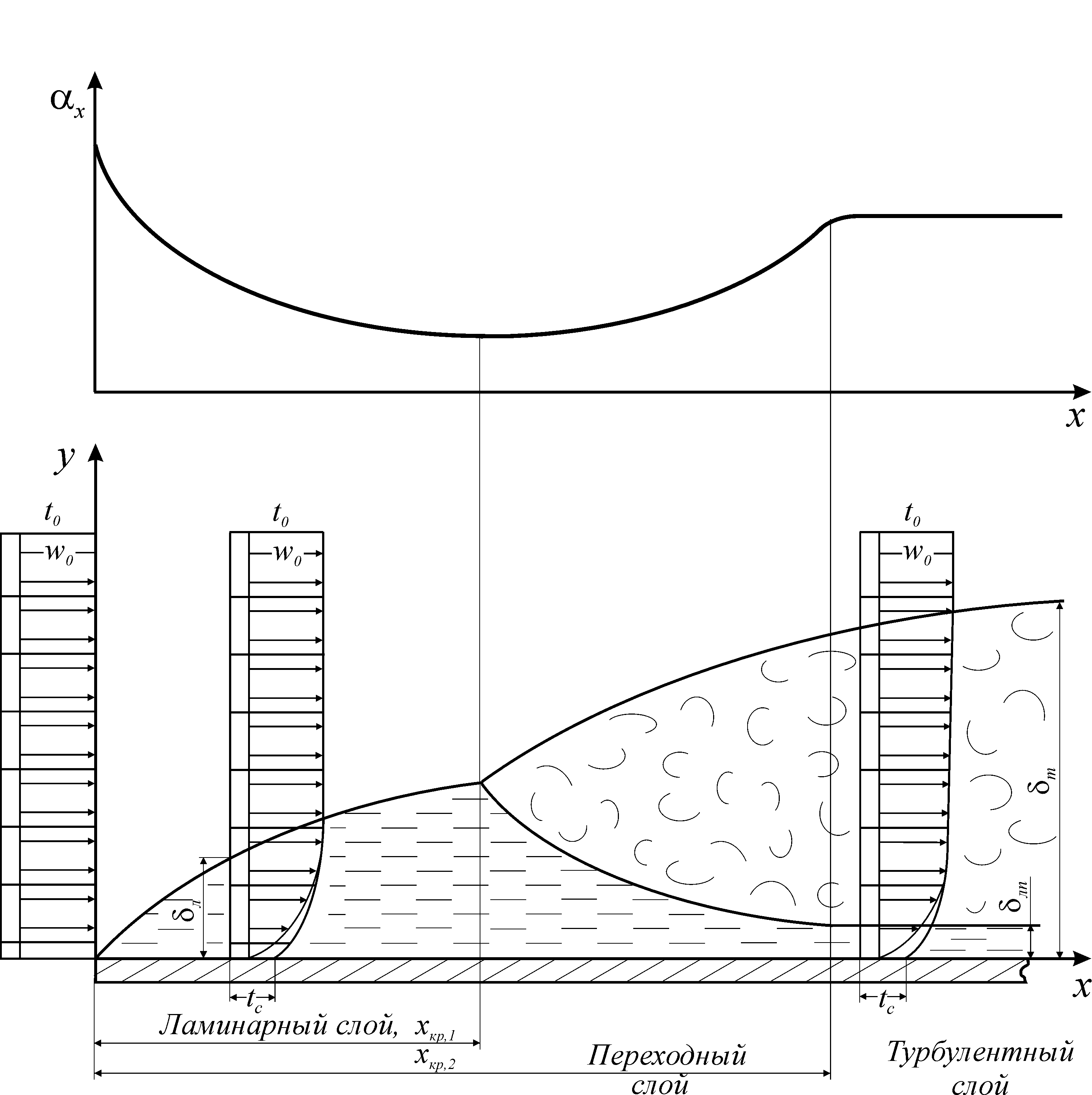
Рис. 13. Схема движения жидкости вдоль плоской поверхности

Среднее значение коэффициента теплоотдачи при обтекании плоской стенки определяется из уравнения

При ламинарном течении Rе ≤ 4·10⁴

, (139

При турбулентном течении Rе > 4·10⁴

. (140)

В этих формулах в качестве определяющей температуры принята температура жидкости вдали от тела (t₀=const.); в качестве определяющего линейного размера – длина пластины по направлению потока.