4. Основные положения конвективного теплообмена

Под конвективным теплообменом понимают форму передачи теплоты при движении жидкости или газа под влиянием двух процессов – конвекции и теплопроводности.

Конвекцией называется перенос макрочастиц жидкости в пространстве. Если эти частицы жидкости перемешаются из области с одной температурой в область с другой температурой, их перемещение сопровождается переносом теплоты. Перенос теплоты конвекцией сопровождается теплопроводностью при непосредственном соприкосновении различно нагретых частиц жидкости.

Количество теплоты, отдаваемое жидкостью твердой стенке или воспринимаемое жидкостью от стенки в единицу времени, определяется уравнением Ньютона –Рихмана

, (96)

а плотность теплового потока следующим образом:

, (97)

где α – коэффициент, характеризующий условия теплообмена между жидкостью и поверхностью твердого тела, называемый коэффициентом теплоотдачи, Вт/(м²·°C); – температурный напор, K.

В соответствии с формулой (97) по своему физическому смыслу коэффициент теплоотдачи есть плотность теплового потока (q) на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды. Коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре, равном единице.

Коэффициент теплоотдачи зависит от многих факторов. В наиболее общем случае является функцией формы и размера тела, режима движения жидкости, физических свойств жидкости, положения в пространстве и состояния поверхности теплообмена и других величин. Процесс теплоотдачи в зависимости от природы движения жидкости протекает различно.

Различают вынужденную и естественную конвекцию. В первом случае жидкость или газ движется за счет внешних для данного процесса сил (насос, вентилятор, ветер), во втором случае – за счет разности плотностей нагретых и холодных частиц жидкости. Возникновение и интенсивность свободного или естественного движения всецело определяется тепловыми условиями процесса и, зависят от рода жидкости, разности температур и объема пространства, в котором протекает процесс.

Свободное движение может появиться в жидкости (газе) с переменной плотностью, очевидно, только в том случае, когда жидкость находится в поле земного притяжения.

Вынужденное движение в общем случае может, сопровождается свободным движением. При больших скоростях вынужденного движения, влияние свободной конвекции становится пренебрежимо малым.

Основное уравнение теплоотдачи (96) имеет простой вид. Трудности возникают при определении коэффициента теплоотдачи. Практически изучение процесса теплоотдачи сводится к определению зависимости ( ) от различных факторов.

В дальнейшем будут рассмотрены только стационарные процессы течения и теплоотдачи. Условием стационарности является неизменность во времени скорости и температуры в любой точке жидкости.

Дифференциальные уравнения конвективного теплообмена

Дифференциальное уравнение теплообмена получается при рассмотрении передачи теплоты теплопроводностью через, практический, неподвижный слой жидкости (пограничный слой), который имеет место вблизи твердого тела, омываемого жидкостью ( ) и передачи теплоты к пограничному слою за счет конвективного теплообмена ( )

(98)

Дифференциальное уравнение энергии при условии однородности и несжимаемости жидкости, отсутствия внутренних источников теплоты и работы расширения, а также постоянства физических параметров жидкости в пределах элементарного объема формулируется следующим образом:

, (99

где - субстациальная (полная) производная;

- характеризует локальное изменение температуры во времени в какой-либо точке жидкости; – характеризует конвективное изменение температуры при переходе от точки к точке.

При уравнение (99) переходит в уравнение теплопроводности для твердого тела без внутренних источников теплоты.

Дифференциальное уравнение неразрывности получается на основе закона сохранения массы и, для сжимаемой жидкости имеет следующий вид:

. (100)

В частном случае несжимаемых жидкостей . уравнение (100) запишется в виде

. (101)

Уравнение движения (уравнение Навье-Стокса) получается на базе первого и второго законов Ньютона и в векторной форме записи можно представить в виде

(102)

где - плотность; - полная производная; p – давление; g – ускорение свободного падения; - динамический коэффициент вязкости.

Полученная система дифференциальных уравнений описывает бесчисленное множество конкретных процессов.

Точные решения этой системы имеются только для отдельных частных случаев при ряде упрощающих предпосылок.

Основы теории подобия и метода анализа размерностей

В связи с ограниченными возможностями аналитического решения

дифференциальных уравнений конвективного теплообмена решающее зна-

чение приобретает эксперимент.

Цель экспериментального исследования получение на основе экспериментальных данных уравнений, по которым можно затем вести расчет теплообмена в подобных процессах.

Для этого необходимо сформулировать основные условия, при выполнении которых процессы будут подобны.

На все эти вопросы дает ответы теория подобия. Понятие подобия заимствовано из геометрии, где рассматриваются условия подобия геометрических фигур. Для подобия геометрических фигур достаточно соблюдения обычных признаков подобия (пропорциональность сходственных сторон, равенство углов и др.). Для подобия физических процессов необходимо говорить о подобии физических величин и явлений. Два или несколько явлений будут подобны, если подобны все физические величины , характеризующие эти явления, т.е. подобные между собою явления имеют одинаковые безразмерные комплексы - критерии подобия. Этот вывод свидетельствует о том, что в опытах нужно измерять те величины, которые входят в критерии подобия, характеризующие данный процесс.

Важной теоремой теории подобия является утверждение о том, что решение дифференциального уравнения, описывающего данный процесс, может быть представлено в виде функциональной зависимости между критериями подобия, характеризующими этот процесс и полученными из исходного уравнения. Это утверждение говорит о том, опытные данные надо обработать в виде зависимости между критериями подобия.

Наряду с приведенными выше двумя теоремами подобия, важным является и утверждение о том, что подобны между собой те явления, которые принадлежат к одному классу, к одному роду и имеют равные определяющие критерии подобия. Этот вывод позволяет полученные в опыте расчетные зависимости распространить на группу явлений, подобных исследованному.

Таким образом, теория подобия, при наличии дифференциальных уравнений, описывающих рассматриваемый процесс, позволяет, не решая сами уравнения, получить выражения чисел (критериев) подобия и на их основе получить расчетные зависимости – уравнения подобия.

При отсутствии дифференциальных уравнений, описывающих изучаемый процесс, используется метод анализа размерностей. Однако в этом случае должен быть известен перечень основных величин, оказывающих существенное влияние на развитие рассматриваемого процесса.

Например, для свободной конвекции такой перечень величин определяется следующей исходной зависимостью:

(103)

где – характерный для данного процесса линейный размер, м; – коэффициент объемного расширения; ρ – плотность жидкости; μ – динамический коэффициент вязкости; λ – коэффициент теплопроводности жидкости; – разность температур стенки и жидкости, °C; с_p – удельная теплоемкость жидкости, Дж/(кг·K).

Непосредственное экспериментальное исследование этой зависимости вследствие необходимости проведения большего числа опытов неосуществимо.

Теория размерностей в этом случае позволяет свести данное выражение от семи независимых переменных к зависимости от двух обобщенных безразмерных переменных (к уравнению подобия).

Критерии подобия и критериальные уравнения

Рассмотрим безразмерные комплексы величин, входящие в дифференциальные уравнения, преобразованные в безразмерные уравнения:

(104)

где – кинематический коэффициент вязкости.

Записанные безразмерные комплексы, составленные из размерных величин, называются критериями подобия.

Критерий Нуссельта характеризует соотношение тепловых потоков, передаваемых конвекцией и теплопроводностью, является обычно искомой величиной, поскольку в него входит коэффициент теплоотдачи

. (105)

Критерий Рейнольдса характеризует соотношение между силами инерции и молекулярного трения (вязкости)

, (106)

где w – средняя (линейная) скорость жидкости (м/с).

Критерий Прандтля характеризует физические свойства жидкости и их влияние на конвективный теплообмен

, (107)

Критерий Пекле характеризует отношение плотности теплового потока, передаваемого конвекцией, к плотности теплового потока, передаваемого теплопроводностью

(108)

Критерий Грасгофа характеризует соотношение подъемной силы, возникшей вследствие разности плотностей нагретых и холодных частиц жидкости и силы молекулярного трения и является параметром интенсивности свободного движения жидкости

(109)

Характеристики теплофизических свойств жидкостей, входящие в выражение чисел подобия, в общем случае зависят от температуры. Поэтому для определения численных значений критериев подобия указывается температура, при которой берутся теплофизические характеристики.

Как было рассмотрено ранее, система дифференциальных уравнений, характеризующая процесс, приводится к безразмерному виду при соответствующих условиях однозначности. В конечном счете получается общий вид критериального уравнения

(110)

Важное значение, при решении задач нестационарной теплопроводности, имеют критерии подобия (Фурье) и (Био).

Выражение для критериев и получены путем анализа дифференциальных уравнений теплообмена и теплопроводности (92 и 93).

Критерий Фурье ( ) - характеризует безразмерное время.

Написание Критерия Био похоже на форму записи критерия Нуссельта

, (111)

где – коэффициент теплопроводности твердого тела (в то время как в критерий Нуссельта - относится к окружающей среде)

Уравнения вида (110) называется критериальными.

В случае теплообмена, осложненного массообменном и изменением агрегатного состояния жидкости в процессе теплообмена, критерий Нуссельта зависит еще от ряда критериев.

Следует отметить, что. поскольку критериальные уравнения получены на основе эксперимента, в каждом случае указывается диапазон применимости уравнения, что принимается в качестве определяющей температуры и

линейного размера при определении соответствующих критериев.

Обработка и обобщение результатов эксперимента

Предположим, что анализ конвективного теплообмена в условиях вынужденного движения , позволил установить, что коэффициент теплоотдачи, а следовательно, и критерий Нуссельта, зависит

(112)

Из эксперимента определяют необходимые величины, входящие в критерии подобия, и подсчитывают их значения. Предположим, что зависимость между критериями подобия имеет степенной вид т.е.

(113)

где c, n, m – безразмерные постоянные величины.

Логарифмируя (112) получаем

(114)

Наносим опытные значения критериев подобия во всем диапазоне проведенных исследований на график (рис. 7).

Очевидно, если связь (112) действительно является степенной, получим семейство прямых линий, каждая из которых соответствует определенному значению критерия

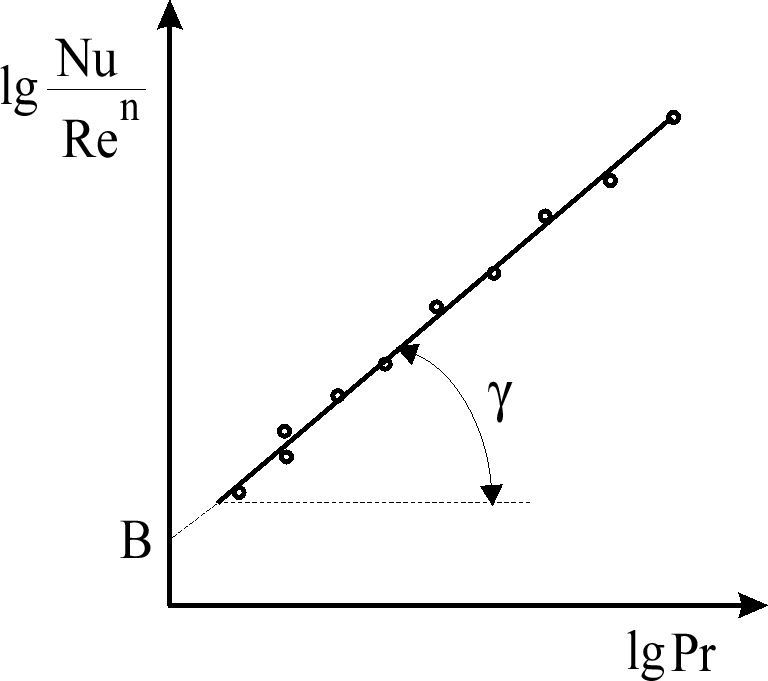
Рис. 7. Обобщение опытных данных в критериальной форме

В этом случае показатель степени при определится как

, (115)

где - угол наклона прямых линий к оси

Затем опытные данные наносят на график в координатах

(116)

Из этого графика определяют показатель степени m при критерии Pr

, (117)

где – угол наклона прямой к оси .

Постоянная с определяется из соотношения

(118)

Таким образом, определяются все постоянные коэффициенты в критериальных уравнениях.