2. Теплопроводность при стационарном температурном поле

Теплопроводность представляет собой процесс передачи теплоты путем непосредственного соприкосновения тел или отдельных частей тела, имеющих различную температуру. При этом процесс теплообмена происходит за счет передачи энергии микродвижения одних частиц другим.

В чистом виде теплопроводность наблюдается в твердых телах, а также в неподвижных газах и жидкостях в том случае, когда в них отсутствует конвекция.

В металлах перенос теплоты осуществляется путем движения (диффузии) свободных электронов; передача теплоты за счет упругих колебаний кристаллической решетки второстепенна. В жидкостях и твердых телах – диэлектриках теплопроводность осуществляется упругими волнам.

В газообразных телах распространение теплоты теплопроводностью происходит вследствие обмена энергией при соударении молекул, имеющих различную скорость теплового движения (путем диффузии молекул и атомов).

Стационарная теплопроводность

Необходимым условием распространения теплоты является неравно-

мерность распределения температуры в рассматриваемой среде. Таким образом, для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела.

Согласно закону Фурье количество теплоты проходящий через элемент изотермической поверхности за промежуток времени , пропорционально температурному градиенту

, (5)

где – коэффициент пропорциональности есть физический параметр вещества и называется коэффициентом теплопроводности, Вт/(м·°C); – элементарная площадь поверхности теплообмена, м²; – временной промежуток, сек.

Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности , называется плотностью теплового потока.

Количества теплоты , проходящее в единицу времени через изотермическую поверхность , называется тепловым потоком (Дж/с =Вт)

. (6)

Величина теплового потока и плотность теплового потока являются векторами, за положительное направление которых принимают направление по нормали к изотермической поверхности в сторону уменьшения температуры (рис.1).

Скалярная величина вектора плотности теплового потока будет равна:

. (7)

Скалярная величина вектора теплового потока будет равна:

. (8)

Знак минус в правой части уравнений (7 и 8) указывает на то, что тепловой поток и температурный градиент как векторы имеют противоположные направления.

Полное количество теплоты равно

. (9)

Выражение плотности тепловых потоков в направлении осей может быть записано в виде:

; ; . (10)

Вектор теплового потока с учетом (10) для трехмерной задачи составит

, (10а)

где – единичные векторы в направлении .

Коэффициент теплопроводности

Под коэффициентом теплопроводности понимают тепловой поток, передаваемый через единичную поверхность при единичном значении темпера-

турного градиента

. (11)

Для каждого тела коэффициент теплопроводности имеет свое численное значение и, зависит от природы, пористости, влажности, давления, температуры и других параметров. Численное значение определяется опытным путем. В практических расчетах используют значения коэффициента теплопроводности, которые приводятся в справочных таблицах. При выводе уравнения (7) принято, что не зависят от температуры и, является постоянной величиной. Однако, как показывают опыты, для многих материалов с достаточной для практики степенью точности, зависимость коэффициента теплопроводности от температуры можно принять линейной во всем рассматриваемом интервале температур

(12)

где – коэффициент теплопроводности при температуре ; b – постоянная, характеризующая приращение (уменьшение) материала при повышении его температуры на 1К.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и изменяется в пределах 0,005 – 0,5 Вт/(м·К).

Коэффициент теплопроводности жидкостей лежит в пределах 0,07 – 0,7 Вт/(м·К) и, как правило (за исключением воды и глицерина), уменьшается с увеличением температуры.

Наилучшими проводниками теплоты являются металлы, у которых Вт/(м·К). У большей части металлов с возрастанием температуры он уменьшается.

Дифференциальное уравнение теплопроводности

Распределение температуры в теле, описывается дифференциальным

уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:

, (13)

где – время, сек; – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, ;

– теплоемкость тела, ; – плотность тела, кг/м³; – объемная плотность тепловыделения, Bm/м³; – оператор Лапласа.

Уравнение (13) называется дифференциальным уравнением теплопроводности.

В цилиндрических координатах уравнение (13) имеет следующий вид:

, (14)

где – радиус вектор; – угол наклона радиуса–вектора.

Чтобы получить конкретное решение уравнения (13) для рассматриваемого случая, необходимо ввести полное математическое описание данного конкретного процесса теплопроводности. Эти частные особенности называются условиями однозначности или краевыми условиями, включающими:

• геометрические условия (форма, размеры тела);

• Физические условия (физические свойства тела и его физические параметры);

• Начальные условия (распределение температуры в теле в начальный момент времени);

• Граничные условия, определяющие взаимодействие тела с окружающей средой.

1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени

(15)

где -температура поверхности тела.

В частном случае, если температура поверхности тела постоянна выражение (15) имеет вид .

2. Граничные условия второго рода. Задается распределение плотности тепловогопотока на поверхности тела, как функция координат и времени

. (16)

В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем .

3. Граничные условия третьего рода. Задается температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой

если , (17)

Уравнение (17) выражает закон Ньютона-Рихмана. Теплота, воспринятая поверхностью тела, распространяется в нем по закону Фурье. Следовательно, где – коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1К, Вm/(м²К

на основании уравнений (16) и (17) имеем

. (18)

Индекс “с” означает, что температурный градиент относится к поверхности тела.

Выражение (18) можно записать в виде

. (19)

Уравнение (19) является аналитическим выражением граничных условий третьего рода.

4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные значения коэффициентов теплопроводности. Между телами предполагается идеальный контакт. Тогда

, (20)

где – коэффициент теплопроводности первого тела; – коэффициент те-плопроводности второго тела.

Теплопроводность плоской стенки

При установившемся (стационарном) тепловом режиме , поэтому уравнение (13) принимает вид

или . (21)

Развернутая форма оператора зависит от выбранной системы координат. При отсутствии внутренних источников теплоты , уравнение теплопроводности при стационарном температурном поле запишется в виде

. (21а)

Определим тепловой поток теплопроводностью через изотропную плоскую стенку, предполагая, что температура меняется только в направлении,

перпендикулярном плоскости стенки (рис.2а) имеем:

(22)

и

. (22а)

Интегрируя уравнение (22а) имеем

. (23)

Второе интегрирование дает

. (24)

а

б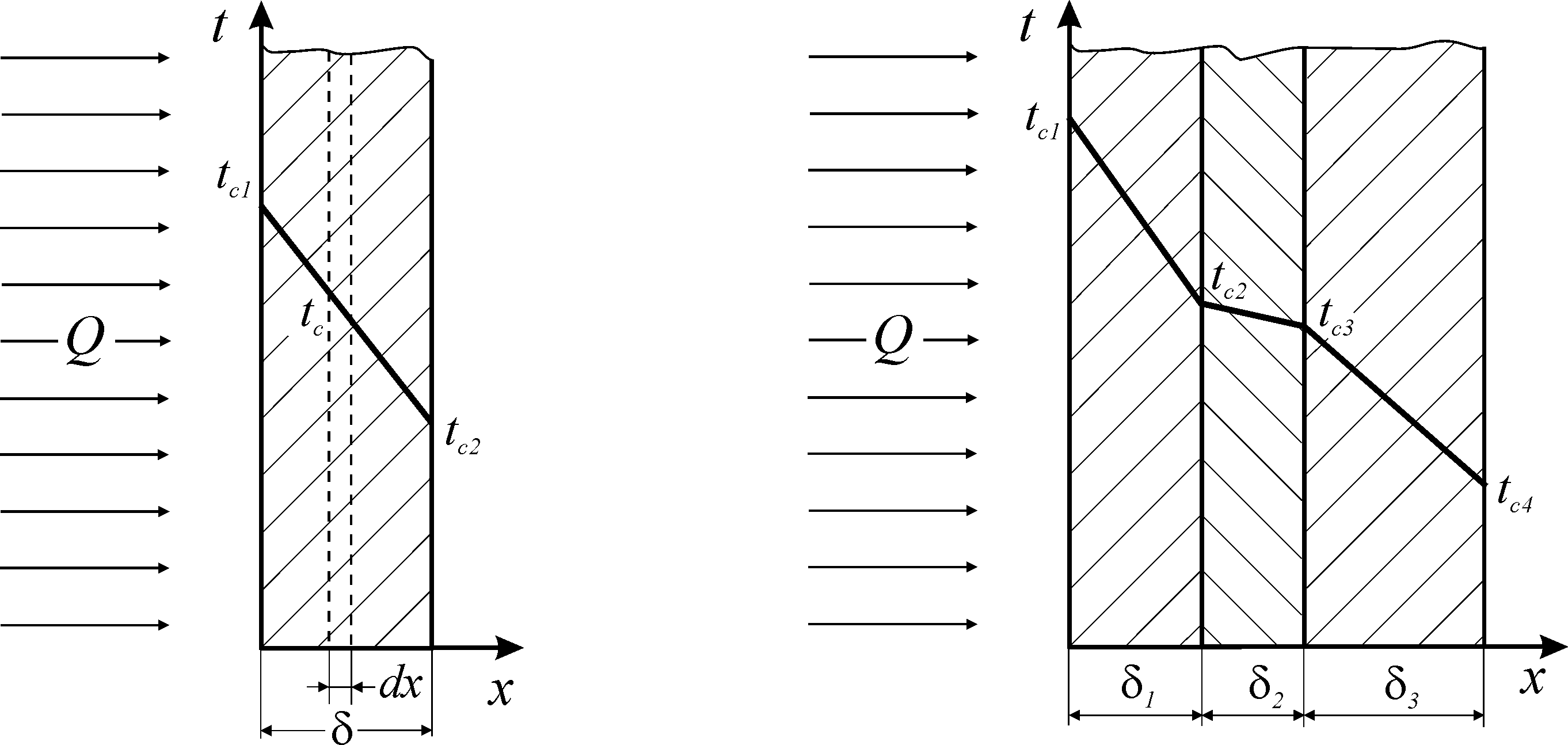

Рис. 2. Теплопроводность плоской однослойной (а) и многослойной

стенки (б)

Постоянные интегрирования определяются из граничных условий первого рода

. (25)

Подставляя постоянные интегрирования в формулу (24), получим уравнение распределения температуры в рассматриваемом сечении стенки

. (26)

Из выражения (26) следует, что уравнение распределение температуры в стенке, при граничных условиях первого рода, является линейной функцией.

По закону Фурье и с учетом формул (23) и (25) получим

. (27)

Тепловой поток определяется следующим образом:

. (28)

Отношение называется тепловой проводимостью стенки. Обратная величина представляет собой удельное термическое сопротивление стенки.

С учетом выше сказанного уравнения (27) и (28) могут быть представлены следующим образом:

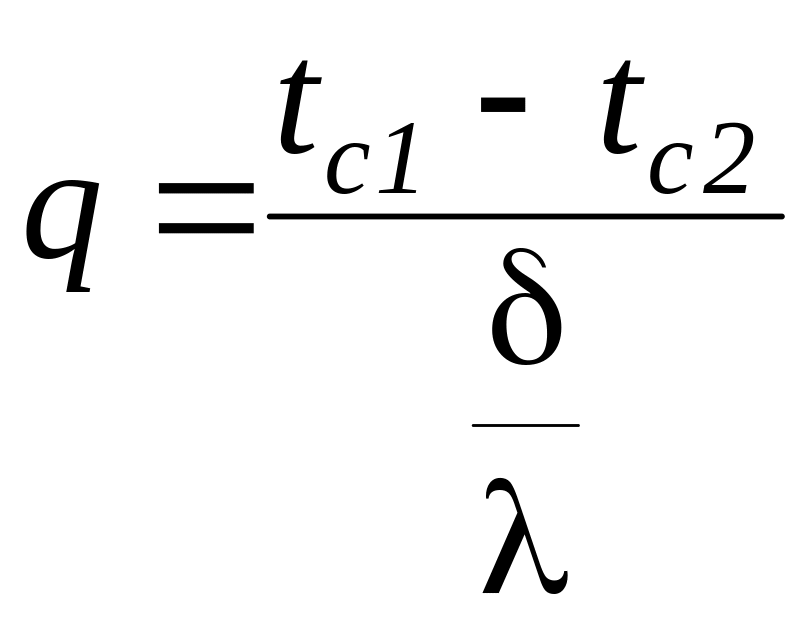, (29)

. (30)

Таким образом можно утверждать, что величина удельного или полного теплового потока зависит от термического сопротивления стенки.

Рассмотрим передачу тепла теплопроводностью через плоскую трехслойную стенку (рис. 2б) при условиях: толщина слоев стенки , , ;

коэффициенты теплопроводности материалов соответственно , , ; контакт между стенками идеальный и температура на границе смежных слоев одинакова. Перенос тепла происходит в стационарных условиях – плотность теплового потока по всем слоям стенки имеет одно и то же значение (q=const.). В этих условиях

(31)

Выделим из этого ряда равенств разности температур (падение температуры по слоям стенки):

(32)

(32а)

(32б)

Складывая левые и правые части уравнений разности температур, получаем слева изменение температуры в стенке , справа – произведение плотности теплового потока q и общего термического сопротивления

(33)

Таким образом, для плотности теплового потока при переносе теплоты теплопроводностью через плоскую трехслойную стенку получим следующее выражение:

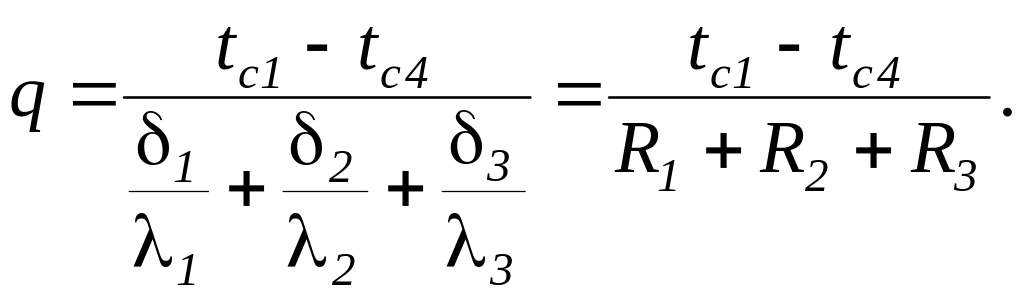(34)

В общем случае для плоской стенки, состоящей из n – слоев, это выражение запишется так

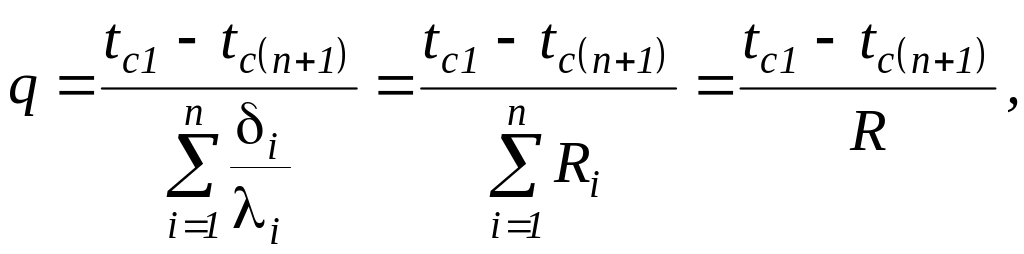(35)

где R – общее термическое сопротивление многослойной стенки.

Как следует из соотношения (35), плотность теплового потока прямо пропорциональна разности температур ( ) и обратно пропорциональна термическому сопротивлению стенки R.

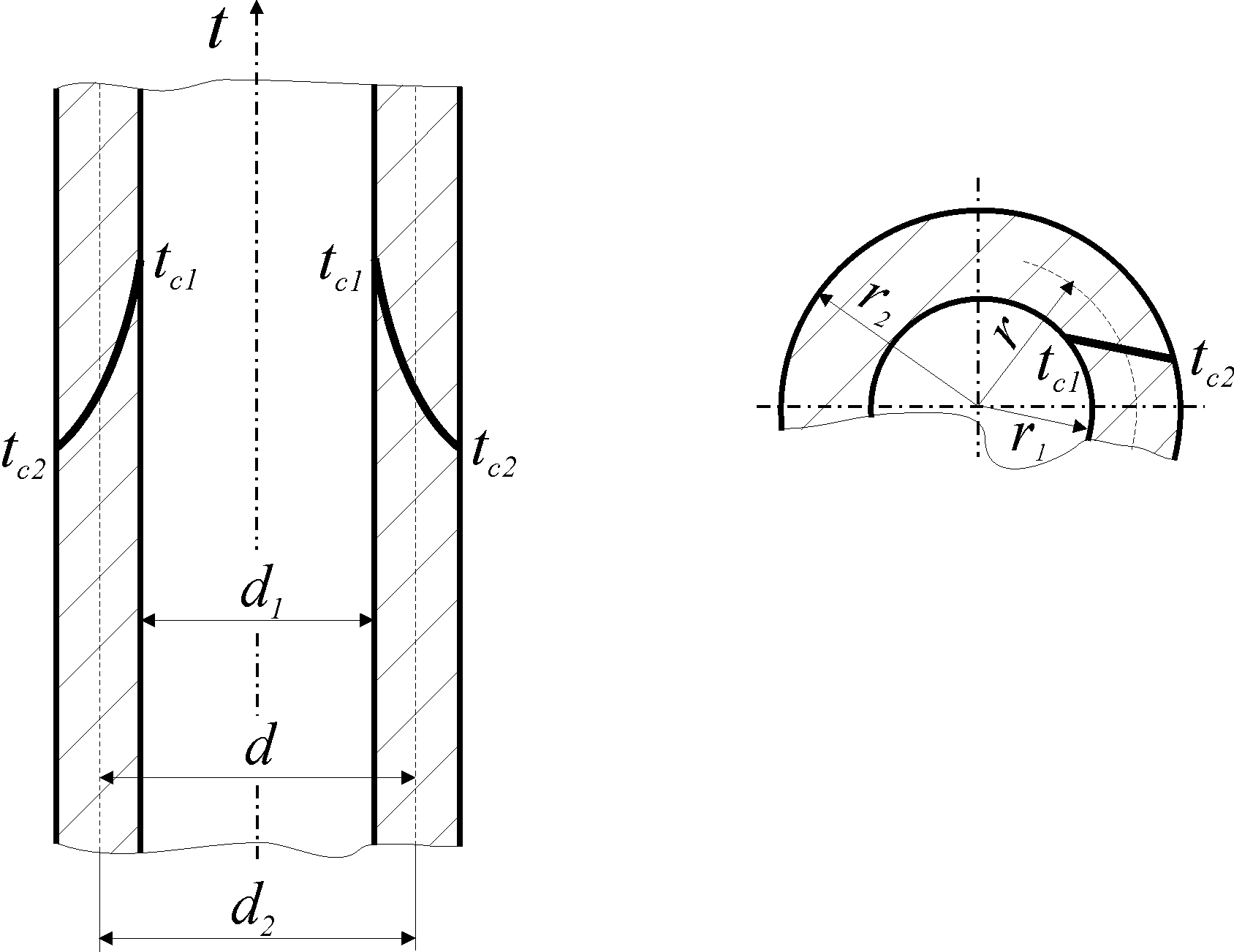
Рис.3. Теплопроводность цилиндрической стенки

Теплопроводность цилиндрической стенки

Рассмотрим теплопроводность цилиндрической однослойной стенки (рис. 3) с внутренним диаметром d₁=2r₁ и наружным диаметром d₂=2r₂ в условиях стационарного температурного поля . Внутренние источники теплоты отсутствуют (q_v=0).

Уравнение теплопроводности цилиндрической стенки (14) в рассматриваемых условиях имеет вид

=0. (36)

Температуры на наружной и внутренней поверхности цилиндрической стенки неизменны и ось z совмещена с осью цилиндра

и . (36а)

В данном случае температура изменяется только в радиальном направлении

. (37)

Граничные условия

при _,

при _. (38)

Для решения уравнения (37) введем новую переменную , тогда уравнение (37) запишется в виде

. (39)

Интегрируя (39), получим

. (40)

Потенцируя выражение (40) и переходя к первоначальным переменным, получаем

. (41)

После интегрирования имеем

. (42)

Постоянные интегрирования С₁ и С₂ можно определить из граничных условий (38):

; . (43)

Решая уравнение (43) относительно С₁ и С₂, найдем:

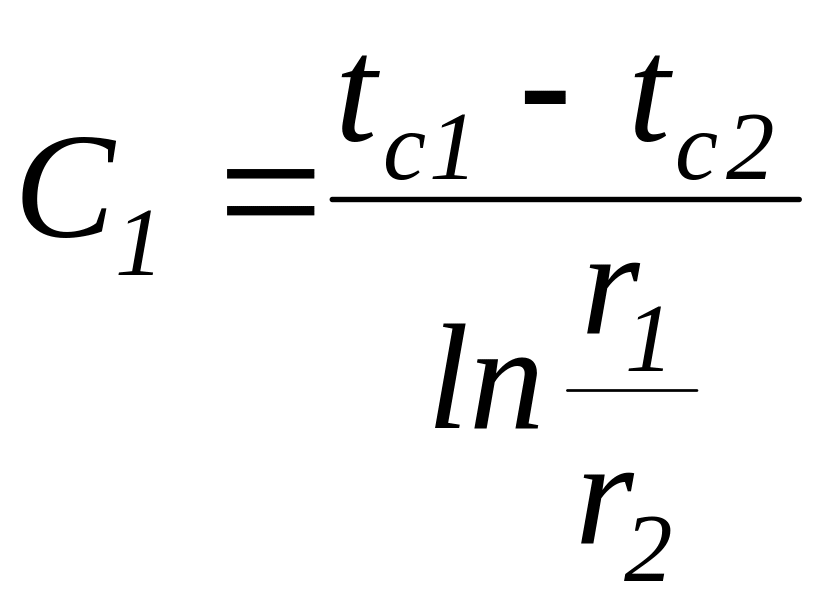; . (43а)

Подставляя полученные значения С₁ и С₂ в уравнение (42), получаем

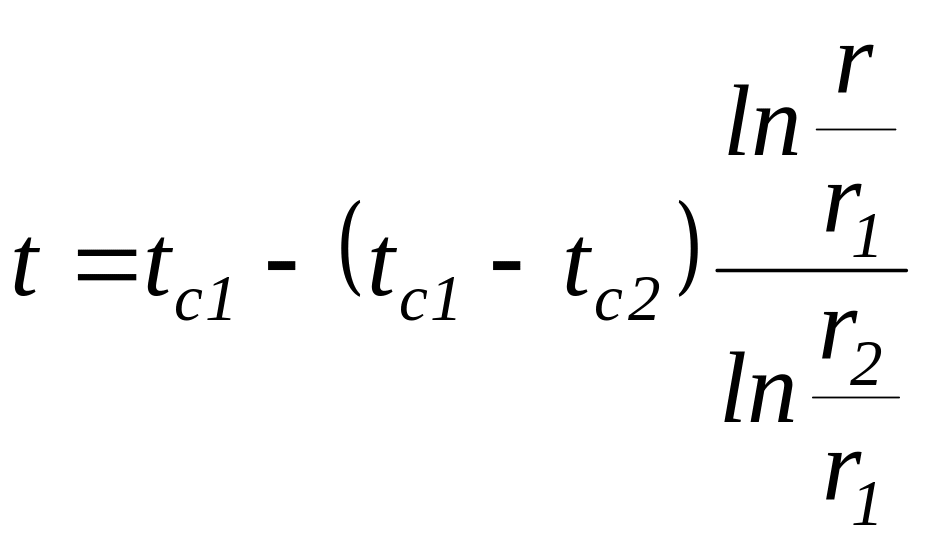. (44)

Выражение температурного поля (44) представляет собой уравнение логарифмической кривой. То, обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим.

В случае плоской стенки плотность теплового потока q остается одинаковой для всех изотермических поверхностей.

В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность будет величиной переменой, так как величина поверхности зависит от радиуса.

Для определения теплового потока через цилиндрическую поверхность воспользуемся законом Фурье

. (45)

Подставляя в уравнение Фурье значение градиента температуры (41) получим (учитывая, что )

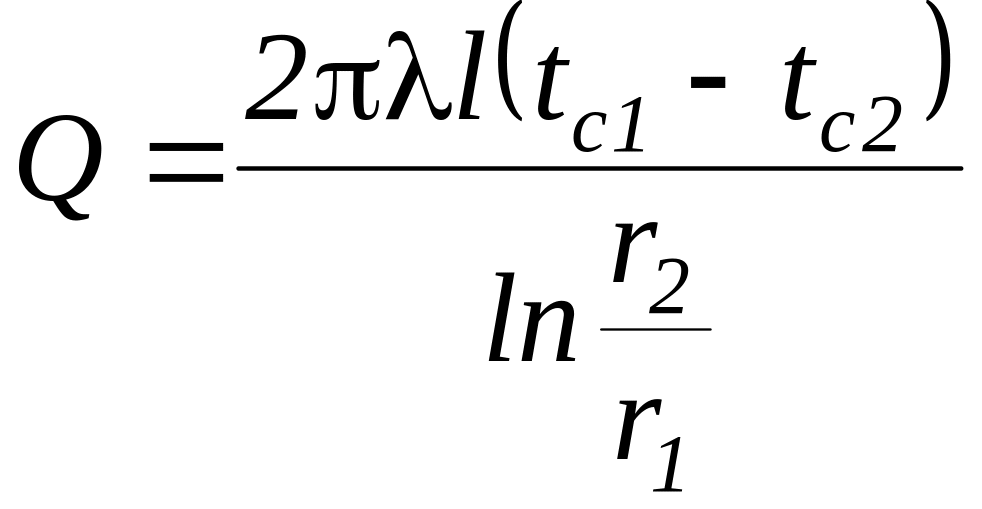, (46)

или

. (46а)

Тепловой поток может быть отнесен либо к единице внутренней или внешней поверхности, либо к единице длины. При этом расчетные соотношения для удельного теплового потока принимают вид

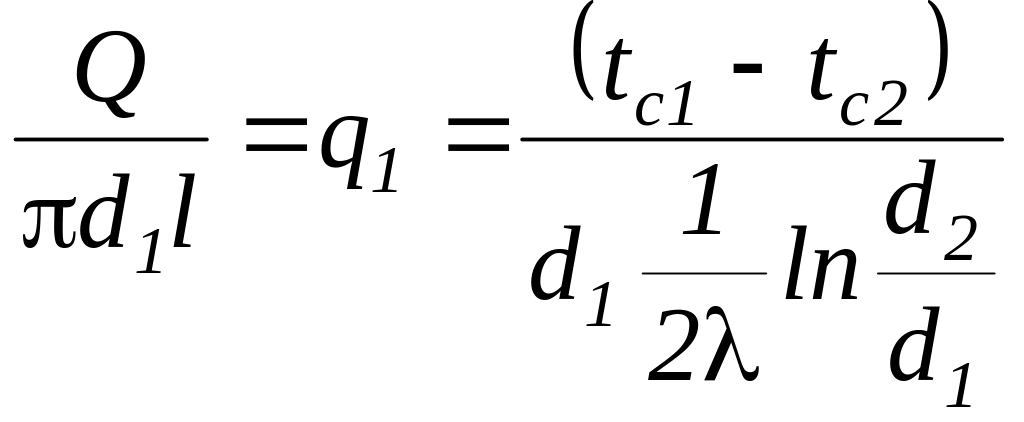, (47)

(q₁ – тепловой поток через единицу внутренней поверхности);

, (48)

(q₂ – тепловой поток через единицу внешней поверхности);

, (49)

(q_l – тепловой поток через единицу длины поверхности).

Тепловой поток отнесенный к единице длины, имеет размерность Вm/м и называется линейным тепловым потоком.

Рассуждая аналогично, как при получении расчетного соотношения теплового потока для многослойной плоской стенки, можно получить выражение для определения линейного теплового потока в случае многослойной цилиндрической стенки

. (50)

где знаменатель называется полным термическим сопротивлением теплопроводности многослойной цилиндрической стенки.

Из уравнения (50) может быть определена температура на границе любых двух слоев

. (51)

Теплопроводность криволинейной стенки

При передаче теплоты через произвольные криволинейные стенки тепловой поток определяется по такому же уравнению, как и для плоской стенки, только в выражение вводится расчетная поверхность теплопередачи

(52)

Расчетная поверхность теплопроводности принимается в зависимости от вида стенки, через которую происходит передача теплоты (для плоской стенки поверхности равны; для цилиндрической стенки средняя расчетная поверхность определяется как средняя логарифмическая; для сферической как средняя геометрическая) :

для плоской стенки

Для цилиндрической стенки

Для сферической стенки

Тепловой поток через многослойные криволинейные стенки определяется по уравнению

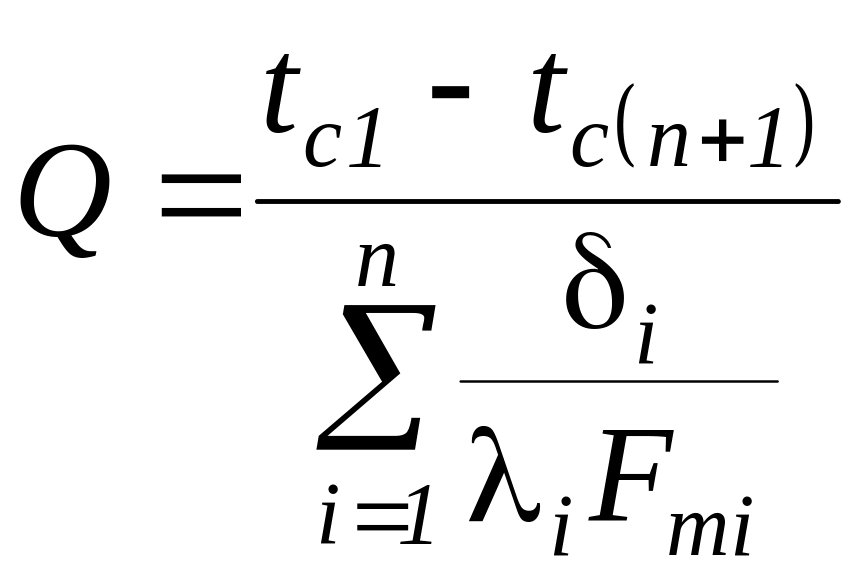, (53)

где – толщина, коэффициент теплопроводности и расчетная поверхность рассматриваемого слоя.

Уравнения (52) и (53) называются обобщенными уравнениями стационарной теплопроводности.

Подставляя в уравнения (52) или (53) значения средних поверхностей можно получить уравнение теплопроводности для плоской, цилиндрической или сферической стенки.