
- •Б.П. Поршаков, а.Ф. Калинин, с.М. Купцов, а.С. Лопатин, к.Х. Шотиди
- •Часть II Теплопередача
- •Введение
- •Основные положения теплообмена
- •2. Теплопроводность при стационарном температурном поле
- •3. Теплопроводность при нестационарном температурном поле
- •4. Основные положения конвективного теплообмена
- •4. Теплообмен при естественной конвекции
- •6. Теплообмен при вынужденном движении жидкости
- •7. Теплообмен при кипении однокомпонентной жидкости
- •8. Теплообмен при конденсации чистого пара
- •9. Теплообмен при конденсации пара из парогазовой смеси
- •10. Лучистый теплообмен
- •11. Сложный теплообмен (теплопередача)
- •12. Тепловой расчет теплообменных аппаратов
11. Сложный теплообмен (теплопередача)
Процесс передачи теплоты от одной среды (теплоносителя) к другой среде (теплоносителю) через разделяющую их стенку называется теплопередачей и состоит из процессов теплоотдачи от горячего теплоносителя к поверхности стенки, передачи теплоты теплопроводностью через многослойную (или однослойную) стенку и процесса теплоотдачи от поверхности стенки к холодному теплоносителю. При установившемся процессе теплопередачи средние температуры горячего и холодного теплоносителей (сред) остаются постоянными вдоль поверхности стенки, а тепловой поток сохраняет неизменное значение (Q = const.).
Расчетная формула стационарного процесса теплопередачи имеет следующий вид:
![]() ,
(191)
,
(191)
где Q – тепловой поток;
k – коэффициент
теплопередачи; F –
поверхность теплопередачи;
![]() =
(tm1
– tm2)
– средний температурный напор (средняя
разность температур).
=
(tm1
– tm2)
– средний температурный напор (средняя
разность температур).
Коэффициент теплопередачи k выражает количество передаваемого количества теплоты в единицу времени через единицу поверхности при температурном напоре равном 1 градусу.
В большинстве случаев при движении теплообменивающих жидкостей вдоль поверхности теплообмена их температуры изменяются. Коэффициент теплопередачи также изменяется по поверхности теплообмена.
Однако во многих случаях можно рассматривать величину коэффициента теплопередачи постоянной по всей поверхности теплообмена, а разность температур между жидкостями принимать средней по поверхности теплообмена.
В этом случае для определения теплового потока имеем
![]() .
(192)
.
(192)
Коэффициент теплопередачи имеет очень важное прикладное значение. В зависимости от принятой схемы расчета теплопередачи величина к относится к единице поверхности или длины стенки. Расчетные формулы для определения коэффициента теплопередачи в том или другом случае, а также формулы для определения среднего температурного напора (средней разности температур) рассматриваются ниже.
Теплопередача чрез плоскую стенку,
Рассмотрим процесс передачи теплоты
через плоскую стенку поверхностью F,
толщиной
![]() и
коэффициентом теплопроводности
,
при известных температурах горячего
и
коэффициентом теплопроводности
,
при известных температурах горячего
![]() и холодного теплоносителя
и холодного теплоносителя
![]() ,
а также коэффициентов теплоотдачи от
горячего
,
а также коэффициентов теплоотдачи от
горячего
![]() и холодного
и холодного
![]() теплоносителей (рис. 21 ). Температура на
внешних поверхностях стенки неизвестны.
теплоносителей (рис. 21 ). Температура на
внешних поверхностях стенки неизвестны.
При стационарном температурном поле системы тепловой поток и плотность теплового потока постоянны. Поэтому на основе законов Фурье и Ньютона можно написать:
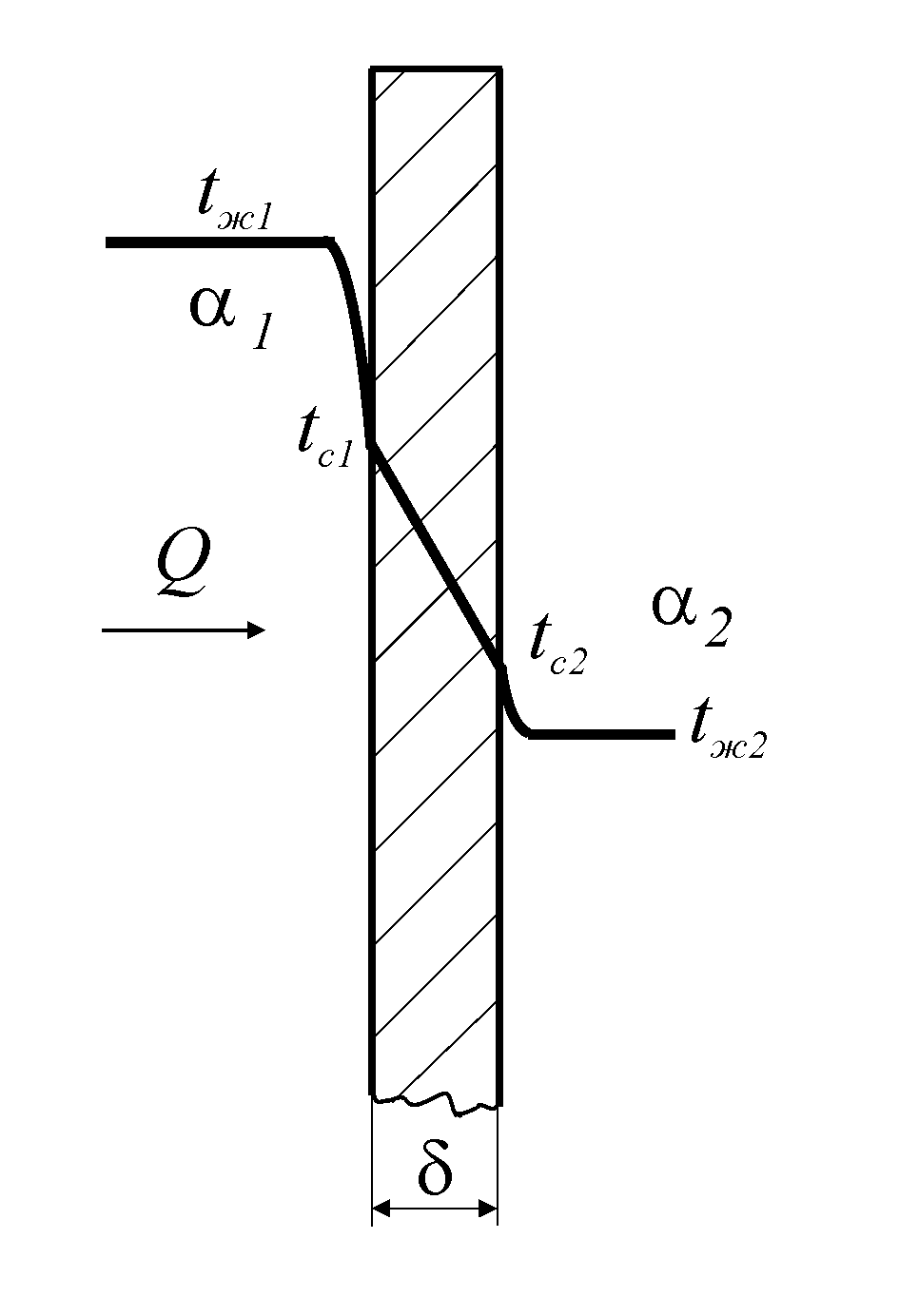 тепловой
поток, передаваемый от горячего
теплоносителя к единице поверхности
стенки
тепловой
поток, передаваемый от горячего
теплоносителя к единице поверхности
стенки
![]() ,
(193)
,
(193)
то же самый тепловой поток передается теплопроводностью через стенку
Рис. 21. Теплопередача через
однослойную плоскую стенку![]()
и передается от поверхности стенки к холод-ному теплоносителю
![]() (195)
(195)
Решая эти уравнения относительно разности температур, находим:
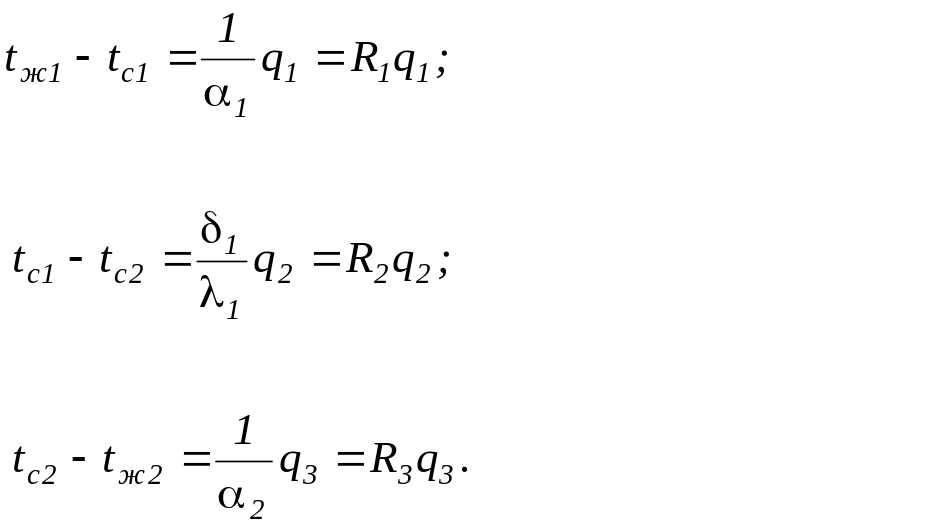 (196)
(196)
Складывая по частям выражения разностей
температур и учитывая, что
![]() получим выражение для итоговой разности
температур
получим выражение для итоговой разности
температур
![]() (197)
(197)
где
![]() – термическое сопротивление теплопередачи
плоской стенки (м2К\Bm);
– термическое сопротивление теплопередачи
плоской стенки (м2К\Bm);
![]()
![]() ;
;![]() – термические сопротивления теплоотдачи
со стороны горячего теплоносителя,
теплопроводности плоской стенки и
термические сопротивления теплоотдачи
со стороны холодного теплоносителя
соответственно.
– термические сопротивления теплоотдачи
со стороны горячего теплоносителя,
теплопроводности плоской стенки и
термические сопротивления теплоотдачи
со стороны холодного теплоносителя
соответственно.
Отсюда, следует выражение для плотности теплового потока и теплового потока (уравнение теплопередачи плоской стенки):
![]() (198)
(198)
![]() ,
(198а)
,
(198а)
где k=1/R – коэффициентом теплопередачи плоской стенки (Вт/м2 К)
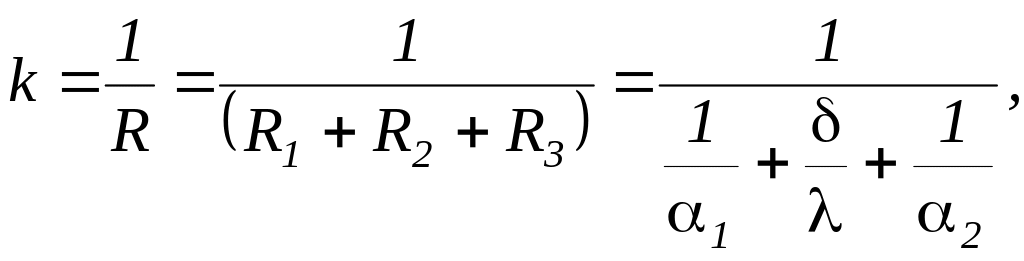 (199)
(199)
После определения количества передаваемой теплоты (Q, q) по формуле (191) можно найти температуры на поверхностях стенки из выражений разности температур:
![]() ;
(200)
;
(200)
![]() (201)
(201)
В
Рис. 22. Теплопередача через однослойную
плоскую стенку
т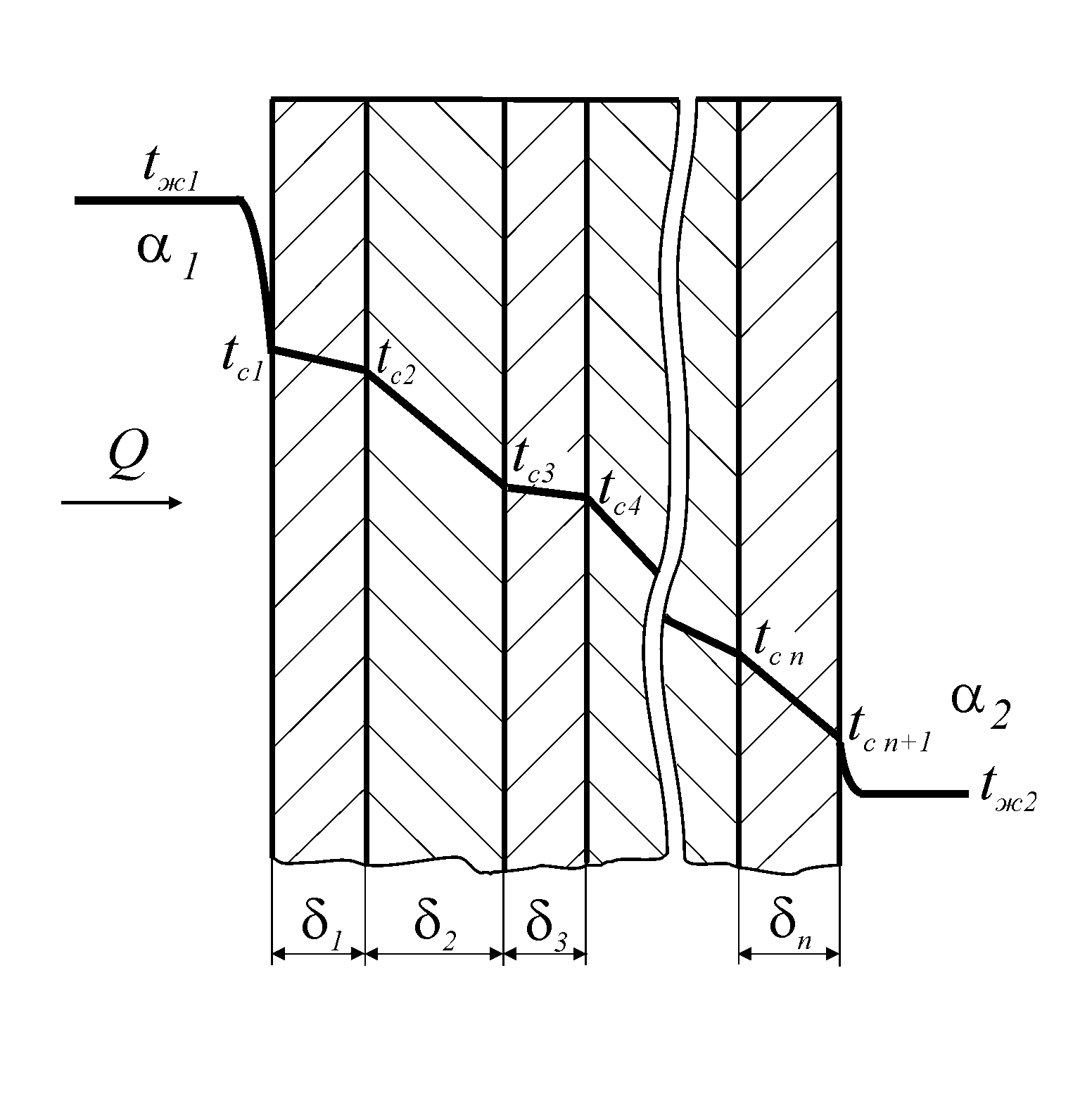 ермическое
сопротивление и следовательно коэффициент
теплопередачи определяются с учетом
термических сопротивлений каждого слоя
ермическое
сопротивление и следовательно коэффициент
теплопередачи определяются с учетом
термических сопротивлений каждого слоя
Рис. 21. Теплопередача через
многослойную плоскую стенку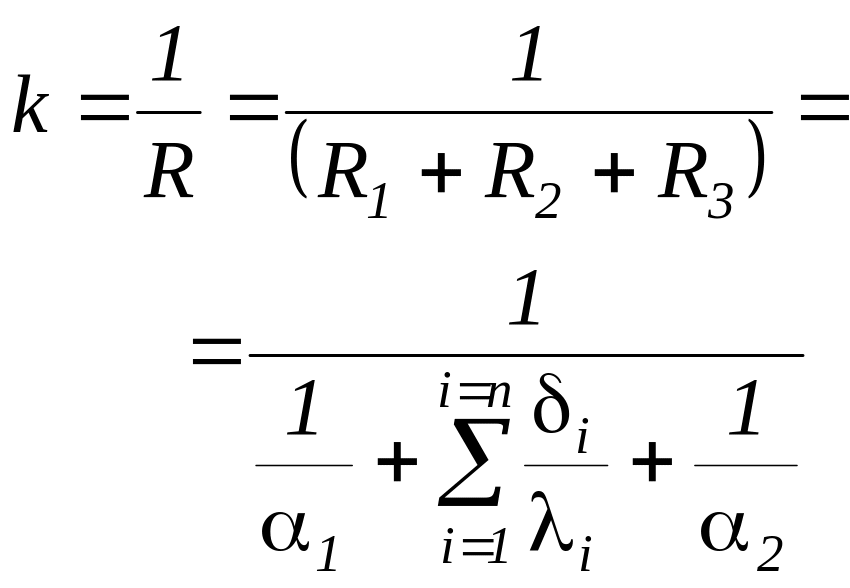
Температура поверхности и на стыке слоев определяется из тех же соображений, что и для однослойной стенки
 (203)
(203)
Теплопередача через цилиндрическую стенку
Рассмотрим передачу теплоты через
однородную стенку трубы длиной l
c внутренним диаметром
d1 и
внешним диаметром d2
(рис. 23). Коэффициент теплопроводности
материала стенки трубы λ. Внутри трубы
движется горячий теплоноситель со
средней температурой tж1,
с наружи – холодный теплоноситель со
средней температурой tж2.
Температуры стенки на внутренней
поверхности tс1,
наружной поверхности tс2
неизвестны. Коэффициенты теплоотдачи
со стороны горячего и холодного
теплоносителя равны
![]() и
и
![]() соответственно
соответственно
При стационарном температурном поле системы тепловой поток (Q) постоянен. Поэтому на основе законов Фурье и Ньютона можно написать:
Тепловой поток, передаваемый от горячего теплоносителя к поверхности стенки
![]() ,
(204)
,
(204)
т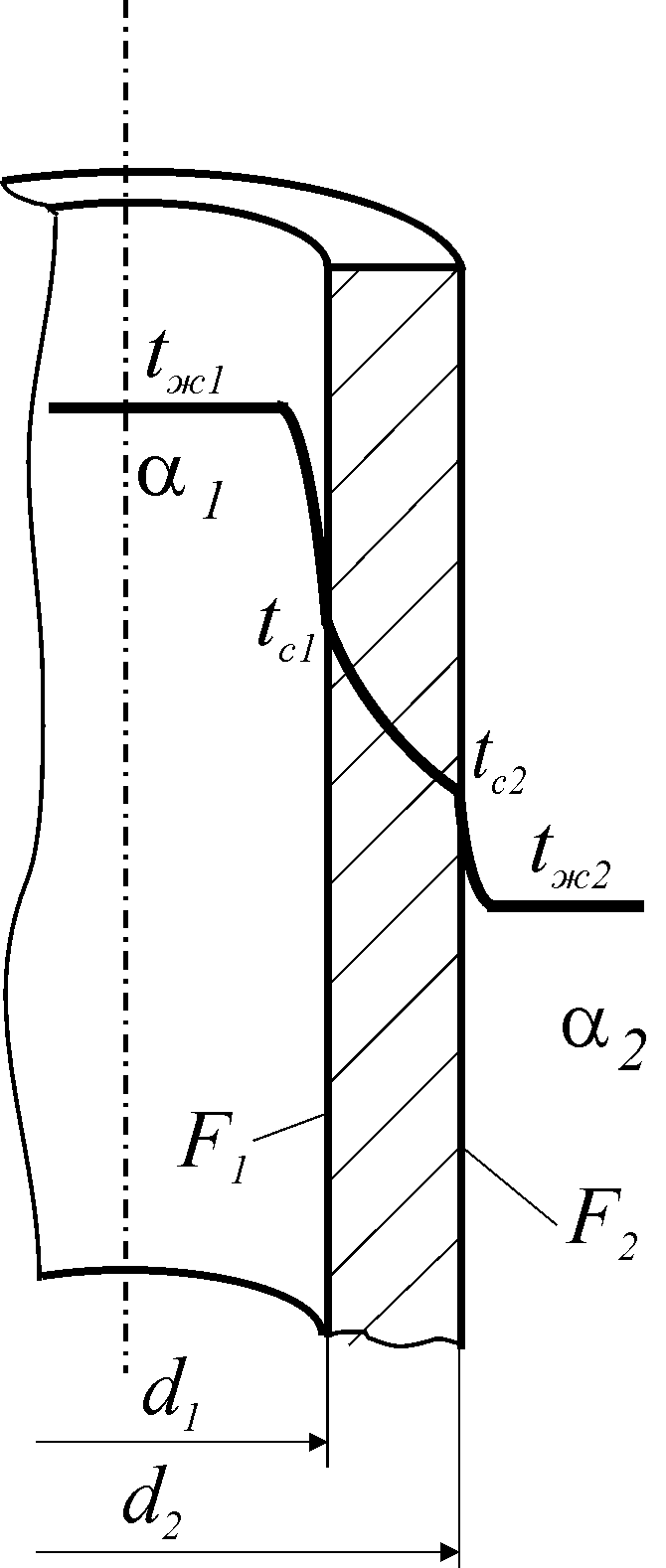 от
же самый тепловой поток передается
от
же самый тепловой поток передается
теплопроводностью через стенку
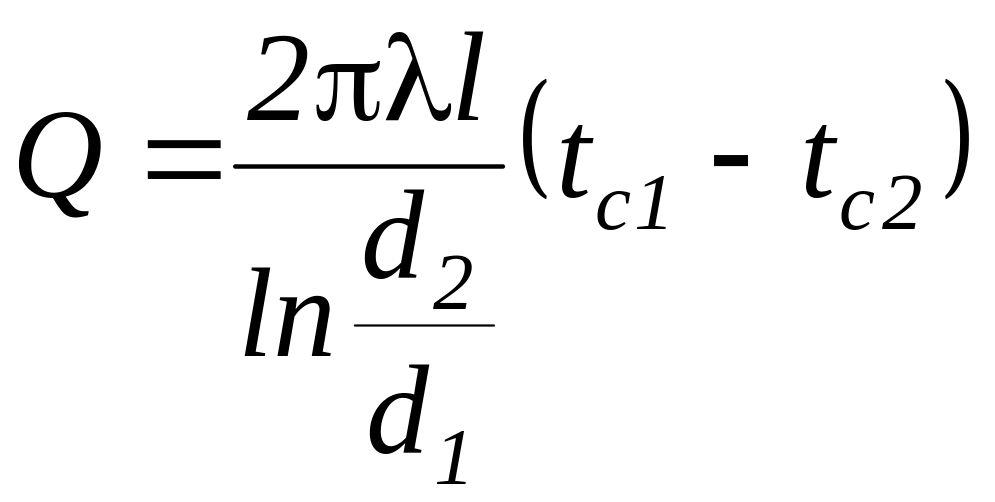 ,
(205)
,
(205)
и передается от поверхности стенки к холодному теплоносителю
![]() (206)
(206)
Рис. 23. Теплопередача через цилиндрическую
стенку
Решая уравнения (204, 205 и 206) относительно разности температур и суммируя
полученные выражения, получим расчетное уравнение для определения Q
![]() ,
(207)
,
(207)
где kl – линейный коэффициентом теплопередачи для цилиндрической однородной стенки, (Вт/м К)
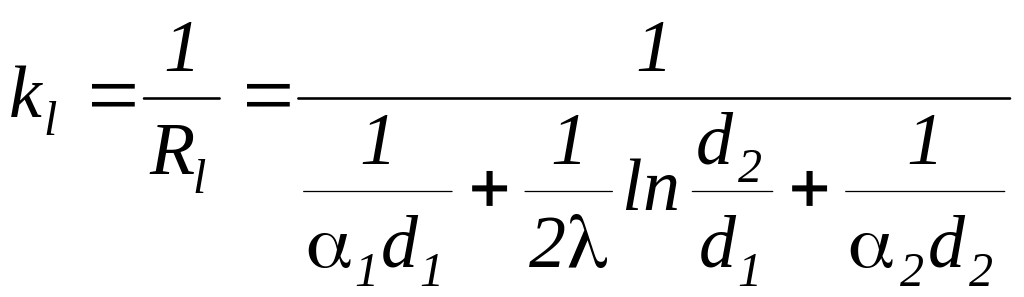 ,
(208)
,
(208)
где
![]() – линейное термическое сопротивление
теплопередачи, (м۟К/Вт)
– линейное термическое сопротивление
теплопередачи, (м۟К/Вт)
![]() (209)
(209)
После определения количества передаваемого количества теплоты Q по формуле (205) можно найти температуры на поверхности стенки
![]() (210)
(210)
В случае многослойной стенки состоящей из n слоев тепловой поток и плотность теплового потока определяются по уравнениям аналогичным однослойной (207) за исключением того, что линейное термическое сопротивление определяются с учетом термических сопротивлений каждого слоя.
Линейное термическое сопротивление теплопередачи многослойной цилиндрической стенки с числом разнородных слоев n определяется по формуле
![]() (211)
(211)
Уравнение теплопередачи для криволинейной поверхности
Для криволинейных стенок (рис. 24) произведение kF неразделимо, для определения теплового потока можно воспользоваться уравнением теплового
потока для плоской стенки (198), для этого водится понятие средней поверхности каждого слоя стенки (Fmi)
![]() ,
(212)
,
(212)
где KF – неразделимый комплекс называемый водяным эквивалентом поверхности теплопередачи
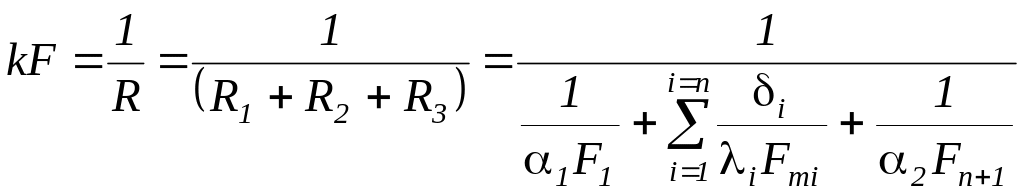 ,
(213)
,
(213)
г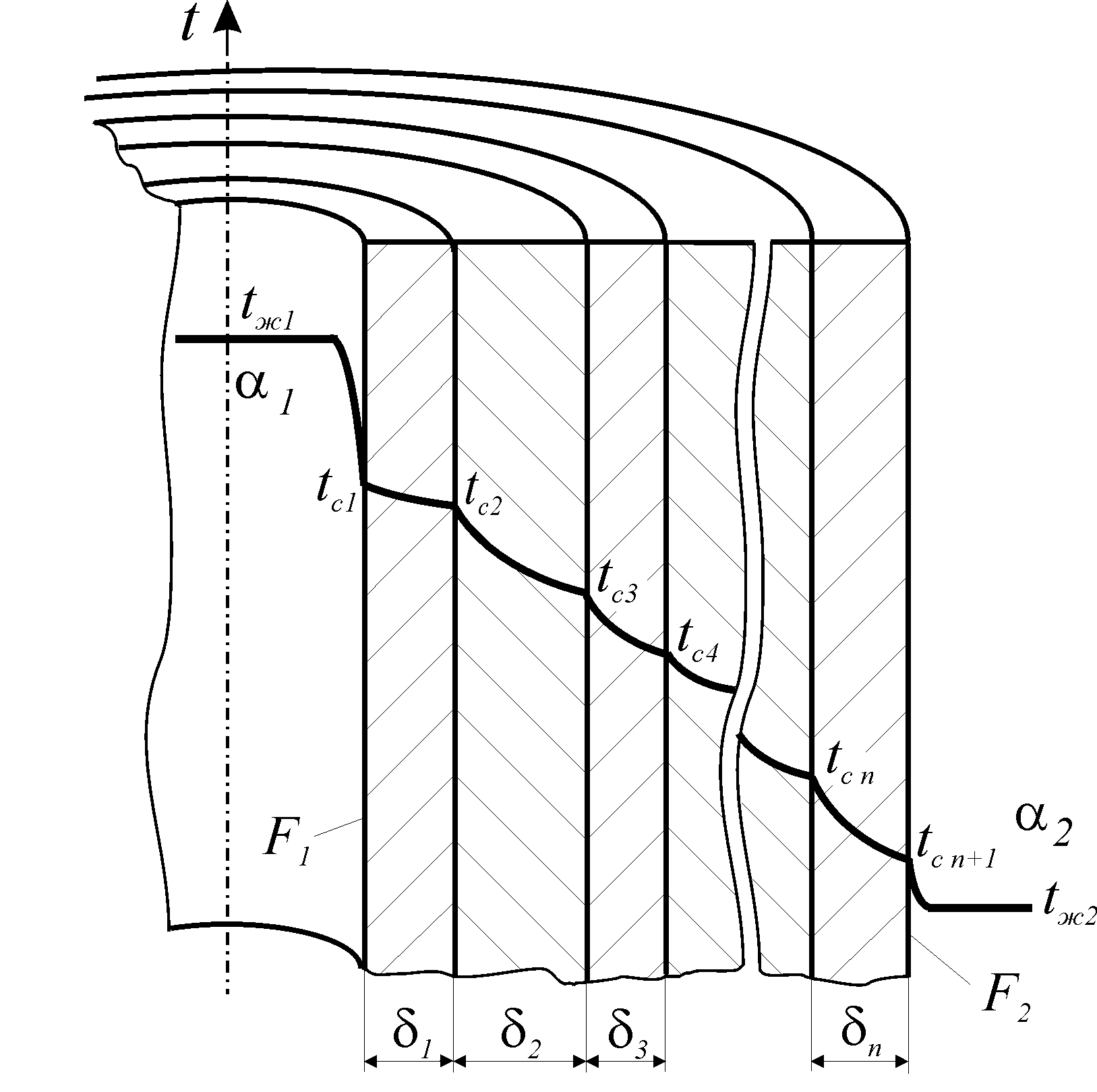 де
Fmi
– средняя поверхность теплопередачи,
в частном случае определяемая:
де
Fmi
– средняя поверхность теплопередачи,
в частном случае определяемая:
для плоской стенки
![]() – средняя арифметическая поверхность
(справедлива также и для тонкостенных
цилиндрических систем),
– средняя арифметическая поверхность
(справедлива также и для тонкостенных
цилиндрических систем),
для цилиндрической поверхности
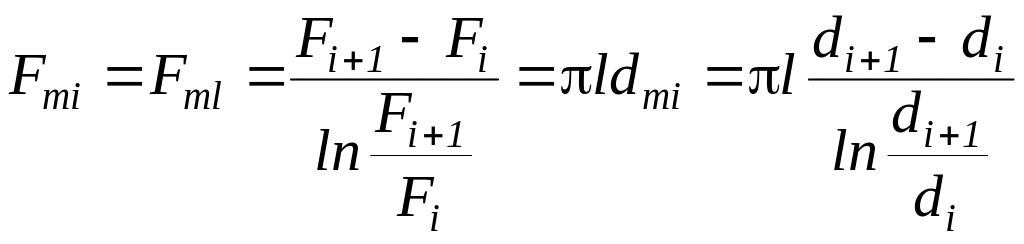 – средняя логарифмическая поверхность,
– средняя логарифмическая поверхность,
д
Рис. 24. Теплопередача через
криволинейную поверхность.![]() – средняя геометрическая поверхность.
– средняя геометрическая поверхность.
Расчетная поверхность теплопередачи для криволинейных стенок определяется из выражения
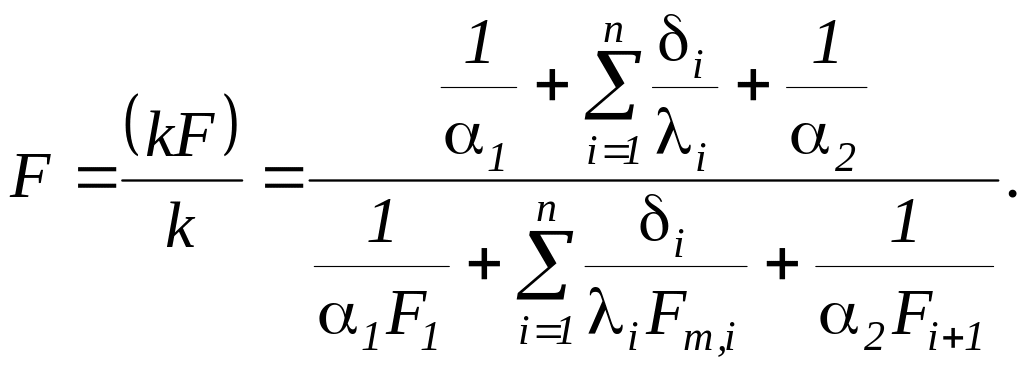 (214)
(214)
Если термическое сопротивление стенки мало и α1 > α2, то k ≈ α2 и F=F2; если α2 > α1, то k ≈ α1 и F=F1.
В технических расчетах чаще всего приходится решать проблему двух видов: уменьшение тепловых потерь (изоляция поверхности теплообмена) и увеличение количества передаваемого тепла (интенсификация теплопередачи).
Изоляция криволинейных поверхностей теплообмена имеет свои особенности.
Рассмотрим покрытие изоляцией однослойной цилиндрической стенки. Линейное термическое сопротивление стенки (211) перепишется следующим образом:
![]() (215)
(215)
Из последнего уравнения видно, что при увеличении толщины изоляции d3 термическое сопротивление Rlu = 1/(2λи)lnd3/d2 увеличивается, а термическое сопротивление Rl2= 1/(α2d3) уменьшается; термические сопротивления Rl1= 1/(α1d1) и Rlc = 1/(2λc)lnd2/d1 сохраняют постоянное значение. При этом суммарное термическое сопротивление Rl сначала уменьшается, а затем увеличивается, а удельный линейный тепловой поток ql в соответствии с предыдущим уравнением, наоборот, сначала возрастает, а потом уменьшается. Диаметр изоляции, при котором суммарное термическое сопротивление имеет минимальное значение, а удельный линейный тепловой поток максимальное, называется критическим (d3 = dкр) и определяется по формуле
![]() (216)
(216)
При наложении изоляции на трубу поступают следующим образом: выбрав какой-либо теплоизоляционный материал по известным α2 и λu рассчитывают dкр. Если окажется, что dкр > d2 , то применение выбранного материала в качестве тепловой изоляции нецелесообразно. Таким образом, для эффективного применения тепловой изоляции необходимо, чтобы dкр ≤ d2, а λu ≤ α2d2/2.
Из выражения (![]() )
следует, что чем больше q, тем больше
тепловой поток, т. е. задача интенсификации
теплообмена сводится к увеличению
удельного теплосъема. Увеличить q
можно путем повышения ∆t
и k. Увеличение ∆t
может быть связано с изменением технологии
процесса, что не всегда возможно; кроме
того, увеличение ∆t
всегда влечет возрастание энергетических
затрат и повышение q в этих условиях
в каждом конкретном случае решается на
основе технико-экономических расчетов.
Увеличить k можно за счет повышения
коэффициентов теплоотдачи. При этом,
как уже говорилось, при большом различии
α1 и α2 коэффициент
теплопередачи всегда меньше минимального
α. Таким образом, увеличить k и
интенсифицировать теплообмен можно
двумя путями: при α1 << α2
или
)
следует, что чем больше q, тем больше
тепловой поток, т. е. задача интенсификации
теплообмена сводится к увеличению
удельного теплосъема. Увеличить q
можно путем повышения ∆t
и k. Увеличение ∆t
может быть связано с изменением технологии
процесса, что не всегда возможно; кроме
того, увеличение ∆t
всегда влечет возрастание энергетических
затрат и повышение q в этих условиях
в каждом конкретном случае решается на
основе технико-экономических расчетов.
Увеличить k можно за счет повышения
коэффициентов теплоотдачи. При этом,
как уже говорилось, при большом различии
α1 и α2 коэффициент
теплопередачи всегда меньше минимального
α. Таким образом, увеличить k и
интенсифицировать теплообмен можно
двумя путями: при α1 << α2
или
α2 << α1 – повышением меньшего коэффициента теплоотдачи; при α1 ≈ α2 – повышением обоих коэффициентов или любого из них.
Помимо увеличения коэффициентов теплоотдачи интенсифицировать процесс теплопередачи можно за счет оребрения поверхности теплоотдачи. Оребряется та поверхность, со стороны которой α меньше; теоретическим пределом оребрения является равенство термических сопротивлений теплоотдачи 1/( α1F1) = 1/(α2F2) в итоге увеличивается произведение kF и повышается Q.
Теплопередача при изменяющихся температурах вдоль поверхности теплообмена
В теплообменных аппаратах и теплоиспользующих устройствах температура греющего и нагреваемого теплоносителей изменяются вдоль поверхности теплообмена: температура греющего теплоносителя понижается, а температура нагреваемого повышается. Исключение составляют теплообменные аппараты, в которых с одной стороны поверхности испаряется жидкость или конденсируется пар(например испарители или конденсаторы).
В условиях изменяющихся температур теплоносителей уравнение теплопередачи можно записать в следующем виде:
![]() ,
(217)
,
(217)
Тепловой поток передаваемый через всю поверхность теплообмена при постоянном коэффициенте теплопередачи k равен
![]() (218)
(218)
Для учета изменения температур
теплоносителей по поверхности теплообмена
в расчетное уравнение теплопередачи
вводится средняя разность температур
(средний температурный напор)
![]() ,
который определяется уравнением
,
который определяется уравнением
![]() ,
(219)
,
(219)
где - средняя разность температур.
Из сопоставления уравнений 218 и 219 следует
![]() (220)
(220)
Уравнение 220 называют уравнением теплопередачи для теплообменных аппаратов (обобщенное уравнение теплопередачи)
Вид расчетного соотношения для средней разности температур (219) существенно зависит от взаимного направления греющего и нагреваемого теплоносителей. Различают следующие направления движения теплоносителей в рекуперативных теплообменниках: прямоток, противоток, перекрестный ток, смешанный ток.
На рис. 25 показаны схемы движения теплоносителей и изменение температур теплоносителей при прямотоке и противотоке.
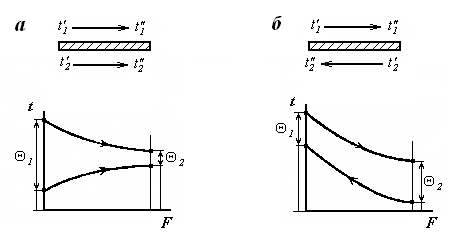
Рис. 25. График изменения температуры теплоносителей
при прямотоке (а) и противотоке (б)
В процессе теплообмена греющий теплоноситель отдает некоторое количество теплоты (Q1), нагреваемый теплоноситель получает такое же количество теплоты (Q2) (теоретический процесс, без потерь теплоты в окружающую среду). Пренебрегая падением давления теплоносителей при движении, т.е. считая процесс протекающим изобарным, из первого начала термодинамики имеем
![]() ,
(221)
,
(221)
где Q – мощность
теплообменного аппарата, Вт;![]() и
и
![]() – расход горячего и холодного
теплоносителей соответственно, кг\с;
– расход горячего и холодного
теплоносителей соответственно, кг\с;
![]() и
и
![]() – удельное изменение энтальпии греющего
и нагреваемого теплоносителей
соответственно, Дж\кг.
– удельное изменение энтальпии греющего
и нагреваемого теплоносителей
соответственно, Дж\кг.
Для конвективных теплообменных аппаратов
(в процессе теплообмена отсутствуют
фазовые переходы) в силу того, что
![]() имеем
имеем
![]() ,
(222)
,
(222)
где cpm1
и cpm2
– средние теплоемкости горячего и
холодного теплоносителей; W1=G1cpm1
и W2=G2cpm2
– водяные эквиваленты горячего и
холодного теплоносителей;
![]() ;
;
![]() (рис. 25).
(рис. 25).
Уравнения (221 и 222) называются уравнениями теплового баланса теплообменного аппарата (ТА).
В силу того, что для теоретического процесса теплопередачи в ТА, тепловой поток определенный из уравнение теплового баланса (222) равен тепловому потоку определенному по уравнению теплопередачи (220) имеем
![]() (223)
(223)
Расчетные соотношения для определения средней разности температур простейших схем взаимного движения теплоносителя: прямотока и противотока (рис. 25) получаются из выражения (223) записанного для элементарного участка теплообмена
![]() ,
(224)
,
(224)
где
![]() – текущая средняя разность температур
(текущий температурный напор).
– текущая средняя разность температур
(текущий температурный напор).
Знаки в уравнении элементарного теплового потока (224) определяются принятым направлением движения теплоносителей: верхние знаки относятся к прямотоку, а нижние – к противотоку.
Выделим из исходного дифференциального уравнения (224) изменения температуры для горячего и холодного теплоносителей
![]() (224а)
(224а)
Выразим разность изменения температур горячего и холодного теплоносителей
![]() ,
(224б)
,
(224б)
где Wm
– приведенный водяной эквивалент обоих
потоков,
![]() .
.
Окончательно имеем следующее преобразованное выражение теплопередачи на элементарном участке
![]() (225)
(225)
Разделив переменные в уравнении (225) и его проинтегрировав получим первое интегральное уравнение
![]() .
(226)
.
(226)
Второе интегральное уравнение получается при непосредственном интегрировании уравнения теплопередачи (225)
![]() (227)
(227)
Сопоставляя уравнения (226 и 227) получим расчетное уравнение для средней разности температур
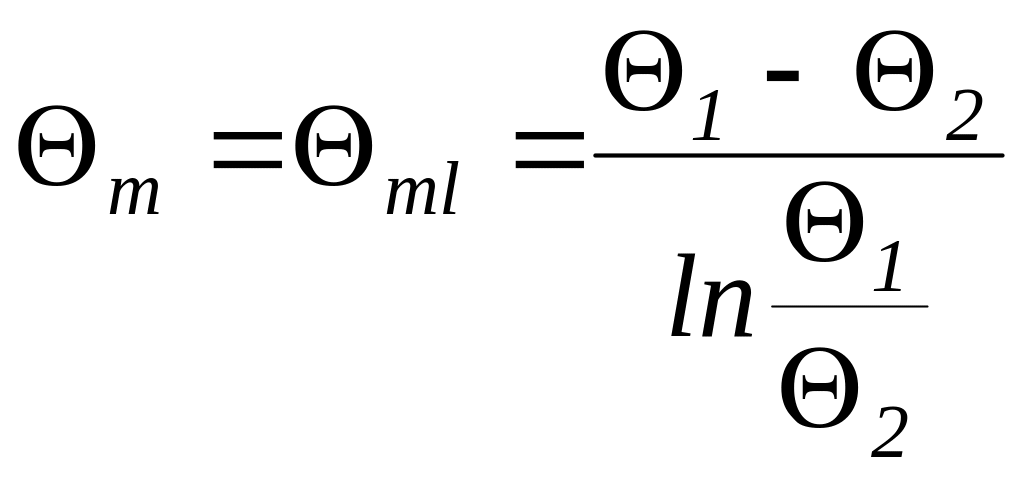 ,
(228)
,
(228)
где
![]() и
и
![]() - начальная и конечная разности температур
соответственно.
- начальная и конечная разности температур
соответственно.
Расчетное уравнение средней разности температур (228), справедливое для схем прямотока и противотока, называется среднелогарифмической разностью температур или уравнением Грасгофа.
Начальная и конечная разность температур для схемы прямотока и противотока определяются по следующим соотношения (рис. 25):
для схемы прямоток
![]() ;
;
![]() ,
(228а)
,
(228а)
для схемы противоток
![]() ;
;
![]() (228б)
(228б)
При незначительном изменении температуры теплоносителей вдоль поверхностей теплообмена вместо среднелогарифмической разности температур можно пользоваться среднеарифметической разностью температур
![]() (229)
(229)
Среднеарифметическая разность температур
всегда больше среднелогарифмической,
но при
![]() они отличаются друг от друга менее 3%,
что вполне допустимо в технических
расчетах.
они отличаются друг от друга менее 3%,
что вполне допустимо в технических
расчетах.
Точное определение среднелогарифмической разности температур для схем с перекрестным и смешанным током теплоносителей связано с большими трудностями. В этом случае удобно пользоваться расчетными графиками, составленными для наиболее распространенных схем теплообменных аппаратов [2, 3, 8, 9].
Предварительно по формуле Грасгофа (228) одсчитывается среднелогарифмическая разность температур для противоточного теплообменного аппарата. Затем вычисляются вспомогательные характеристики R и PS по уравнениям
![]() ,
,
![]() .
(230)
.
(230)
По значениям этих характеристик с учетом схемы движения теплоносителей (число ходов по трубному и межтрубному пространству) из графиков определяется коэффициент t (рис. 3, 4, 5) [2, 3, 8, 9].
Действительная средняя разность температур между теплоносителями для рекуперативных ТА всех типов определяется по соотношению
![]() ,
(231)
,
(231)
где t – коэффициент, учитывающий различие между действительной средней разностью температур (m) и средней логарифмической разностью температур между теплоносителями при противоточной схеме движения теплоносителей (mL).
Обобщенное уравнение теплопередачи при переменных температурах
Наиболее общим уравнением теплопередачи при переменных темпера-
турах , действительным для любых схем движения теплоносителей, является уравнение предложенное проф. Н,И. Белоконем [1, 5]
 ,
(232)
,
(232)
где
![]() – средняя разность температур для любых
схем
– средняя разность температур для любых
схем
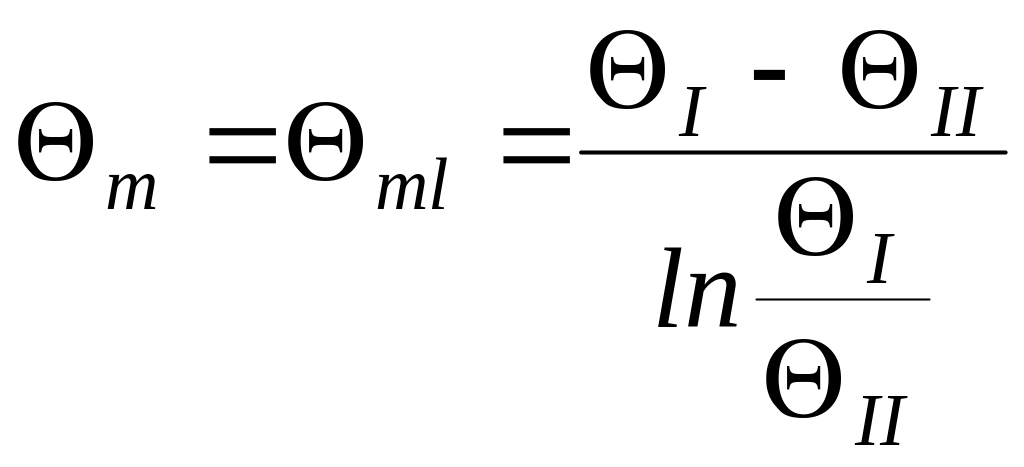 ,
(233)
,
(233)
где
![]() и
и
![]() – начальная и конечная разности
температур теплоносителей
– начальная и конечная разности
температур теплоносителей
![]()
![]() ,
(234)
,
(234)
где
![]() - характеристическая разность температур
- характеристическая разность температур
![]() (235)
(235)
где Wm – приведенный водяной эквивалент теплоносителей,
![]() ;
(236)
;
(236)
Индекс противоточности P
определяется как отношение водяного
эквивалента поверхности теплообмена,
где осуществляется противоточная схема
движения теплоносителей (kF)прот,
и водяного эквивалента поверхности
теплообмена всего ТА (![]() )
[1, 5]
)
[1, 5]
![]() .
(237)
.
(237)
Для прямоточной схемы индекс противоточности равен p = 0, а при противотоке p = 1 и в этом случае уравнение (231) совпадает с уравнением Грасгофа (228).
