10. Лучистый теплообмен

Лучистым теплообменом называется форма распространения между телами в пространстве внутренней энергии. При этом, как отмечалось выше, происходит двойное превращение внутренней энергии, внутренняя энергия тела превращается в лучистую и передается в пространстве путем электромагнитных волн (излучением), в свою очередь, поток энергии электромагнитных волн (лучистая энергия) при поглощении их другим телом вновь превращается во внутреннюю энергию.

Возбудителями электромагнитных волн являются заряженные электроны и ионы. Колебания ионов соответствуют излучению низкой частоты. Излучение вызванное колебаниями электронов может имеет высокую частоту, если электроны входят в состав атомов и молекул. Излучение веществ со свободными электронами имеет импульсный характер с волнами разной частоты, в том числе с волнами низкой частоты.

На волновой характер излучения влияют корпускулярные свойства, которые заключаются в том, что лучистая энергия излучается материальными телами не непрерывно, а отдельными дискретными порциями – квантами света, или фотонами.

Все виды электромагнитного излучения имеют одинаковую природу и отличаются только длиной волны.

Большая часть твердых и жидких тел имеет сплошной спектр излучения, т. е. излучает энергию во всем диапазоне длин волн. Некоторые тела (чистые металлы, газы и др.) излучают энергию только в определенных интервалах длин волн. Такое излучение называется выборочным или селективным.

Количество излучаемой энергии увеличивается с ростом температуры тела, а в газах - с увеличением толщины слоя и давления газа. Для твердых и жидких тел характерно излучение и поглощение лучистой энергии тонким поверхностным слоем. В газах излучение и поглощение энергии происходит всем объемом.

Некоторые виды излучения обладают свойством превращаться в тепловую энергию при поглощении телами, вызывая нагревание. Это свойство излучения определяется длиной волны и, зависит от температуры тела. В наибольшей мере такими свойствами обладает видимое инфракрасное (тепловое) излучение с длиной волны от 0,8 до 800 мк.

Количество энергии, излучаемое поверхностью тела во всем интервале длин волн (от λ=О до λ=∞) в единицу времени, называется полным (интегральным) лучистым потоком Q (Вт). Излучение, соответствующее узкому интервалу длин волн, называется монохроматическим. Лучистый поток, исходящий с единицы поверхности излучающего тела по всем направлениям полупространства называется плотностью интегрального излучения E (Вт/м²)

(157)

Из уравнения (157) следует, что лучистый поток , исходящий со всей поверхности излучающего тела равен

(158)

Плотность интегрального излучения, отнесенная к рассматриваемому диапазону длин волн, называется спектральной интенсивностью излучения (Вт/м³)

(159)

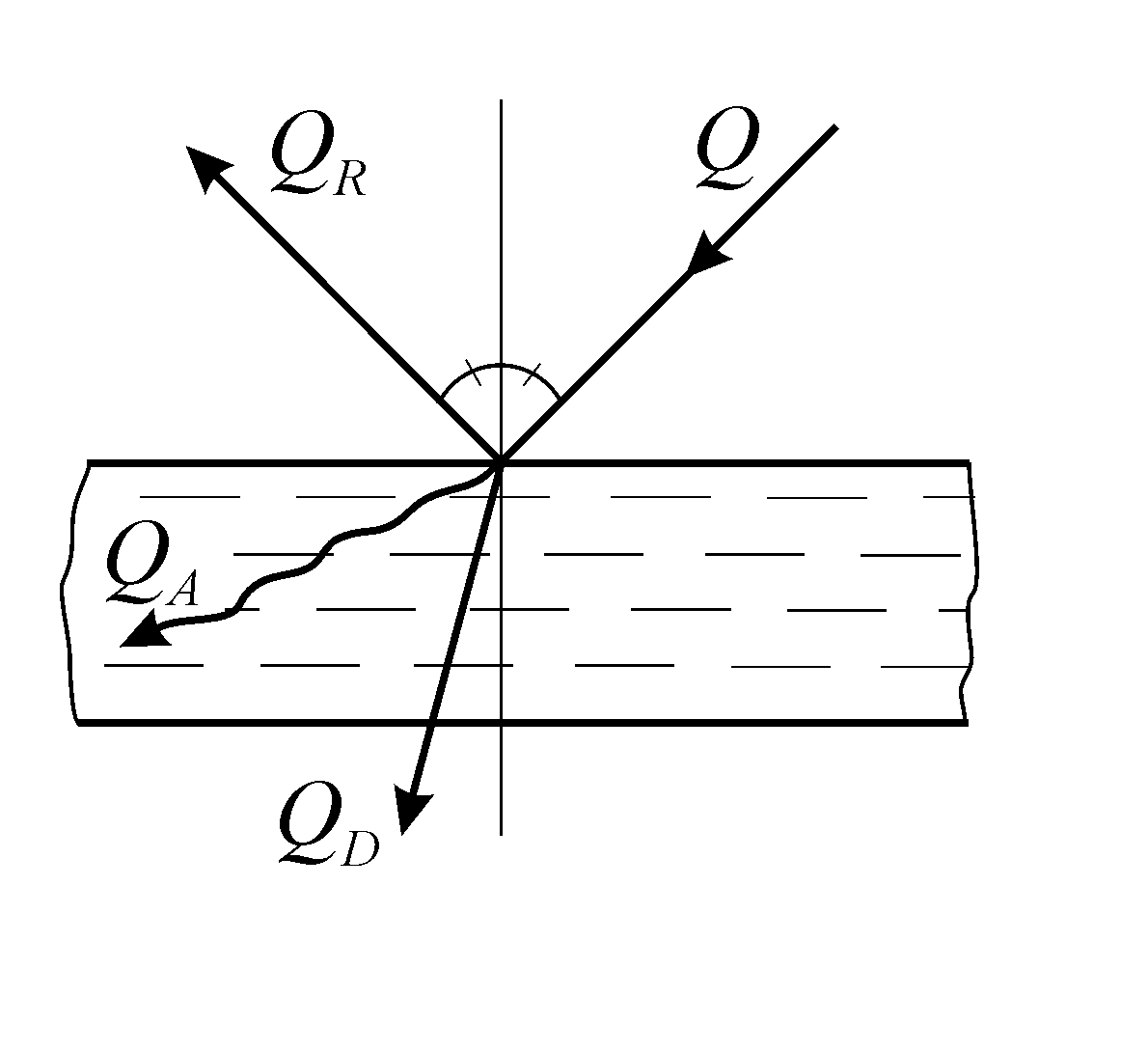
Рис. 16. Распределение лучистого потока падающего на тело

Лучистый поток, падающий на тело Q, частично им поглощается Q_A, частично отражается Q_R, частично проходит сквозь тело Q_D (рис. 16. )

Q = Q_A + Q_R + Q_D. (160)

Разделив обе части равенства на Q и обозначив Q_A/Q=A; Q_R/Q=R, получим:

1 = A+R+D. (161)

Коэффициенты А, R, D характеризуют соответственно поглощательную, отражательную и пропускную (прозрачность) способности тела. В связи с этим они именуются коэффициентами поглощения, отражения и пропускания. Эти коэффициенты для различных тел могут меняться от 0 до 1.

Тела, которые всю падающую на них лучистую энергию поглощают, Q_A=Q и А=l (R=D=0), называются абсолютно черными. Тело, которое всю падающую на него лучистую энергию отражает, Q_R=Q; R=1 (А=D =О), называют абсолютно белым или зеркальным. Тело, которое всю падающую на него лучистую энергию пропускает, Q_D=Q; D=1 (А=R=О), называют абсолютно прозрачным. В природе абсолютно черных, белых и прозрачных тел не существует.

Законы лучистого теплообмена

Закон Планка устанавливает зависимость между спектральной интенсивностью излучения абсолютно черного тела и абсолютной температурой тела. Под спектральной интенсивностью излучения (интенсивностью излучения) понимают отношение плотности полусферического излучения тела к рассматриваемому диапазону длин волн

Планк установил, что изменение интенсивности излучения по длинам волн для абсолютно черного тела подчиняется следующему закону

(162)

где – интенсивность излучения абсолютно черного тела, Вт/м³;

с₁ = 3,74·10^-16 Вт·м² – первая постоянная Планка; - длина волны, м ; с₂=0,0144 м·К – вторая постоянная Планка.

Рис. 17. Спектральная интенсивность абсолютно черного тела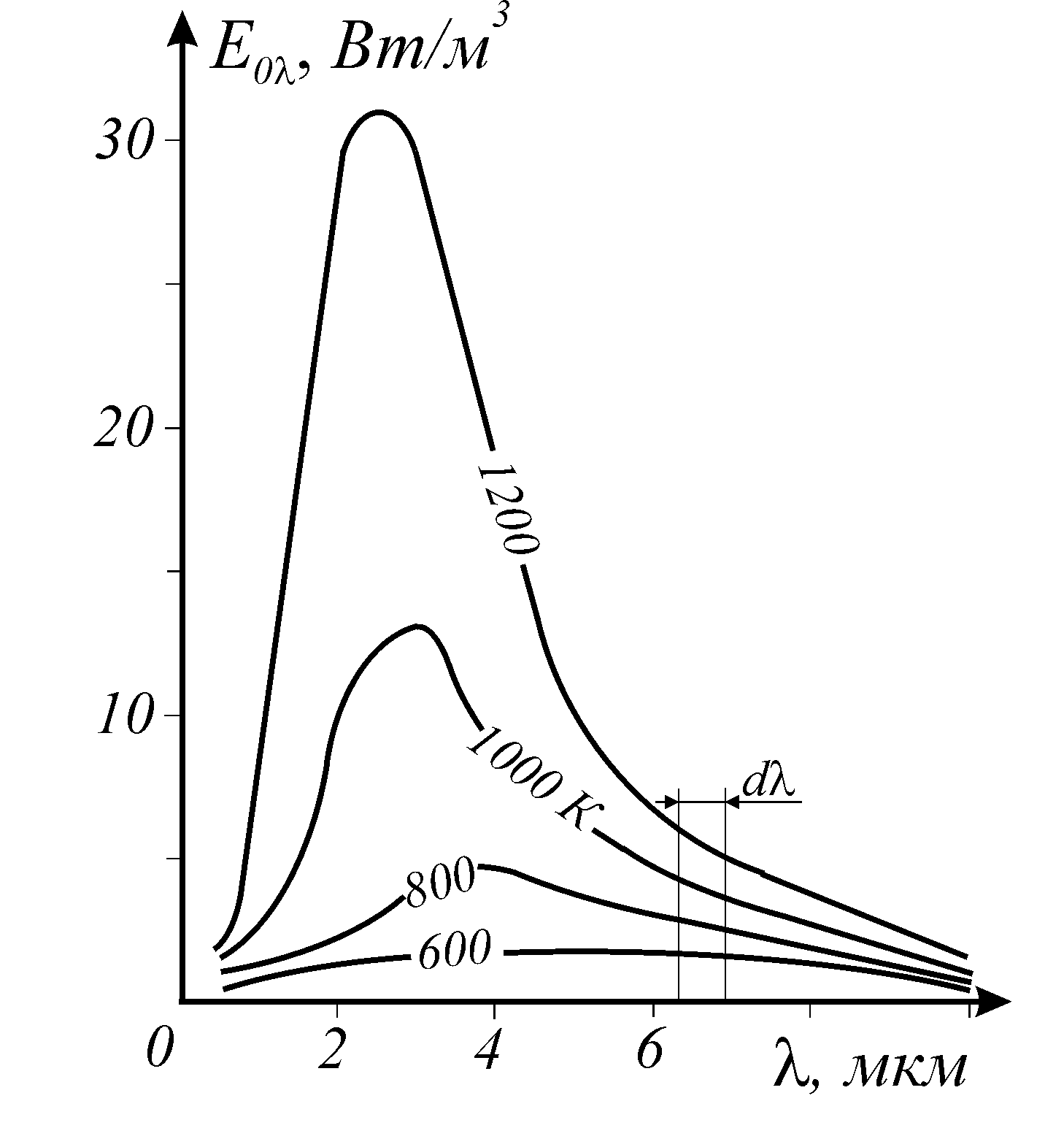

Из приведенных на рис. 17 изотерм видно, что интенсивность излучения на участке коротких волн быстро возрастает до максимума, а затем медленно убывает. При одной и той же длине волны интенсивность излучения тем больше, чем выше температура тела. Каждому значению температуры тела соответствует вполне определенное значение длины волны, при котором излучается максимальное количество энергии.

Закон Вина устанавливает связь ме

жду температурой и длиной волны на которую приходится максимум интенсивности излучения. Максимум интенсивности излучения с ростом температуры тела смещается в сторону более коротких длин волн

, мм (163)

3акон Стефана - Больцмана устанавливает связь между плотностью полусферического интегрального излучения абсолютно черного тела и абсолютной температурой тела. Плотность излучения абсолютно черного тела прямо пропорциональна абсолютной температуре в четвертой степени

(164)

где σ₀, c₀ – коэффициенты пропорциональности (постоянные излучения);

σ₀ = 5,76·10^-8 Вт/( м² ·K⁴); c₀ = 5,76 Вт/(м² ·K⁴).

Для серых тел закон Стефана-Больцмана записывается в виде

, (165)

где с – коэффициент излучения серого тела.

Численные значения с для конкретных тел определяются опытным путем.

Сопоставление плотностей излучения серого и абсолютно черного тел при одинаковой температуре приводит к характеристике, называемой степенью черноты ε

(166)

где – степень черноты тела или относительная излучательная способность или, которая меняется от нуля (абсолютно белое тело) до единицы (абсолютно черное тело).

3акон Кирхгофа устанавливает связь между плотностью интегрального полусферического излучения и поглощательной способностью тел

(167)

т.е. отношение плотности полусферического интегрального излучения к поглощательной способности одинаково для всех тел имеющих одинаковую температуру и равно плотности интегрального полусферического излучения абсолютно черного тела при той же температуре

Из сопоставлении уравнений (166 и 167) следует

(168)

Учитывая, что по определению получаем , т.е. поглощательная способность и степень черноты тела численно равны между собой.

Из закона Кирхгофа также следует, что большей плотностью излучения обладают тела с большей поглощательной способностью и наоборот.

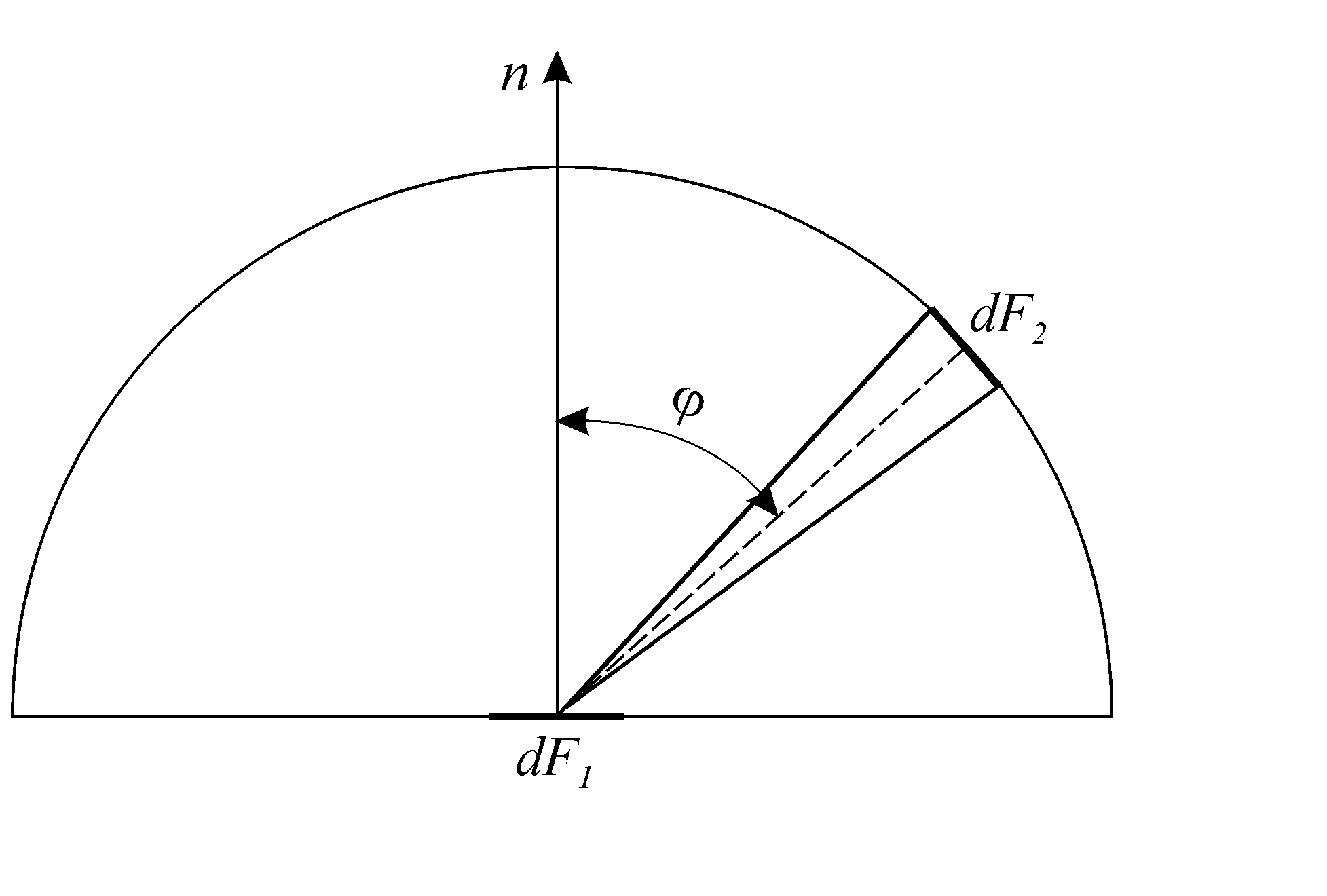
3акон Ламберта устанавливает связь между количеством излучаемой энергии и направлением излучения. Согласно этому закону количество энергии, излучаемое элементом поверхности абсолютно черного тела в направлении элемента поверхности (рис. 18) определяется следующим образом

(169)

г

Рис. 18. К выводу закона Ламберта

де – плотность потока излучения соответствующая углу ; – элементарный телесный угол, под которым из данной точки излучающего тела видна элементарная площадка на поверхности полусферы, имеющей центр в этой точке; – угол меж

ду нормалью к излучающей поверхности и направлением излучения.

Наибольшее значение соответствует направлению нормали к поверхности ( =0). Для реальных тел закон Ламберта выполняется лишь приближенно.

Теплообмен излучением между твердыми телами

в прозрачной среде

На основании законов излучения, можно получить расчетные формулы для лучистого теплообмена между телами. При этом считается, что при теп

лообмене излучение между телами, количество переданной тепловой энергии определяется как разность между количеством энергии, излучаемое телом, и количеством энергии, поглощаемой им от излучения другого тела

Рассмотрим простейший случай теплообмена излучением между двумя плоскопараллельными бесконечными стенками 1 и 2 (рис. 19). Поверхность каждой стенки равна F; стенки имеют постоянные во времени температуры T₁ и T₂; степени черноты на внутренних граничных поверхностях соответственно равны и .

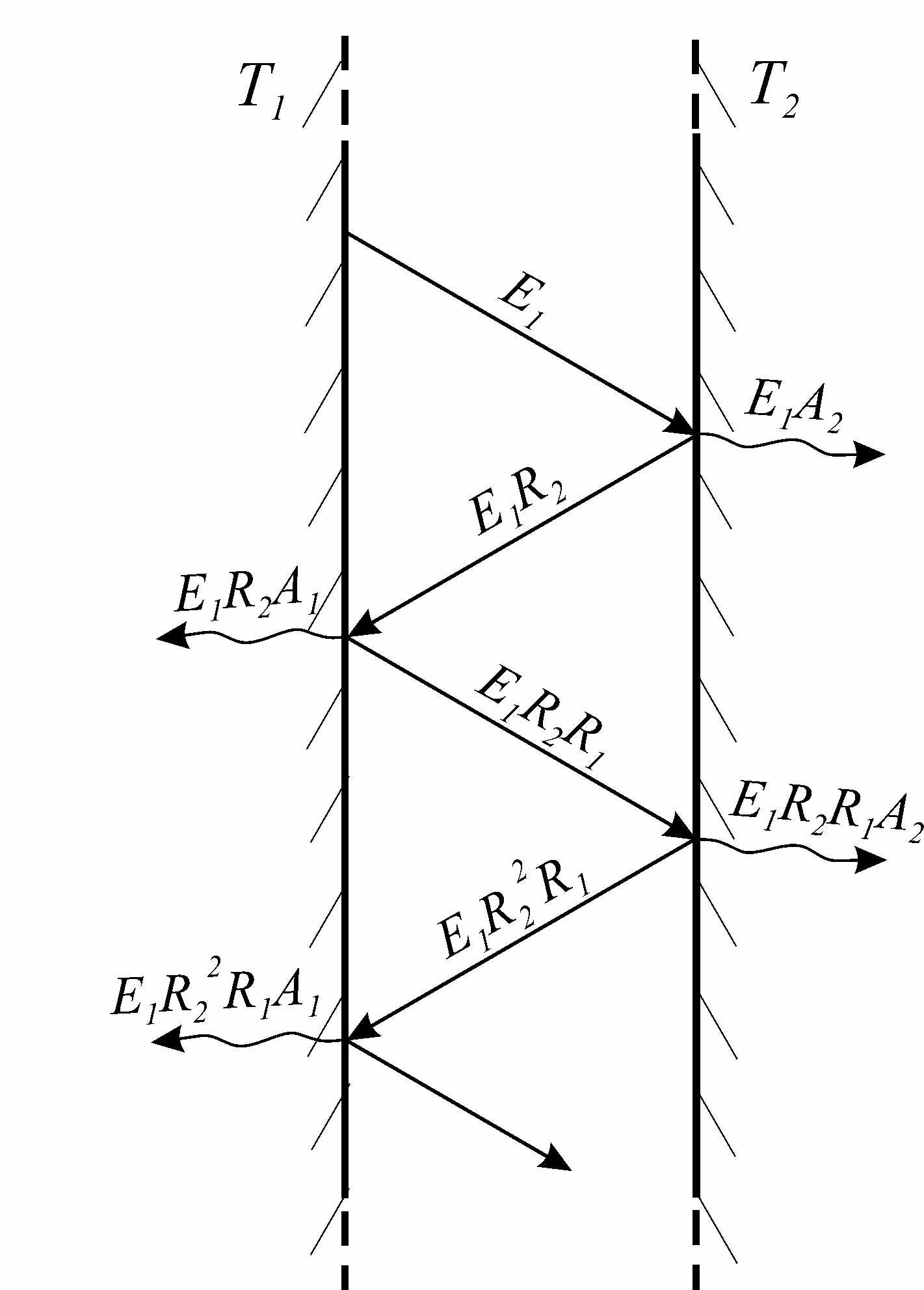П лотность излучения стенки 1 равна ; эта энергия достигает стенки 2 и там поглощается в количестве , а остальное ее

количество отражается обратно на стенку 1.

Д

Рис. 19. Лучистый теплообмен

между твердыми телами

альнейшая судьба этого количества энергии видна из схемы (рис. 19). Поглощаемая стенкой 1 плотность излучения за счет собственного излучения равна сумме бесконечного числа слагаемых

[ ] (170)

Выражение в скобках является убывающей геометрической прогрес-сией. Сумма бесконечного числа ее членов равна

(171)

Поэтому

(172)

Наряду с поглощением энергии первая стенка поглощает еще часть энергии, излучаемой второй стенкой. Вычисление этого добавочного количества поглощаемой энергии аналогично предыдущему

(173)

Таким образом, стенка 1 испускает плотность излучения , а поглощает . Разность между плотностью излучения и поглощением равна тепловому потоку переданного от стенки 1 к стенке 2

(174)

где – общее количество лучистой энергии (эффективное излучение), излучаемое телом 1; – общее количество энергии (эффективное излучение), излучаемое стенкой 2 и падающее на стенку 1.

Эффективное излучение включает в себя собственное излучение , а также отраженное, падающее на стенку 1 от стенки 2,

. (175)

Аналогично получается выражение для эффективного излучения стенки 2 в направлении стенки 1

. (176)

Подставляя выражения для и в уравнение (174), и после преобразования получим

(177)

где Q_1,2 – тепловой поток, передаваемый излучением телом 1 телу 2, Вт;

ε_1,2 – приведенная степень черноты тел 1 и 2, определяемая из выражения

(178)

Уравнение (177) представляет собой расчетную формулу для определения результирующего количества энергии лучистого теплообмена между двумя плоскопараллельными поверхностями.

Аналогично можно получить расчетную формулу для лучистого теплообмена между двумя телами в замкнутом пространстве, когда поверхность одного тела облекает поверхность другого (рис. 20).

Т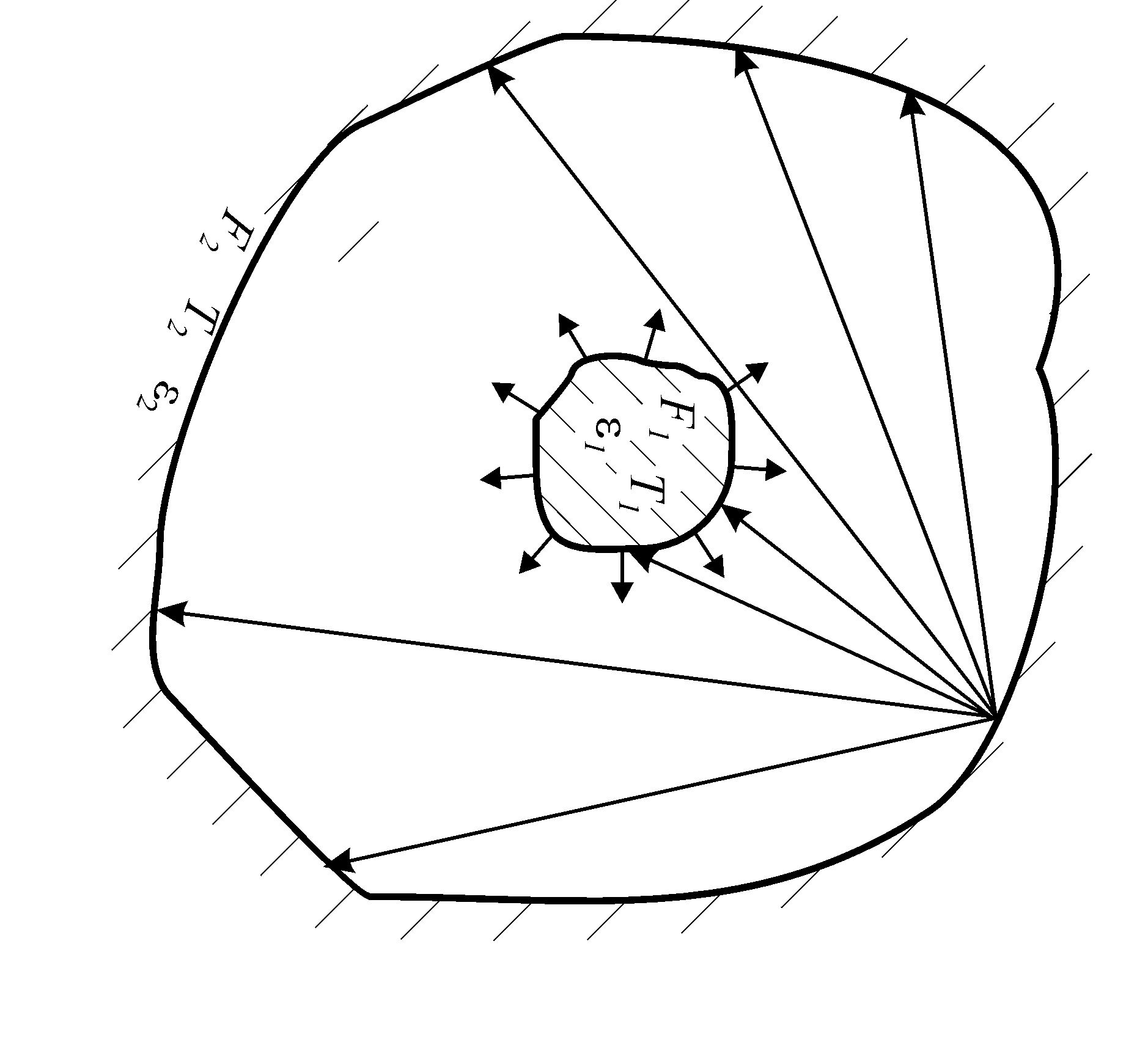 акой случай еще называют теплообменом излучением между телом и его оболочкой; внутреннее тело всегда тело 1.

Суммарные собственные излучения тела и оболочки соответственно равны:

Рис. 20. Теплообмен между телом и окружающей его

оболочкой

; . (179)

Искомая величина Q_1,2 будет результирующим излучением на поверхности тела и внутренней поверхности оболочки

(180)

где – приведенная степень черноты,

(181)

Если поверхность F₁ значительно меньше поверхности F₂,то и расчетная формула принимает вид

(182)

При F₁=F₂ расчетная формула (181) переходит в формулу (178).

Уравнение (180)можно использовать для расчета лучистого теплообмена между двумя телами любой формы и произвольного их расположения, только в каждом частном случае для определения приведенных степени черноты и поверхности (для ε_пр и F) имеются свои расчетные выражения.

Для уменьшения количества лучистой энергии, падающей со стороны других тел на данное тело, необходимо уменьшать температуру тел, излучающих энергию и уменьшать степень их черноты.

При невозможности проведения таких мероприятий или их недостаточной эффективности применяют экраны. Экраны изготовляются из материалов с малой степенью черноты, обычно в виде тонких полированных металлических пластин.

Для оценки эффективности экрана получим расчетное соотношение для определения лучистого теплообмена между телами при наличии экранов. Данное расчетное уравнение получается из решения системы уравнений, каждое из которых характеризует теплообмен между телом 1 и экраном и экраном и телом 2

(183)

где – приведенная степень черноты при наличии экранов

(184)

Установка одного экрана между двумя параллельными стенками уменьшает теплообмен излучением примерно в 2 раза, в общем случае при установке n экранов (степени черноты тел и экранов равны) лучистый теплообмен уменьшается в раз.

Теплообмен излучением между ограждающей поверхностью

и газами

Излучение газов имеет свои особенности и законы. Одно- и двухатомные газы являются прозрачными; излучают и поглощают энергию трех- и многоатомные газы (СО₂, Н₂О, SО₂, NH₃ и др.). Спектр излучения и поглощения трех- и многоатомных газов является селективным (избирательным), т. е. эти газы излучают и поглощают в определенных интервалах длин волн, называемых полосами. Так, у углекислого газа имеются три основные полосы: первая полоса в интервале длин волн от λ₁ = 2,36 мкм до λ₂ = 3,02 мкм, вторая полоса от λ₁ = 4,01 мкм до λ₂ = 4,8 мкм и третья полоса от λ₁ = 12,5 мкм до λ₂ = 16,5 мкм. В отличие от твердых тел излучение и поглощение энергии газами происходит не в их поверхностном слое, а во всем объеме.

По мере прохождения лучистого потока через объем многоатомных газов его энергия вследствие поглощения непрерывно уменьшается. Это ослабление зависит от природы газа, его температуры и числа молекул, находящихся на пути луча. Число молекул пропорционально толщине слоя газов 1 и плотности газа (парциальному давлению р_i) . Излучение газов существенно отклоняется от излучения по закону Стефана- Больцмана. Однако для технических расчетов условно принимают, что суммарная плотность излучения газов, так же как и излучение твердых тел, пропорциональна четвертой степени их абсолютной температуры

(185)

где ε_г – степень черноты газа, ε_г =f(р_i, l, Т).

Приближенные значения средней длины пути луча могут быть найдены из соотношения

(186)

где V – объем газа; F – площадь поверхности его оболочки. Степень черноты газовых смесей определяется как сумма степеней черноты отдельных компонентов.

Плотность теплового потока, передаваемая излучением газами ограждающей поверхности, можно вычислить по приближенной формуле

(187)

где ε_с.г – приведенная степень черноты,

(188)

где ε_г – степень черноты газов; ε_с – степень черноты ограждающей стенки.

Часто в технических устройствах теплота одновременно передается конвекцией и излучением. Тогда суммарная плотность теплового потока q определяется по уравнению

(189)

где T_г, T_c – абсолютная температура газов и стенки, К; α – суммарный коэффициент теплоотдачи конвекцией и излучением, α = α_к + α_л .

Коэффициент теплоотдачи излучением можно определить по формуле

(190)

где T_mа – среднеарифметическая температура, К; Т_mа = 0,5 (Т_г+ T_c).

При теплообмене ограждающей поверхности с капельной жидкостью излучение отсутствует, так как капельные жидкости даже при небольших толщинах слоя непрозрачны и в этом случае α = α_к .