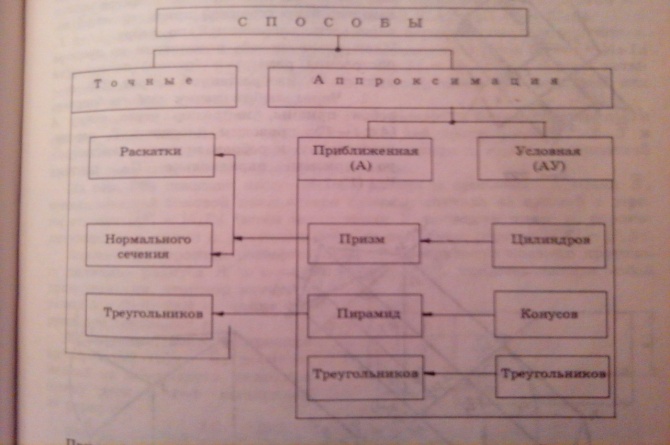
23. Классификация способов построения разверток. Пример построения точной развертки какого-либо геометрического тела.

24. Кратчайшие линии на поверхности. Привести пример построения на эпюре кратчайшей линии, соединяющей две точки какой-либо развертываемой (линейчатой) поверхности.

КРАТЧАЙШАЯ — линия в метрическом пространстве, соединяющая две его точки и не превосходящая по длине любую другую линию с теми же концами.

25. Пересечение геометрических образов. Формулировка алгоритмов №1 и 2. Привести пример использования алгоритма №2 при построении линии пересечения двух плоскостей.

Алгоритм №1: 1.обозначаем на чертеже и обводим соответствующую проекцию искомой линии и точки. Т.е. одна проекция искомой линии (точки) уже дана; 2. Другую проекцию искомой линии (точки) на плоскость проекции П” строим по ее принадлежности второй заданной поверхности (или прямой); 3.определяем видимость проекций: а)найденной линии (точки); б)заданных поверхностей (поверхности и линии; двух тел). Алгоритм №2: 1. Ведем поиск и выбор оптимального посредника Т; 2. Строим посредник Т; 3. Находим линии, по которым посредник Т пересекает каждую заданную поверхность; 4. Отмечаем точки пересечения построенных линий; 5. Операции 1,2,3,4 повторяем нужное число раз; 6. Отмеченные точки соединяем линией в порядке следования образующих любой заданной поверхности; 7. Определяем видимость (если требуется).

26. Привести пример определения алгоритма №3 при построении точки пересечения прямой линии с поверхностью.

Алгоритм №3: 1. Ведем поиск и выбор оптимального посредника; 2. Строим посредник (заключаем заданную линию в посредник – вспомогательную плоскость или поверхность); 3. Находим линию пересечения посредника с заданной поверхностью; 3. Отмечаем точки пересечения построенных линий с заданной; 5. Определяем видимость (если требуется).

27. Свойства и примеры построения (на эпюре) линий пересечения соосных поверхностей вращения.

Соосными называют поверхностивращения, оси которых совпадают. Линия пересечения таких поверхностей строится на основании теоремы о пересечении соосных поверхностей вращения: соосные поверхности вращения пересекаются между собой по окружностям.  Необходимо отметить, если оси пересекающихся соосных поверхностей параллельны плоскости проекций, то окружности пересечения проецируются на эту плоскость в отрезки прямых. Эти отрезки равны диаметру окружности пересечения, а их конечные точки определяются пересечением очерковых линий на этом виде. 

28. Теорема Гаспара Монжа- формулировка, эпюры и примеры использования в технике.

Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересечения линий касания. В соответствии с этой теоремой цилиндры одинакового диаметра имеют общую касательную сферу, пересекаются по двум эллипсам.

29. Сфера и тор. Условия образования сферы и различных видов тора. Определители этих поверхностей; эпюры этих поверхностей.

Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности.