5.5. Цифроаналогові і аналого-цифрові перетворювачі

5.5.1. Цифроаналогові перетворювачі

Розглянуті раніше технічні засоби працюють і з ана-логовыми, і з дискретними параметрами і сигналами. Ядро ав-томатических систем — ЕОМ — працює тільки з цифровими кодами. Для об'єднання усіх цих засобів і вирішуваних ними завдань у рамках єдиної системи треба мати можливість взаємного перетворення величин. Цю задачу вирішують цифроаналогові і аналого-цифрові перетворювачі.

Цифроаналоговий перетворювач (ЦАП) — цей пристрій, який перетворить цифровий код в аналогову величину, соот-ветствующую десятковому числу — еквіваленту цього коду.

Зазвичай вихідною величиной ЦАП є електрична напруга.

Робота цифроаналогового перетворювача заснована на двом ний системі числення. У двійковій системі числення тільки дні цифри — 0 і 1, але вона, як і десяткова система, являється пози ционной, тобто «вага» кожної цифри в числі залежить від її позиції (розряду числа). У десятковій системі кожен більше старший раз ряд «важить» в 10 разів більше за попередній. Так, в числі 555 левМ п'ятірка (2-й розряд) «важить» в 10 разів більше, ніж середня (I I розряд), яка, у свою чергу, в 10 разів «важче» за праву (0-й розряд). Це число можна записати наступним обра-зом:

55510 = 5-102 + 5-101 + 5-10°.

У двійковій системі числення розряди відрізняються в 2 вражаючи в числі 111 (один-один-один) ліва одиниця (2-й розряд) в 2 рази «важче» за середню (1-й розряд), яка в 2 рази «важче» за праву (0-й розряд). Це число можна записати наступним обра-зом:

Враховуючи «ваги» розрядів, можна перетворювати числа з однієї системи числення в іншу, наприклад:

Цей принцип лежить в основі роботи цифроаналогового пре-образователя : будь-яке число в позиційній системі числення можна представити у вигляді суми творів цифр на основа-ние системи числення в мірі, рівній номеру позиції цієї цифри в числі (т. е. номеру розряду).

Для реалізації ЦАП необхідно вибрати «одиницю ваги», наприклад, значення напруги або струму, що відповідає «вазі» самого молодшого розряду числа. Потім в кожному розряді числа, де є цифра 1, ця «одиниця ваги» множиться на «вагу» цього розряду, після чого напруга або струми усіх розрядів складаються. Наприклад, для представленого раніше двійкового числа 10110101 при вибраній в якості «одиниці ваги» силі струму 1 мА підсумкова сила струму, що відповідає цьому числу, опре-деляется таким чином:

При вибраній одиниці молодшого розряду 1мА результатом перетворення двійкового числа 10110101 в аналогову величину — силу струму — являється струм силою 181 мА.

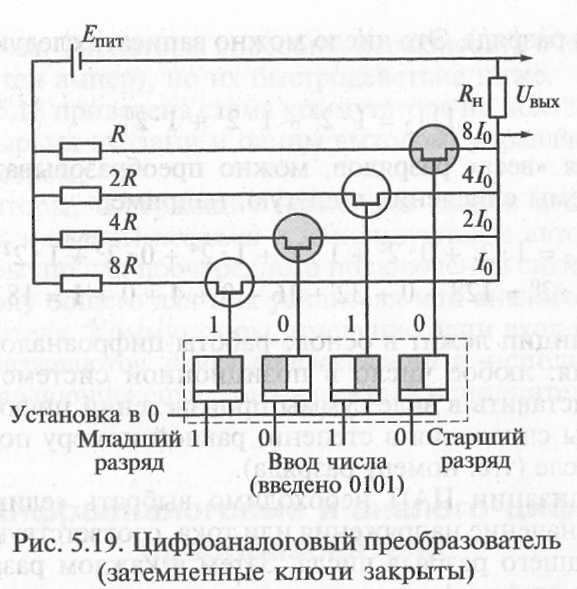
На мал. 5.19 представлена схема 4-розрядного цифроаналогово-го перетворювача, в якій «вага» кожного розряду определяет-ся вибором опору Я ланцюгу, що живиться від джерела з на-пряжением Епт. Управління струмом /в кожному ланцюзі робиться за допомогою паралельного регістра. Підбір опорів рези-сторов виконаний так, що струм, що включається кожним більше стар-шим розрядом, удвічі більше попереднього. Усі струми суммируют-ся на опорі навантаження Кн. Напруга на нім, рівна твору Кн на суму струмів усіх включених розрядів, яв-ииется вихідний величиною 11ъьш перетворювача.

В даному випадку на вхід ЦАП подано двійкове число 0101.Oткрыты транзистори, через які течуть струми I0 і 4 I0. На навантаженні вони підсумовуються і створюють вихідну напругу, соот-ветствующее струму 5I0 (десятковому числу 5).

Типовий цифроаналоговий перетворювач має 12-розрядний регістр, тобто кількість різних його станів 4096. Напруга живлення перемиканих ланцюгів зазвичай вибирається та-ким, щоб вихідний сигнал перетворювача змінювався від — 5,12 до +5,12 В; погрішність перетворення — близько 1 %, час перетворення двійкового коду в напругу — від одиниць до десят-ков мікросекунд.