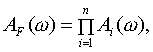- •1. Нелинейные сар. Понятия: «пространство состояний», «фазовая траектория», «фазовый портрет».
- •2. Проблема двойственности в линейном программировании.
- •3. Составляющие информационной системы (ис). Модели жизненного цикла ис.
- •4, 31. Методы определения оптимальных параметров настройки промышленных регуляторов.
- •5. Автоколебания в сар. Определение параметров автоколебаний с помощью графических построений.
- •6,14. Математическая постановка задач оптимального управления. Пример: «Нажимное устройство реверсивного прокатного стана».
- •7,11,59. Назначение, классификация, и функции субд. Структура субд и назначение основных компонентов. Транзакции. Свойства транзакций.
- •8,20. Оценка качества сар по временным характеристикам
- •9. Представление импульсного элемента при исследовании импульсных сар.
- •10. Синтез сар оптимальной по быстродействию.
- •12. Принципы системного подхода в моделировании. Сетевые модели.
- •13. Связь между спектрами сигналов на входе и выходе простейшего импульсного элемента. Теорема Котельникова.
- •15. Модели управления передачей, обработкой и хранением данных в информационных системах на основе технологии «клиент-сервер»
- •16. Непрерывно-стохастические модели на примере систем массового обслуживания.
- •17. Процессы конечной длительности в импульсных сар.
- •18. Метод динамического программирования.
- •19, 55. Характеристика нормальных форм реляционной модели данных.
- •21. Алгебраический аналог критерия устойчивости Гурвица для исар.
- •22. Системы управления на основе нечеткой логики.
- •23. Реляционная модель данных. Понятие функциональной зависимости. Процесс нормализации базы данных.
- •Целостность данных
- •Реляционная алгебра
- •Нормализация базы данных
- •24. Синтез сар по логарифмическим характеристикам.
- •25. Метод гармонической линеаризации нелинейностей.
- •26. Системы управления на основе искусственных нейронных сетей.
- •27,35. Цифровые регуляторы и выбор периода квантования.
- •28. Аппроксимация кривых разгона методом площадей.
- •29. Характер движения в нелинейных и линейных сар.
- •30. Техническая диагностика. Математические основы технической диагностики.
- •32. Функции операционных систем: управление задачами, данными, исключениями и восстановлением.
- •33. Устойчивость линейных сар. Признаки устойчивости. Запасы устойчивости линейных сар.
- •34. Статистические методы распознавания. Метод Бейеса.
- •36.75. Реляционная алгебра Кодда
- •37. Устойчивость линейных непрерывных систем. Критерий устойчивости Найквиста.
- •38. Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент. Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент.
- •Черный ящик
- •39. Определение, назначение и классификация компьютерных сетей. Базовые топологии локальных компьютерных сетей.
- •40. Уровни памяти в вычислительных системах и их взаимодействие. Регистры, кэш, озу, взу. Их типы и классификация.
- •41. Критерий устойчивости Михайлова для непрерывных и линейных сар.
- •Доказательство
- •42. Частотные методы идентификации динамических объектов.
- •43. Определение, назначение и классификация компьютерных сетей. Топология глобальной компьютерной сети.
- •44. Использование внешних устройств в компьютерной сети. Сетевые устройства ввода/вывода,
- •Хранение информации на сервере, файлообменники и внешние ресурсы. Сетевые устройства
- •Типы сетевых устройств Сетевые карты
- •45. Виды корректирующих средств в сар. Недостатки последовательной коррекции.
- •46. Типовые процессы регулирования.
- •Апериодический переходной процесс с минимальным временем регулирования.
- •Переходной процесс с 20%-ным перерегулированием и минимальным временем первого полупериода.
- •Переходной процесс, обеспечивающий минимум интегрального критерия качества.
- •47. Эталонная модель взаимодействия открытых систем osi. Характеристика уровней osi.
- •48. Регистровая память компьютера и её назначение. Типы регистров процессора в реальном режиме. Дополнительные регистры защищённого режима.
- •Новые системные регистры микропроцессоров i80x86
- •49. Гармоническая линеаризация. Физический смысл коэффициентов гармонической линеаризации.
- •50. Идентификация объектов по временным характеристикам. Определение кривой разгона объекта по его импульсной характеристике.
- •51. Общая структура современных асу тп
- •52. Операционные системы потоковой обработки, мультизадачные ос, сетевые ос и ос реального времени. Их особенности.
- •53. Устойчивость нелинейных систем. Метод л.С. Гольдфарба.
- •54. Идентификация динамических систем. Активные и пассивные методы идентификации.
- •Внутренние и внешние, параллельные и последовательные интерфейсы компьютера. Примеры интерфейсов и шин, их основные характеристики.
- •Последовательный и параллельный интерфейсы ввода-вывода
- •57. Точные методы исследования устойчивости и автоколебаний в нелинейных системах. Частотный метод в.М. Попова.
- •58. Методы аппроксимации кривых разгона объекта.
- •61. 65. Статические характеристики нелинейных элементов.
- •62. Обеспечивающие подсистемы информационно - управляющих систем и их характеристики.
- •63. Методы расчета осау. Вариационный метод.
- •Вариационное исчисление
- •64. Назначение системы прерываний эвм. Синхронные и асинхронные, внутренние и внешние прерывания.
- •66. Промышленные регуляторы, их назначение и передаточные функции.
- •67. Функциональные подсистемы информационно- управляющих систем и их характеристики.
- •68. Виртуальные ресурсы в компьютерных сетях. Виртуальные накопители, виртуальные внешние устройства, виртуальная память и виртуальные процессоры.
- •Виртуализация устройств и структура драйвера
- •69. Классификация задач оптимального управления.
- •70. Организационные подсистемы информационно- управляющих систем и их характеристики.
- •71. Методы расчета оптимальных осау. Принцип максимума Понтрягина.
- •Вариационное исчисление
- •Принцип максимума Понтрягина
- •74. Принципы построения автоматизированных систем управления.
- •76. Типы команд и разновидности адресации в микропроцессорах. Cisc, risc и vliw процессоры.
- •Cisc-процессоры
- •Risc-процессоры
- •Vliw-процессоры
- •77. Понятие области нормальных режимов регулятора (онр) и области допустимых настроек регулятора (одн)
- •78. Состав интегрированной системы автоматизации предприятия.
- •79. Математическая модель и математическое моделирование. Этапы математического моделирования.
- •Функционально полные наборы логических элементов
41. Критерий устойчивости Михайлова для непрерывных и линейных сар.
Он был сформулирован
А. В. Михайловым в 1936 году и базируется
на принципе аргумента. При этом для
анализа устойчивости рассматривается
характеристический комплекс системы
F(j![]() )
, который получается из
характеристического полинома
)
, который получается из
характеристического полинома
|
(4.16) |
заменой
p
на
![]() и
имеет вид:
и
имеет вид:
|
(4.17) |
где можно выделить вещественную и мнимую часть, а также амплитуду и фазу:
|
(4.18) |
Для конкретного
численного значения
![]() характеристический
комплекс представляет собой комплексное
число F(j
характеристический
комплекс представляет собой комплексное
число F(j![]() ,
которое
можно изобразить на плоскости в виде
вектора, соединяющего начало координат
с точкой
,
которое
можно изобразить на плоскости в виде
вектора, соединяющего начало координат
с точкой
![]()
При изменении
![]() от
0 до
от
0 до
![]() конец
вектора F(j
)
выписывает
на комплексной плоскости некоторую
кривую, которую называют годографом
Михайлова.
Причем начинается годограф, как следует
из соотношения (4.17), в точке с координатами
{
конец
вектора F(j
)
выписывает
на комплексной плоскости некоторую
кривую, которую называют годографом
Михайлова.
Причем начинается годограф, как следует
из соотношения (4.17), в точке с координатами
{![]() ;
j0}.
;
j0}.

Рис.4.8. Вид годографа Михайлова.
Формулировка критерия. Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении от 0 до начинался на вещественной оси в точке и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в ноль и стремясь к в n-ом квадранте.
Доказательство
Утверждение
основано на расположении годографа
Михайлова на комплексной плоскости,
поэтому проанализируем, как связаны
корни характеристического уравнения
![]() с
видом F(j
).
Поскольку полином (4.16) можно представить
как произведение простых сомножителей
с
видом F(j
).
Поскольку полином (4.16) можно представить
как произведение простых сомножителей
F(p)
= (p -
|
(4.19) |
характеристический комплекс (4.17) также принимает вид:
F(j
)
=
|
(4.20) |
Его можно представить в форме
|
(4.21) |
Из выражений (4.18) и (4.21) следует, что
|
(4.22) |
|
(4.23) |
Если характеристическое
уравнение системы содержит чисто мнимые
корни, то, как следует из (4.22),
![]() при
определенном значении частоты
при
определенном значении частоты
![]() ,
так как при этом один из сомножителей
обратится в ноль. В случае устойчивой
системы корни расположены только в
левой полуплоскости плоскости корней
и не могут быть чисто мнимыми, следовательно,
в ноль годограф Михайлова не обращается.
,
так как при этом один из сомножителей
обратится в ноль. В случае устойчивой
системы корни расположены только в
левой полуплоскости плоскости корней
и не могут быть чисто мнимыми, следовательно,
в ноль годограф Михайлова не обращается.
Определим теперь
угол поворота вектора F(j
)
при изменении частоты от 0 до
.
Поскольку
![]() ,
в соответствии с (4.23), есть сумма отдельных
,
в соответствии с (4.23), есть сумма отдельных
![]() ,
то рассмотрим угол поворота каждого
сомножителя выражения (4.20).
,
то рассмотрим угол поворота каждого
сомножителя выражения (4.20).
Корень
характеристического уравнения
вещественный отрицательный;
![]() Соответствующий
сомножитель в (4.20)
имеет вид: (
Соответствующий
сомножитель в (4.20)
имеет вид: (![]() ).
).
Рис.4.9. Элементарный вектор, соответствующий устойчивому вещественному корню |
Изобразим этот
элементарный вектор на комплексной
плоскости; при изменении
от
0 до
его
вещественная часть остается неизменной
и равна
Как
видим, угол поворота элементарного
вектора, соответствующего устойчивому
вещественному корню, равен
|
Если корень
характеристического уравнения
вещественный положительный,
![]() ,
то угол поворота элементарного вектора
,
то угол поворота элементарного вектора
![]() равен
равен
![]()
Рассмотрим теперь
пару устойчивых комплексно - cопряженных
корней
![]() и
соответствующий им угол поворота
произведения
и
соответствующий им угол поворота
произведения
![]()
Рис.4.10. Векторы, соответствующие устойчивым комплексно - сопряженным корням |
У векторов А, В
начальные фазы одинаковы по модулю
( |
Суммарный угол
поворота для пары устойчивых комплексно
- сопряженных корней равен
![]()
Если комплексно
- сопряженные корни имеют положительную
вещественную часть, то суммарный угол
поворота равен
![]()
Таким образом, в
устойчивой системе каждый из n
корней даст приращение фазы
![]() ,
а общий угол поворота F(j
)
согласно (4.23)
равен
,
а общий угол поворота F(j
)
согласно (4.23)
равен
![]() ,
что и требовалось доказать. Вид годографа
Михайлова для устойчивых и неустойчивых
систем третьего порядка приведен на
рис.4.11.
,
что и требовалось доказать. Вид годографа
Михайлова для устойчивых и неустойчивых
систем третьего порядка приведен на
рис.4.11.

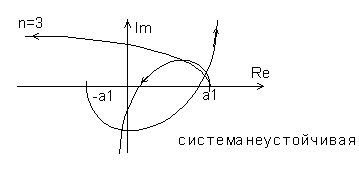
Рис.4.11. Годограф Михайлова для устойчивой и неустойчивой систем
Система будет находиться на границе устойчивости, если годограф Михайлова при некотором значении частоты обращается в ноль, то есть при выполнении условия:
|
(4.24) |
Здесь частота 0 - есть частота незатухающих колебаний системы.
Пример 4.5.
Вид годографа Михайлова неустойчивой системы шестого порядка:

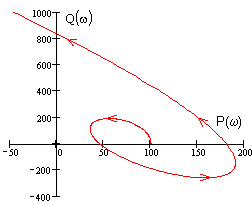
Пример 4.6.
Вид годографа Михайлова системы третьего порядка в зависимости от вличины коэффициента передачи:

|
|
|
Пример 4.7.
Оценить
устойчивость системы, структурная схема
которой имеет вид:

Определим передаточную функцию системы
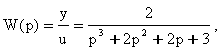
и запишем ее характеристический полином
![]()
Заменой
p на
![]() перейдем
к выражению для годографа Михайлова
перейдем
к выражению для годографа Михайлова
![]()
которое представим в форме
![]()
С целью построения годографа Михайлова вычислим значения вещественной и мнимой части при конкретных значениях частоты и занесем их в таблицу.