§11.Предел функции в точке

1.Основные определения

56. Л юбой интервал, содержащий точку , называется окрестностью точки . Симметричный интервал при любом 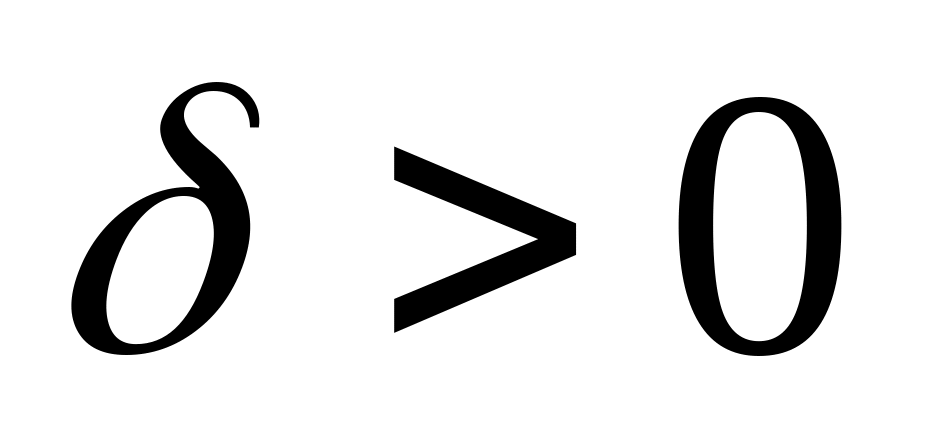называется -окрестностью точки . -окрестность точки можно записать с помощью неравенства: 

В ыколотая -окрестность точки – это множество точек: , или .

Пусть функция определена в некоторой выколотой окрестности точки .

56. Число называется пределом функции при , стремящимся к (или в точке ), если для любого положительного числа найдётся такое положительное число , что при всех , удовлетворяющих неравенству , будет выполняться неравенство 

Обозначение: .

С помощью кванторов это определение запишем так:

Если число является пределом функции в точке , то геометрически это означает, что график функции для находится внутри прямоугольника, ограниченного прямыми ; ; ; .

О днако точка (если в точке функция определена) может как принадлежать, так и не принадлежать этому прямоугольнику (рис. 29).

Если число устремить к нулю, то этот прямоугольник будет стягиваться к точке , и, значит, когда точка стремится к точке , то точка графика функции стремится к точке .

64. Докажите, что .

Функция определена в любой окрестности точки . Неравенства , , будут выполняться для всех , удовлетворяющих условию . Таким образом, , это и означает, что .

Не для всякой функции, определённой в окрестности точки , существует предел при . Например, функция

Э та функция (рис. 30) не имеет предела в точке . (Докажите самостоятельно).

2.Односторонние пределы

56. Правой окрестностью точки а называется любой интервал .

Пусть функция определена в некоторой правой окрестности точки .

56. Число называется пределом справа функции в точке , если для любого положительного числа найдётся такое положительное число , что для всех , удовлетворяющих условию , выполняется неравенство . При этом пишут: . Часто вместо пишут .

То есть .

Аналогично определяется предел слева.

56. Левой окрестностью точки называется любой интервал .

Пусть функция определена в некоторой левой окрестности точки .

56. Число называется пределом слева функции , если для любого положительного числа найдётся такое положительное число , что при всех , удовлетворяющих условию , выполняется неравенство  При этом пишут: или .

То есть .

Наглядное представление об односторонних пределах дает:

64. Пусть - объем 1кг при температуре . Тогда - объем 1кг льда при температуре , а объем 1кг жидкой воды при той же температуре. Из курса физики известно, что (это обстоятельство приводит, например, к тому, что при замерзании воды в водопроводных трубах они лопаются).

13. (необходимое и достаточное условие существования предела функции в точке). Для того, чтобы число было пределом функции в точке, необходимо и достаточно, чтобы существовали оба односторонних предела и и они были равны между собой: .

Докажите эту теорему самостоятельно.

64. Пусть . Найдем односторонние пределы этой функции в точке .

, тогда ; ;

, тогда ; .

Итак, .