Глава 4.Предел и непрерывность функций §10.Предел функции на бесконечности

1.Основные определения

Аналогично определению предела последовательности введём определение предела функции на бесконечности.

Известно, что .

Пусть функция определена в окрестности бесконечности (то есть, определена вне некоторого отрезка , где ).

56. Число называется пределом функции при , стремящемся к бесконечности, если для любого положительного числа найдётся такое положительное число , что для всех , удовлетворяющих условию , выполняется неравенство .

Обозначается: .

С использованием кванторов определение записывается так:

64. Доказать, что .

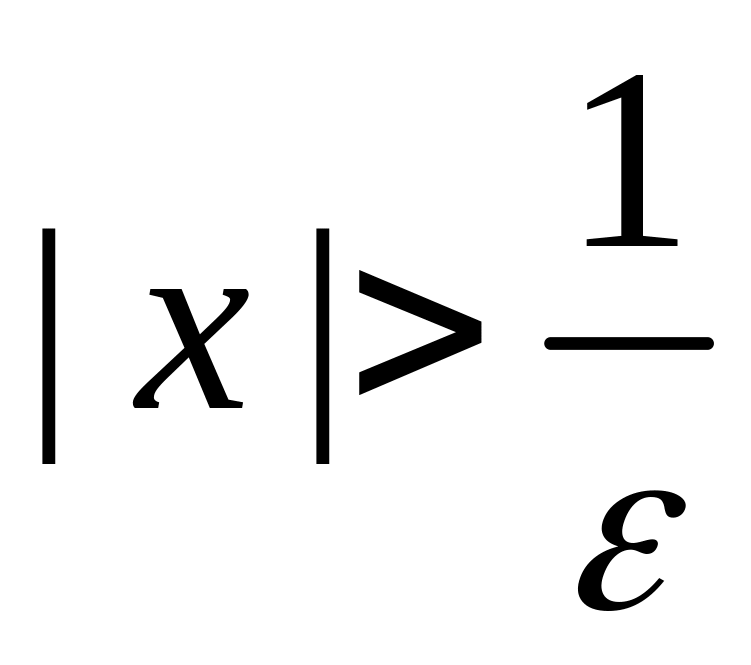
1. Функция определена для всех . Для любого неравенство или будет выполняться, если  Таким образом

Это и означает, что .

Часто различают существование пределов функции отдельно при и .

56. ( См. рис. 24)

56. ( См. рис. 25)

56. ( См. рис. 26). Для того, чтобы существовал предел функции на бесконечности, необходимо и достаточно, чтобы .

2.Бесконечно малые функции и их свойства

56. Функция называется бесконечно малой при , если

64. – бесконечно мала при и , так как .

Свойство бесконечно малых функций

13. Если функции и бесконечно малы при , то сумма бесконечно мала при .

2. Так как и – бесконечно малые при , то найдутся лучи и , на которых для любого соответственно выполняются неравенства и . На общей части этих лучей выполняются оба неравенства, следовательно,  Таким образом, для любого существует луч, на котором , значит, – бесконечно малая при 

Следствие 1. Если функции бесконечно малы при , то функция – бесконечно мала при .

13. Произведение ограниченной функции на бесконечно малую – бесконечно малая функция.

3. Пусть – ограниченная, а – бесконечно малая при значит, и

.

Рассмотрим модуль произведения для всех , принадлежащих общей части лучей и . Пусть . Итак, , а это значит, что - бесконечно малая при .

Следствие 2. Произведение конечного числа бесконечно малых – бесконечно малая при 

Примечание: Теорема 13 и 14 сформулированы и доказаны при . Аналогично формулируются соответствующие теоремы при и .

13. Для того, чтобы функция имела при предел, равный , необходимо и достаточно, чтобы выполнялось соотношение , где – бесконечно малая при .

4. 1) (необходимость)

Пусть , значит, обозначим , тогда , где – бесконечно малая, так как .

2) (достаточность)

Пусть , где – бесконечно малая при , тогда , но , значит, , таким образом, .

Рассмотрим несколько примеров.

64. Докажите, что 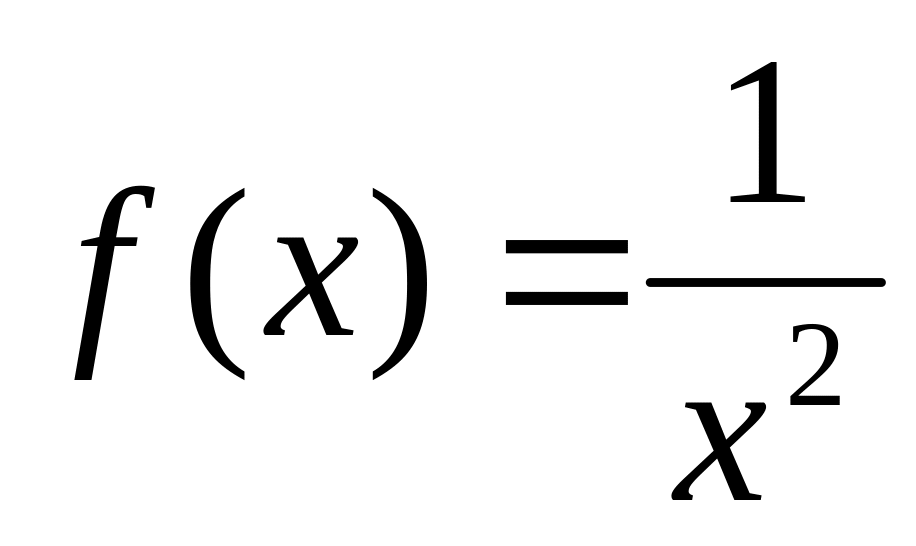бесконечно малая при .

5. , значит, - произведение функций бесконечно малых при , следовательно, бесконечно малая при .

Докажите самостоятельно, что для любого функция бесконечно малая при .

64. Докажите, что , бесконечно малая при .

6. Так как 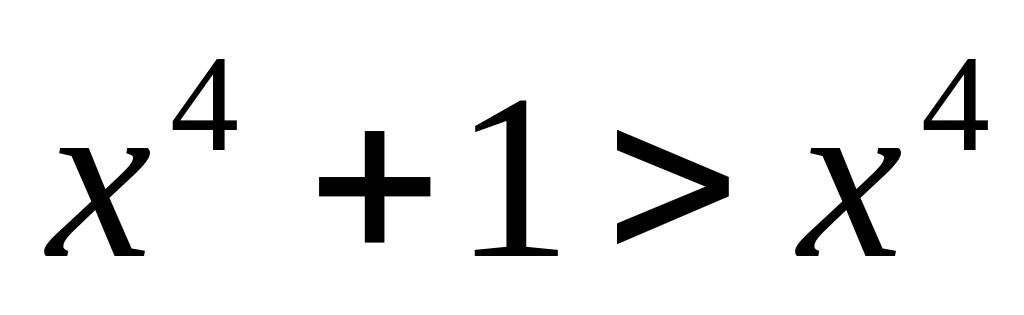, то при , - бесконечно малая при , значит, , бесконечно малая при .

64. Докажите, что .

7. рассмотрим , функция бесконечно малая при , бесконечно мала и функция при , значит, .