27 Множення матриць

Добутк матриці А (розмірів mхk) на матр В (kхn) називається М С=АВ розмірів m на n, елементи якої дорівнюють сумі добутків відповідних елементів і-го рядка А і j-го стовпця В. {AB}_ij=∑^k_s=1a_is*b_sj (1)

Множ матр можливе лише тоді, коли к-сть стовбців А = к-сті рядків В.

Властивості добутку матриць

1) α(АВ)=( αА)В=А(αВ)

2) (А+В)С=АС+ВС

3) А(В+С)=АВ+АС

4) (АВ)С=А(ВС)

5) (АВ)^т=В^тА^т

Доведення

Властивості 1-3 очевидні

{(AB)C}_ij A m*n, B p*k, C k*n

{(AB)C}_ij=∑^k_l=1 (∑^p_s=1a_isb_sl)c_lj

{(AB)C}_ij=∑^p_s=1a_is(∑^k_l=1b_sl c_lj) Одерж суми відрізн лише порядком доданків. Отже маємо рівність відпов ел

{(AB)^т}_ij={AB}_ij=∑^k_s=1a_jsb_si=∑^k_s=1{A^т}_sj{B^т}_is=∑^k_s=1{B^т}_is{A^т}_sj={B^т A^т }_ij

У загал випадку АВ≠ВА навіть можливо, що ВА – не існує .

Введемо поняття лінійної комбінації стовбців і рядків А. Позначимо і-тий рядок А а_і.=(а_і1,a_i2,...,a_in) a._j=(a_1j,a_2j,...,a_mj)^т

Лін комбінацією рядків матриці А називається сума ∑^m_i=1α_ia_i. , де α_i – дійсні, і=1,m

Лін комбінацією стовбців матриці А називається сума ∑ⁿ_j=1 β_ja._j , де β_j є R, j=1,n

Перепишемо формулу (1) у 2 випадках

{AB}._j=∑^k_s=1a._sb_sj (2) {AB}_i.=∑^k_s=1a_isb_s. (3)

Ф-ла (2) показує, що будь-який j-тий стовбець є лінійною комбінацією стовбців А при чому коефіцієнти утворюють j-тий стовбець В.

З (3) випливає, що і-тий рядок В є лінійною комбінацією рядків В. Коефіцієнти лінійної комбінації є елементами і-того рядка А. Отже, якщо треба працювати зі стовбцями (рядками) матриці то треба помножувати матрицю на відповідні матриці справа(зліва).

28 Елементарні перетворення матриць

Елементарними називаються такі перетворення:

1. множення рядка (стовпця) на число, що не дорівнює 0;

2. дод до рядка(ст) іншого рядка (ст), помноженого на довільне число

3. переставлення будь-яких рядків(стовпців)

Дві матриці називаються еквівалентними, якщо кожна з них отримується з іншої за допомогою скінченої кількості елементарних перетворень. Якщо елементарні перетворення застосовуються до одиничної матриці Е то одержимо матрицю, яка є елементарною. Введемо позначення елементарних матриць:

Е_і(λ) – множення і-того рядка на число λ .

Е_ij(λ) – додавання і-того рядка j-того рядка, помноженого на λ.

Е_ij – переставлення і-того і j-того рядків Е.

З (3) випливає, що кожне елементарне перетворення з рядками В рівносильне множенню її зліва на відповідну елементарну матрицю.

З (2) випливає, що елементарні перетворення стовбців А рівносильні множенню її справа на елементарні матриці.

Е_і^т(λ)=Е_і(λ) Е_ij^т=Е_ij

29. Обернена матриця.

Матриця А^-1назив оберненою до квадр матр А, якщо виконується А^-1*А=А* А^-1=Е

Теорема1. Якщо матриця А – не вироджена, то існує обернена до неї і обчисл. За формулою

d et А не=0

А11 А21 … Аn1

A12 A22 … An2

А^-1=1/ det А* ………………………. Де Aij – алгебр

………………………. доповнення

A1nA2n … Ann елем аij

Доведення: (за озн) АА^-1–матриці n-го порядку

Узагальнена формула Ла-Пласа

Властивості:

1)Якщо А^-1 існує, то вона єдина.

Дов. Від супротивного. Нехай існує матриця В така, що АВ=Е: А^-1=А^-1Е=(А^-1А)В=ЕВ=В; А^-1=В

З іншого боку, нехай існує С така, що СА=Е

А^-1=Е А^-1=С(АА^-1)=СЕ=С; А^-1=С

2)(А^т)^-1=(А^-1)^т

Дов. (АА^-1)^т=(Е)^т

(А^-1)^т * А^т=Е =>Якщо А – невиродж (існ А^-1), то А^-т - невиродж і існує (А^т)^-1; в силу оберненості матр (А^-1)^т=(А^т)^-1

3)(АВ) ^-1=В^-1 * А^-1

Дов. За озн. (АВ)(АВ)^-1=Е?

А(ВВ^-1)А^-1=АЕА^-1=АА^-1=Е; (АВ)^-1=В^-1А^-1

Теорема2.Будь-яку не вироджену матр можна предст-ти у вигляді добутку елементарних матр.

НехdetA не=0. Нех а₁₁ не=0. Поділимо перший рядок на а₁₁. Тобто матр А множ зліва на елементарну Е1(а₁₁^-1). Далі множимо перший рядок на –а_і1 і додаємо до і-го рядка посл. Одержимо: Е_n1(-а_n1)…Е₃₁(-а₃₁)Е₂₁(-а₂₁)Е₁₁(а₁₁^-1)А=

1 a`<sub>12</sub> … a`_1n

= 0 a`<sub>22</sub> … a`_2n

……………

0 a`<sub>n2</sub> … a`_nn

Зауваж. У випадку а₁₁=0 шукаємо елем а_j1 не=0 та переставл на 1 місце. Продовжуюяи процес множення зліва на елем-ні матр зведемо початкматр до один-ої.

lA=E; l – добуток елементарнматр

l – не вироджена, бо утвор в результневиродж перетворень. При цьому:

d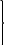 etE_i(β)=β не=0 E_i(β)=E(β^-1)

detE_ij(β)=1 E^-1_ij(β)=E(-β)

detE_ij=-1 E^-1_ij=E_ij

l^-1– існує, l^-1–добуток обернених матриць до елементарн матриць. Але обернені до елем-них є елемен-ми. l^-1=А.

Наслідок: зі співвідношення lА=Е випливає А ^-1= l

Теорема. Якщо хоча б одна з матриць А або В – невиродж, то виконується: det(АВ)=(detА)*(detВ)

Дов.Нех А не=0 = за теоремою2 її можна представ у вигляді добутку елементарних матр. Досить перевір, що твердж вірне для елементарних матриць:

1.det(Е_i(β)В)= βdetB(за змістомвизначника)= =detЕ_i(β)*detВ;2.det(Е_ij(β)В)=1*detВ=detЕ_ij(β)*detВ;

3.det(Е_ijВ)=-1*detВ=detЕ_ij*detВ; доведено.

Властивості:4-5 Якщо матрА–невиродж, то det(А^-1)= =(detА^-1); (А^-1) ^-1=А

Дов. АА^-1=Е; det(АА^-1)=detЕ; detА*det(А^-1)=detЕ=1;

det(А^-1)=(detА)^-1;

A^-1 – не вироджена за власт 4. Тоді існ (А^-1)^-1. Тоді:

(АА^-1)^-1=Е^-1; (А^-1)^-1А^-1=Е, але АА^-1=Е; (А^-1)^-1=А – в силу єдиностіобернматр.