15. Векторне і нормальне рівняння площини

Обираємо в сист. координат т.Р; радіус-вектор ОР=р; складемо р-ня площини, що проходить через т.Р ┴OP. Рє(π), р┴(π). Візьмемо т.М, Мє(π)-поточна точка. r=OM – радіус-вектор т.М. РМ=r-р; РМ┴р; ↔РМ*р=0; (r-p)p=0(1)- векторне р-ня площини. Перейдемо в р-ні(1) до координатної форми р=│р│*е_р; │р│=р>0; е_р=n – орт нормалі до площини. n=(cosα;cosβ;cosγ); M(x;y;z); r=(x;y;z); p_=pn_

p(cosα;cosβ;cosγ)*(x- cosα; y-cosβ; z-cosγ)=0;

xcosα+ycosβ+zcosγ-pcos²α-pcos²β-pcos²γ=0;

xcosα+ycosβ+zcosγ-p*1=0;

p= xcosα+ycosβ+zcosγ (2) – нормальне р-ня площини, де n=(cosα;cosβ;cosγ)-орт нормалі до площини, р- відстань площини від початку координат.

16. Загальне рівняння площини.

Загальним р-ням площини в R₃ назив. лінійне р-ня вигляду:

(3) Ax+By+Cz+D=0, де A,B,C,DєR, A²+B²+C^2≠0. Покажемо, що р-ня (3) можна звести до p= xcosα+ycosβ+zcosγ(2) і навп. Домножимо (2)на р:

(2) ↔ xрcosα+yрcosβ+zрcosγ-p²=0. Познач A=рcosα, B=рcosβ, C=рcosγ, D=-p² Отже отримуємо р-ня(3), де N=(A;B;C)-вектор нормалі до площ π.

Для того, щоб (3)звести до(2),домнож (3) на нормувальний множник μ

μAx+ μBy+ μCz+μD=0 μ визнач з умов:μA=cosα,μB=cosβ,μC=cosγ, Dμ<0.

звідки μ²(А²+В²+С²)=1;→ μ=±1/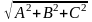 (знак вибир протилеж знаку D) Отже, маємо р-ня площ у вигл: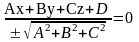 , яке і є р-ням(2).

В исновок: будь-яке лін р-ня вигляду (3) можна звести до р-ня (2), яке є норм р-ням площ, і навпаки, якщо в пр R₃ задана довіл площ і фіксов довільна декартова сист. коорд Охуz, то площ визначається в цій с-мі лінійним р-ням.Відстань та відхилення від площини.

z

M

P

M₀

p

y

opt n

x

Нехай задана площина(π) і т., що не лежить на цій площині.

(π): xcosα+ycosβ+zcosγ-p=0; М₀(x₀;y₀;z₀) не є(π). Спроектуємо ОМ₀ на вісь, задану n(OP).

OM= пр _nОМ₀=OM₀n;

Відхиленням т. М₀ від (π) назив. різниця проекцій:

δ= пр _nОМ_0; - пр _nOP;

Отже, маємо:δ= xcosα+ycosβ+zcosγ-p або

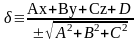
δ=0 - М₀є(π); δ>0 – М₀ і О по різні боки від (π); δ <0 – по один бік.

Відстань точки від площини:

d=│ δ │=│ xcosα+ycosβ+zcosγ-p│=│ │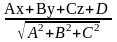

Чачтинні випадки загального р-ня:

1) D=0 – площина прох. через початок координат( через т.(0;0;0))

2)А=0, В,С≠0, Ву+Сz+D=0 –площ. паралельна Ох.

3)А=В=0, Сz+D=0 – площ. паралельна Оху і т.д.

17. Кут між двома площинами.

Нехай дано дві площини, які визначаються загальними рівняннями:

A_1x+B_1y+C_1z+D₁=0 , A_2x+B_2y+C_2z+D₂=0

Розглянемо вектори нормалей до кожної з площин:

N₁= 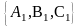, N= .

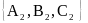(1)Кут φ між площинами визначаеться кутом φ між векторами N₁ i N₂ . Отже, справджується рівність:

Cosφ=(A₁A₂+B₁B₂+C₁C₂) / ( 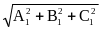* 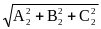)=N1N2/|N1||N2|

(2)Умова перпендикулярності площин така:

A₁A₂+B₁B₂+C₁C₂=0

(3)Умова паралельності площин:

A₁/A₂=B₁/B₂=C₁/C₂

(4)Дві площини збігаються, якщо виконується рівність:

A₁/A₂=B₁/B₂=С₁/С₂=D₁/D₂

У разі виконання умови (4) рівняння однієї площини можна дістати з рівняння іншої площини множенням на сталий множник.

Нехай дано три площини:

A_kx+B_ky+C_kz+D_k=0 (k=1,2,3)

Вони перетинаються в одній точці у тому і тільки у тому разі, коли:

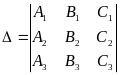не=0

Якщо визначник дорівнює нулю, то площини можуть мати спільну пряму, коли система рівнянь має нескінченну множину розв’язків, або не мати жодної спільної точки, коли система не має розв’язків.

18. Пряма на площині.Кут між прямими

А)

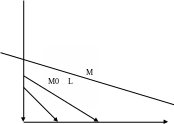
Векторне рівняння прямої на площині

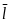- напрямний вектор прямої L; t-параметр

М₀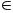 L , M L , ||L , OM₀=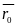 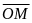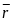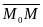_, = , || , =t* , = - ,

t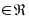 , = + t* (1), -векторне р-ня прямої що прох через т. радіус-вектор якої ,паралельно вектору .

Параметричне рівняння прямої

М₀(х₀,у₀), =(m,n), M(x,y), r(x,y). P (1):

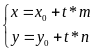t є R(2)

Канонічне рівняння прямої

З (2): t=(x-x₀)/m; t=(y-y₀)/n

(x-x₀)/m=(y-y₀)/n (3) канон р-ня прямої, що прох через т з коорд(х₀, у_о), паралельно напрямному відрізку l з коорд(m,n)

m²+n²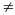 0

якщо m=0

(x-x₀)*n=0 =>x=x₀ – пряма, парал осі Оу

Рівняння прямої що проходить через 2 задані точки

P

P₁

P₂

P

₁(х₁,у)

P ₂(х₂,у₂)

P (х,у)

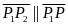
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)(4)

Рівняння прямої з кутовим коефіцієнтом

Візьмемо (3) і розв’яжемо відносно у. y=(n/m)x+(y₀-(n/m)x₀)→

y=kx+b(5)

З

L

агальне рівняння прямої

С кладемо р-ня прямої, що прох через т.Р₀(x₀,y₀)

перпендик до вектора 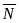(A,B). Р-поточ точка

L 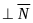; Р₀єL ; Р(x,y) , 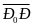* =0

A

l

(x-x₀)+B(y-y₀)=0

A

n

x+By-Ax₀-By₀=0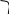

(

φ

-Ax₀-By₀)=C

A

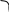
m

x+By+C=0(5)

Кути!

Розглянемо дві прямі, які задано рівняннями з кутовими коеф:

y = k₁x + b₁ , y = k₁x + b₁ (1).

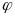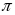якщо прямі паралел, то вони мають однак кути нахилу;дві прямі збіг, якщо: k₁ = k₂ , b₁ = b_{2 ;} якщо прямі взаємно перпендик, то: ₁= ₂+ /2 i

k₂=tg ₂=tg( ₁+ /2)=-ctg ₁=-1/tg ₁=-1/k₁ рівність: k₂=-1/k₁ є умовою перпендикул двох прямих.

якщо прямі не парал, то вони перетин в точці , коорд якої є розв’язком системи рівнянь:

y=k₁x+b,

y=k₂x+b₂

нехай - кут між цими прямими : (рис.1)

згідно з рис.1 маємо: ₂ = ₂ + 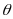(зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів,не суміжних з ним). Отже,

tg =tg( ₂- ₁)=(tg ₂ – tg ₁)/(1+tg ₂*tg ₂)=(k₂-k₁)/(1+k₂k₁)

формулу:

tg =(k₂-k₁)/(1+k₂k₁) застосов для знаходж кута між 2 прямими, заданими рівняннями виду (1).

19. ПРЯМА В ПРОСТОРІ

1.) Векторне р-ня

r=r₀+tl, де r-радіус-вектор змінної точки P, r₀-радіус вектор заданої точки М₀, l- ненульовий напрямний вектор t-параметр. tЄR

2.)Параметричні р-ня

l =(m,n,p) r₀=(x₀,y₀,z₀)

x =x₀+tm

y=y₀+tn параметричне рівняння

z=z₀+tp

3) (x-x₀) = (y-y₀) = (z-z₀) канонічне рівняння

m n p

4) Рівняння прямої через дві задані точки

P₁(x₁,y₁,z₁) P₂(x₂, y₂, z₂)

(x-x1) = (y-y1) = (z-z1)

x2-x1 y2-y1 z2-z1

5) Загальне рівняння прямої

Пряма задається за допомогою перетину двох площин

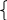A1x+B1y+C1z+D1=0 де

A2x+B2y+C2z+D2=0

Зауваження: Для зведення з загального рівняння прямої до канонічного:

1.Знайдемо т.Р₀, що належить L. Наприклад, z=0, шукаємо х,у з с-ми якщо визначник А1 В1 не=0. Якщо ж =0, шукаємо інший варіант.

А2 В2

2.Напрямний l || N1xN2, де N1, N2– нормалі. N1(A1,B1,C1) N2(A2,B2,C2)

20. Кут між пр в прост. Умови належн двох прямих одній площині

Кут між пр. в простор визнач як кут між їх напрямними векторами

Нехай прямі л1 та л2 задано рівняннями:

(x-x1) = (y-y1) = (z-z1) (x-x2) = (y-y2) = (z-z2)

m1 n1 p1 m2 n2 p2

Кут між цими прямими дорівнює куту β між її напрямними векторами l1=(m1,n1,p1) l2=(m2,n2,p2) тому дістанемо.

Умова || прямих: L1 || L2 ↔ m1/m2=n1/n2=p1/p2

Умова ┴ прямих: L1┴L2 ↔ m1m2+n1n2+p1p2=0

Кут між цими прямими дорівнює куту β між її напрямними векторами l1=(m1,n1,p1) l2=(m2,n2,p2) тому дістанемо:

Соs β =l1*l2 = m1*m2 +n1*n2+p1*p2 ________

|l1|*|l2| √ (m1*m1+n1*n1+p1*p1) * √((m2*m2+n2*n2+p2*p2)

З'ясуємо коли 2 прямі лежать точно в 1 площ:

Якщо l1, l2, P1P2 лежать в 1 площ, то 2 прямі-в 1 площ. З цього виплив, що їх мішаний добуток=0

P1P2: х2-х1 у2-у1 z2-z1

l1 : m1 n1 p1 =0

l2 : m2 n2 p2