11 Декартова система координат

Розглянемо в-ри в просторі R3 , ортоном базис , . В-ри попарно ортогон . Зведемо ці в-ри до спіл поч 0 та розташ їх так, щоб утвор праву трійку.Візьмемо будь-як вектор і відклад від т. О.Провед через т.А площини ІІ до Ох, Оу, Оz. Одержимо точки при перет з осями визнач числ пр на осі коорд. 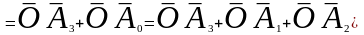. = 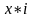, = , = . X= , y= ,z= Отже, маємо розклад за ортами дек прямок с-ми коорд. =хі+yj+zk=(x,y,z)

Введ кути між і ос коор: , , З власт 2 пр маємо: cos = ; cosb= ; cosj= (за означ. cos) За теор. Піф з мал. маємо: . cos Ці cos кутів є коорд. орта: Переформ в коорд. формі означ та лін. опер над вект:1) =(0;0;0) 2) = , =(x1;y1;z1), (x2;y2;z2)=>x1=x2, y1=y2,z1=z2; 3) =( x; y; z). 4) +- =(x1+-x2;y1+-y2;z1+-z2)

4) = , A(x1,y1,z1), B(x2;y2;z2); =(x2-x1;y2-y1;z2-z1)

12Скалярний добуток векторів

скалярним добутком векторів а і b називається число аb, яке дорівнює добутку модулів цих векторів на косинус кута між ними.

Зауваження:1)Скал квадрат: а²=а*а=|а|², 2)cosφ=ab/|a||b|

Властивості:

1. а*b = |a|_пр.а* b = |b|_пр.b * a

2. ai=пр_ia=пр_oxa=x висн: координата вектора в декарт с-мі корд є скаляр добут вектора на відповід орт декарт с-ми корд.

3. а*b = b*а

4. (a)*b =  * (ab)

5. a(b+c) = a*b + a*c

6. a*b = 0 <=> a = 0  b = 0  ab

Ознака ортогональності: два ненульові вектори ортогональні тоді і тільки тоді, коли їх скалярний добуток дорівнює 0.

Координатна форма скалярного добутку:

Нехай задано a і b в координатній формі.

a = x₁*i + y₁*j + z₁*k

b = x₂*i + y₂*j + z₂*k

ab=(x₂*i + y₂*j + z₂*k)( x₁*i + y₁*j + z₁*k) = x_1*x₂ + y_1* y₂ + z_1* z₂

Наслідок:a²=|a|²=x1²+y1²+z1²

cos =

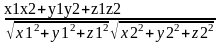
13Векторний добуток векторів

Вект доб а і b наз вектор с=ахb=[a,b] такий, що 1)|c|=S_nap-площа парал, побуд на векторах a i b. 2) c┴a, c┴b(c┴площ,в якій леж а і b) 3)a,b,c утвор праву трійку.

Властивості:

1. |axb|=|a|x|b|sinφ, φ=(a кут b)

2. axb=-bxa

3. (λa)xb=λ(axb)=ax(λb)

4. (a+b)xc=axc+bxc

5. axb=0↔(a=0)v(b=0)v(a||b)

Координатна форма:

Нехай a=x1i+y1j+z1k b=x2i+y2j+z2k

axb=(x1i+y1j+z1k)x(x2i+y2j+z2k)=x1x2ii+x1y2ij+x1z2ik+y1x2ji+y1y2jj+y1z2jk+z1x2ki+z1y2kj+z1z2kk=x1y2k-x1z2j-y1x2k+y1z2i+z1x2j-z1y2i=

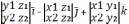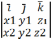= = axb.

Площа парал і трик в R3 i R2:

Паралелогр утвор векторами а і b. Тоді S_nap=|axb| - модуль вектора

S_тр=1/2|axb|

Якщо в-ри задані корд кінців a=AB, b=AC

A(x1,y1,z1); B(x2,y2,z2); C(x3,y3,z3)

S_nap=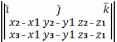 , S_тр=1/2…

R2:

z1=z2=z3=0…..те саме без z

14. Мішаний добуток трьох векторів.

Мішаним (векторноскалярним) добутком векторів 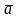, , 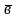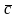.назив. число вигляду

=( )

Властивості мішаного добутку

1) ( ) = ( )= ( )= ( )

2) =0 =0 або =0 або =0 або , , - компланарні

3) Модуль мішаного добутку векторів дорівнює об'єму паралелепіпеда побудованого на цих векторах.

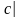=Vпар.

= |( ) |=axb |np_axbc|=V

| |=Sпар. Звідси h=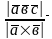

Об'єм тетраедра побуд.на , ,

Vтетр.=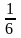

ознака компланарності 3 векторів

три ненульові вектори компланарні тоді і тільки тоді, коли їх добуток дорівнює нулю.

Координатна форма мішаного добутку

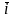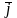=(x₁ +y₁ +z₁ )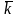

=(x₂ +y₂ +z₂ )

=(x₃ +y₃ +z₃ )

x₁ y₁ z₁

=( ) = x₂ y₂ z₂

x₃ y₃ z₃