66) Зчисленна потужність

Озн: Множина – рівнопотужна N називається зчисленною множиною , а потужність (N) – зчисленна потужність

Властивості зчисленних множин

Т: будь-яка нескінченна множина містить зчисленну підмножину.

Доведення: Нехай Х –нескінченна множина, тоді х1 Х

Розглянемо множину Х\{x1} 0 …. х2 Х\{x1}, …..,хn є Х\{x1,...,xn-1} продовжуючи цей процес , побудуємо множину {x1,x2,…,xn,…} X

T: Будь-яка нескінченна підмножина зчисленної множини – зчисленна.

T: Якщо кожна з множин x1,x2,…,xn,… не більше ніж зчисленна ( скінченна або зчисленна), то об’єднання цих множин, теж не більше ніж зчисленна.

Теорема: Множина всіх раціональних чисел - зчисленна

Доведення: Випишемо всі раціональні числа, подавши їх у вигляді таблиці, що має нескінченну кількість рядків і стовбців.

В кожному n-му рядку роз-ні раціональні нескоротні дроби із знаменником n

Після впорядкування: Q~N

Теорема: будь- який відрізок множини дійсних чисел складається з несчисленної множини точок.

67) Континуальна потужність

Теорема: будь який відрізок множини дійсних чисел скл з незчисленої множини точок. Зауваж: [a,b]~[c,d]~[0,1]

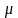([0;1]) – континуальна потужність

R~(0;1)~[0,1].Отже (R)= ([0,1]);( (R)-конт пот-ть)

Доведення (відсупрот): [a,b] , a<b , a,b RПрипустимо ,щовідрізок – счисленнамножина

[a,b]={x1,x2,…,xn,…}; [a1,b1] [a,b]; x1 не [a1,b1] x1 не [a2,b2] [a1,b1] [a,b]

Одержимо систему вкладенихвідрізків [an,bn] [a,b] , вони не містятьточокx1,x2,…,xn .Отжежодна точка хn, n N не буде належатипрерізувкладенихвідрізків.

Зіншого боку вкладенівідрізкимають:

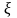[an,b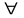n] n N; [a,b] => n0 N

=xn0 =>xn0= [an0,bn0] -суперечність по будовівкладенихвідрізків. Висновок:відрізок АВ – несчислен.

[0,1]˜R => (R)= ([0,1])

Дов. 1.Дов, що R-несчисл(від супрот)

НехR–счисл.[0,1]cR =>[0,1]-cчисл,що супереч умові.

R-несчислена.

2.(0,1) c [0,1] cR; (0,1)<= ([0,1])<= (R);

(0,1) ˜R => (0,1)= (R); то (R)= ([0,1])

Гіпотеза Кантора: Не існуєпотужностібільшої за счисленну і меншої за континуальну. Не існує потужності максимальної.