55) Означення функції. Види відображень.

Відображенням множини Х в множину У (ф-цією з Х в У) наз правило за яким кожному елем х множ. Х ставить у відповід. єдиний елемент у, що належить множині У.

Позначимо ф-ї або відображення:

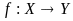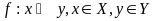1) 2) 3)

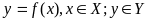
В цьому випадку кажуть, що ф-я задана явно за допомогою формули, яка задає закон відображення.

Елементи 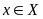-незалежна зміна –аргумент.

х -прообраз елемен. у при відображенні f.

Елемент у = f(х)=У наз. –знач. функції- залежна зміна.

у – образ елемента х при відображ. f.

Х-область визначення функції

У_f-область значень функції

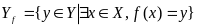-обл знач ф-ції. Отже, Y_f c Y

Розглянемо такі підмножини

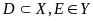
Образом множини D при відображенні f наз. множина f(D)

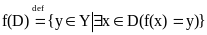
Зауваження:1) f(x) = Y_f – образ мн-ни Х при відображенні f є мн-на Y_{f .}

2)Звуженням ф-ції f на множину D, що належ Х(DєХ) наз ф-ція f_D: D→Y.

Позначимо звуження відображення f на множину

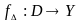
Прообразом множ. Е при відображенні f наз. множина 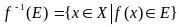Аналогічно познач то тоді

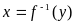
Відображення наз. Ін”єктивним, сюр”активним, бієктивним.

Ін”єктивним –якщо різним значенням аргумента відповідають різні значення ф-ції, або якщо для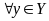 р-ня f(х)=у має більше ніж один корінь

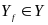
Відображення 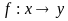назив. сюр”єктивним якщо обл з-нь відображень збігається з 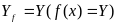або якщо р-ня f(x)y=y має хоч 1 розв-к.

Відображення наз. бієктивним відображенням х на у якщо воно ін”єктивне і сур”єктивне одночасно або якщо для будь якого у є У р-ня f(х)=У має єдиний розв’язок.

Графіком відображ. наз мн-на

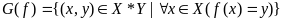
56. Складена, обернена функція.

Нехай задана ф-ція f: X → Yта g: Y→ Z. Композицією ф-ій f і g наз відображення F:X→Z, яке діє з X в Z, причому будь-якому хєХ ставиться у відповідність єдине z=g(f(x))

Позначення: 1) F(x) = g(f(x)) 2) F(x) = (g o f)(x)

Оз: Нехай задано відображення f: X → Y– бієкція. Тоді можна ввести обернену ф. f^-1 : X → Y і задавати таким способом: 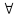у є У 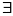!х є Х таке, що х = f^-1 (у).

f і f^-1 – взаємно обернені.

f(f^-1 (у)) = у у є У. f(f^-1 (х)) = х х є Х.

Зауваження: 1) якщо ін’єкція, то будуть f^-1 : У_f →Х

2)Якщо сюр*єкція, то обернена ф-ція є багатозначною. Одержану многозначну ф-цію замінюють на сукуп однозначних ф-цій, які вже будуть оберненою до даної.

57. Параметричне та неявне відображення.

Нехай задано відображення φ: Т →Х. Ψ:Т→У та принаймні 1 з них – бієкція. Нехай φ - бієкція. Тоді існує φ^-1: Х → Т. Утворимо композицію відображень:Ψ_о φ^-1(внутрішня функція):Х(початкова ф-ція)→У(кінцева ф-ція). Таким чином задане від-ння назв ідо-нням, що задано параметрично.

Т – множина значень параметра.

О з:Нехай задано відображення F: XхУ → Z (декартовий добуток мн-н) та р-ня F(x,y)=z (z є Z).

Оз: нехай кожному значенню хєХ відповідає єдине у=f(x) є У таке, що виконується F(x,f(x))=z , то, кажуть, що ф-ція f:X→Y задано неявно рівнянням F(x,y)=z

58. Аксіоми множин дійсних чисел

Оз: під множиною R дійсних чисел розуміють множину, що складається більше ніж з одного елемента та задовольняє аксіомам I-V. Елементи цієї множини називаються дійсними числами

І. Аксіоми додавання:

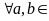R ставиться у відповідність єдине дійсне число 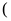a+b), яке наз сумою цих чисел і таке, що при цьому виконується:

I_1. a+b = b+a (комутативність)

Ι₂. (a+b)+c = a+(b+c) (асоціативність)

I₃. 0 R таке, що а+0=а

Ι_4. а R (-а), яке назив протилежним таке, що а+(-а)=0.

а,b R різниця дійсних чисел а і b наз число : а- b= а+(- b)

ΙI. Аксіоми множення: R існує єдине число, що називається добутком цих чисел і позн. аb R так , що виконується:

II_1. ab = ba

II₂. (ab)с = a(bс)

II₃. 1 R така, що а*1=а

II₄. а R, а 0, (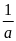 ) R такий , що а* =1

Часткою дійсних чисел а,b не= 0 наз число а/b=a*1/b

ΙΙΙ. Аксіома зв’язку операцій додавання і множення а,b,с R

(а+b)с= ас + bс дистрибутивність

4. Аксіоми впорядкованості а,b R, а і b-різні, виконується а>в або а< b. Притому виконується:

ΙV₁. а< b b< с а<с – транзитивність

ΙV₂. а< b, с R а+с< b+с

ΙV₃. а< b с R с>0 ас< bс

Зауваження:Впорядкованість а b означ,що(а< b)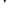 ( а= b)-викон ΙV₁ –ΙV₃

Крім того має місце а а – рефлексивність

а b і b а, то а= b – анти симетричність

V. аксіома неперервності: для двох непорожніх числових множин X,Y R таких, що x X, y Y x y існує с R таке, що x с y

Зауваження:1) з аксіом ΙV₂ і ΙV₃ випливає властивість щільності множини дійсних чисел:для будь-яких різних а,b R,а< b існує с R таке,що а<с<b Доведення: дійсно а<b. 2а< а+b і а+b<2b

2а< а+b<2b а<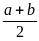 <b , де = с

2)якщо R ={0}, то аксіоми будуть задовольнятися, але ми не будемо мати множину дійсних чисел.