- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •9. Лінійно незалежні системи векторів. Базис,
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини
- •17. Кут між двома площинами.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •29. Обернена матриця.
- •30. Блоковіматриці.
- •31.Розв’язуванняматричнихрівнянь.
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •39. Вимірн і базис вект пр. Перет коорд при пер до нового базису.
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43. Підпрос, утворений розв’язками однорідної с л р. Фундаментальна ср.
- •44 Неоднорідні сис-и лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
52 Зведення кф до канонічного вигляду
Канонічним виглядом квадратичної форми рангу називається представлення її алгебраїчною сумою квадратів:
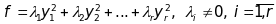 .
(42)
.
(42)
Коефіцієнти називаються канонічними коефіцієнтами. Рівність (42) можна переписати наступним чином:
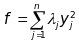 ,
(43)
,
(43)
де
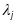 - не всі ненульові (кількість ненульових
коефіцієнтів дорівнює рангу форми).
- не всі ненульові (кількість ненульових
коефіцієнтів дорівнює рангу форми).
Теорема. Будь-яку квадратичну форму ортогональним перетворенням можна звести до канонічного вигляду.
Нехай - ортогональна матриця, тобто , та складається з ортонормованих власних векторів, що відповідають власним значенням матриці квадратичної форми , тому
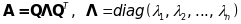 ,
,
де - власні значення матриці . Тоді
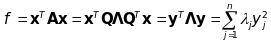 ,
,
де
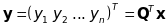 .
Отже, квадратична форма за допомогою
ортогонального перетворення
.
Отже, квадратична форма за допомогою
ортогонального перетворення
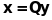 зведена до канонічного вигляду.
зведена до канонічного вигляду.
Зауважимо, що звести квадратичну форму до канонічного вигляду можна і так званим методом Лагранжа або методом виділення повних квадратів.
Нехай
квадратична форма зведена до канонічного
вигляду (42), причому відмінні від нуля
канонічні коефіцієнти занумеровані
так, що
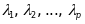 є додатними, а
є додатними, а
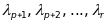 - від’ємними. За допомогою невиродженого
лінійного перетворення змінних
- від’ємними. За допомогою невиродженого
лінійного перетворення змінних
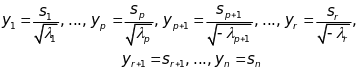
Квадратичну форму можна звести до вигляду:
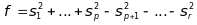 ,
(44)
,
(44)
який називається нормальним виглядом квадратичної форми.
Теорема (закон інерції квадратичних форм). Кількість доданків з додатними (від’ємними) коефіцієнтами в нормальному вигляді квадратичної форми не залежить від способу зведення форми до цього вигляду.
53) Поняття множини. Рівність множин.
Множина- первинне визначення математичного аналізу. Поняття множини вважається первісним і інтуїтивним. Елемент відноситься до певної множини за встановленим правилом або характерної ознакою.
А={а}, де А скл з множ. з 1 елемента а малого. Множину можна задавати за допомогою переліку її елементів А={а ,в, с...}
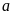 є
А-
елемент а належить множині А.
є
А-
елемент а належить множині А.
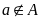 -
а не належить множині А
-
а не належить множині А
Елементи множини А, що мають власн. Р
А1={а
єА
 (а має вл. Р)}
(а має вл. Р)}
А1
={а:
(а є А)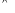 (а
має вл. Р)}
(а
має вл. Р)}
Оз:
мн-на
В
наз.
підмножиною
мн-ни А, якщо всі елементи В належать
мн-ні А.
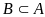 В підмножина А.
В підмножина А.
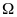 -
універсальна множина, яка включає в
себе всі інші множини.
-
універсальна множина, яка включає в
себе всі інші множини.
Порожньою множиною наз. множина, що не містить жодного елемента.
Множина А і В наз рівними, якщо вони містять одні й ті самі елементи
А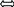 =В (А
=В (А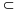 В)
(В
А)
В)
(В
А)
Позначення
Множина натуральних чисел : N= {1,2,3…}
Z0- множина не „-” цілих чисел Z0- {0,1,2,3…}
Z- {0, 1, 2…} – цілих чисел
Q=
{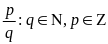 }
Q-
раціональні
}
Q-
раціональні
І- нескінченні неперіодичні дроби.
R – Q + I
С- комплексні
На множину натуральних чисел вводиться операція „+”і виконуються такі влас. (аксіоми):
якщо n є N ( n +1) є N
1 є М (деяка множина), (n є М ( n +1) є М ) N М- аксіома індукції
54) Операції над множинами.
Перерізом множин А і В наз. мн-на, що скл із спільних ел множин А і В
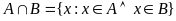
Для ілюстрації операції викор. круги Ейлера або діаграми Вєна.
Об’єднана
множина А
і В,
наз. множина яка містить тільки ті
елементи, які належать А
або належать В
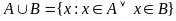
Різницею множини А і В наз. множина, яка містить тільки ті елементи, що належать А і не належать В .
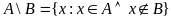 ;
;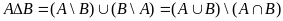 -симетрична
різниця
-симетрична
різниця
Доповненням
множ. А наз. множ. , яка містить тільки
ті елементи, що не належать А.
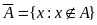
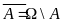
Поняття перерізу і об’єднання мн-н можна поширити на декілька мн-н
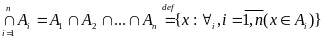
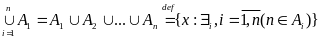
Властивості операцій над множинами:
1)
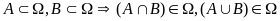 -
ця властивість означає, що відносно
операц. Перерізу та об’єднання
є замкненою.-комутативніс
-
ця властивість означає, що відносно
операц. Перерізу та об’єднання
є замкненою.-комутативніс
2)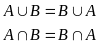 -асоціативність3)
-асоціативність3)
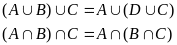 -дистрибутивн.
-дистрибутивн.
4)
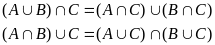 5)
5)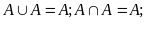
6)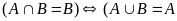 )
8)
)
8)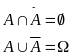
7)
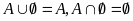
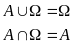 9)
9)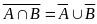 Правило деМоргана
Правило деМоргана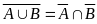
Порядкованою
парою елементів а
є А, в є В, наз.
послідовність (а,
в),
якщо чітко вказано номер компоненти.Декартовим
добутком множ. А і В наз. множина всіх
впорядкованих пар елементів множин А
і В.