
- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •9. Лінійно незалежні системи векторів. Базис,
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини
- •17. Кут між двома площинами.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •29. Обернена матриця.
- •30. Блоковіматриці.
- •31.Розв’язуванняматричнихрівнянь.
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •39. Вимірн і базис вект пр. Перет коорд при пер до нового базису.
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43. Підпрос, утворений розв’язками однорідної с л р. Фундаментальна ср.
- •44 Неоднорідні сис-и лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
44 Неоднорідні сис-и лінійних рівнянь. Теорема Кронекера-Капеллі
Якщо Ах=b , , то система називається неоднорідною.
Теорема Кронекера-Капеллі
Для
того, щоб система
була сумісною, необхідно і достатньо,
щоб ранг матриці системи дорівнював
рангу розширеної матриці системи, тобто
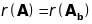 .
Доведення:
r(A)=r(Ab)
<=> b
– лінійна комбінація стовбців А, тобто
коефіцієнт цієї лінійної комбінації і
є розв. с-ми .
.
Доведення:
r(A)=r(Ab)
<=> b
– лінійна комбінація стовбців А, тобто
коефіцієнт цієї лінійної комбінації і
є розв. с-ми .
Теорема
Загальний розв’язок неоднорідної
системи
дорівнює сумі загального розв’язку
відповідної однорідної системи і
окремого розв’язку неоднорідної
системи. Дов:
Нехай
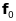 - окремий розв’язок неоднорідної системи
,
- окремий розв’язок неоднорідної системи
,
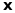 - загальний розв’язок однорідної системи
,
то
- загальний розв’язок однорідної системи
,
то
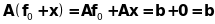 .
Отже,
.
Отже,
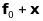 є загальним розв’язком неоднорідної
системи.
є загальним розв’язком неоднорідної
системи.
Теорема: Всі розв’язки неодно-ної сис-ми утворюють в афінному просторі площину вимірності .
Рівняння
цієї площини
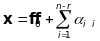 ,
де
- окремий розв’язок неоднорідної
системи,
,
де
- окремий розв’язок неоднорідної
системи,
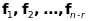 - фундаментальна система розв’язків
відповідної однорідної системи, а числа
- фундаментальна система розв’язків
відповідної однорідної системи, а числа
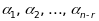 є довільними.
є довільними.
Теорема:
В
афінному просторі
і в будь-яких афінних координатах усяка
-вимірна
площина може бути задана системою
з матрицею
рангу
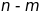 .
.
Наслідок:
Гіперплощина
визначається одним лінійним рівнянням
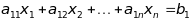 .
Кожне з рівнянь системи
з матрицею
рангу
можна розглядати як рівняння деякої
гіперплощини і кожну
-вимірну
площину можна розглядати як перетин
гіперплощин.
.
Кожне з рівнянь системи
з матрицею
рангу
можна розглядати як рівняння деякої
гіперплощини і кожну
-вимірну
площину можна розглядати як перетин
гіперплощин.
45.Лп та їх матриці. Дії над лп. Обернене лп.
Лінійним
перетворенням
у векторному просторі
називається правило, за яким кожному
вектору
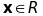 ставиться у відповідність вектор
ставиться у відповідність вектор
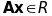 так, що виконуються наступні умови:
так, що виконуються наступні умови:
для будь-яких векторів
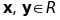 виконується
виконується
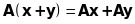 ;
;для будь-якого вектора та довільного числа
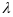 виконується
виконується
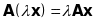 .
.
Лінійне
перетворення
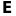 наз тотожнім,
якщо воно перетворює вектор в самого
себе, тобто
наз тотожнім,
якщо воно перетворює вектор в самого
себе, тобто
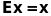 .
.
Сумою
лінійних перетворень
і
наз л п
 ,
що визначається рівністю
,
що визначається рівністю
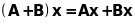 .
.
Добутком
лінійного
перетворення
на число
наз л п
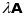 ,
що визначається рівністю
,
що визначається рівністю
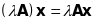 .
.
Добутком
л
п
та л п
наз л п
,
що визначається рівністю
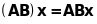 .
.
Зауважимо,
що у загальному випадку
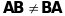 .
.
Операція множення лінійних перетворень має такі властивості:
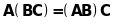 ;
;
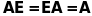 ;
;
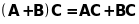 ;
;
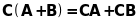 .
.
Лінійне
перетворення
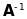 називається оберненим
по відношенню до лінійного перетворення
,
якщо виконуються рівності:
називається оберненим
по відношенню до лінійного перетворення
,
якщо виконуються рівності:
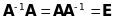 .
.
46.Матриці лп. Подібні матриці.
Нехай
у векторному просторі
,
базис якого
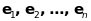 ,
задано лінійне перетворення
.
Застосуємо це перетворення до базисних
векторів. Одержимо
,
задано лінійне перетворення
.
Застосуємо це перетворення до базисних
векторів. Одержимо
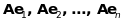 - вектори простору
.
Розкладемо їх за базисом:
- вектори простору
.
Розкладемо їх за базисом:
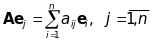 ,
(25)
,
(25)
Матриця
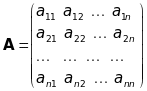 називається матрицею
лінійного перетворення
в базисі
.
називається матрицею
лінійного перетворення
в базисі
.
Позначимо
через
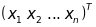 і
і
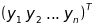 матриці-стовпці координат векторів
і
матриці-стовпці координат векторів
і
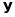 у базисі
простору
.
Припустимо, що
у базисі
простору
.
Припустимо, що
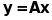 ,
тоді за означенням лінійного перетворення
маємо:
,
тоді за означенням лінійного перетворення
маємо:
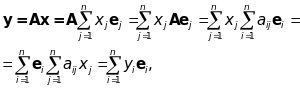
звідки
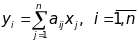 .
(26)
.
(26)
Отже,
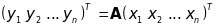 ,
(27)
,
(27)
тобто
будь-якому лінійному перетворенню
у вибраному базисі відповідає квадратна
матриця
,
причому
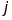 -й
стовпець матриці
складається з координат вектора
-й
стовпець матриці
складається з координат вектора
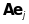 (образу базисного вектора
(образу базисного вектора
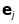 при
перетворенні
)
і
навпаки.
при
перетворенні
)
і
навпаки.
Теорема. Якщо у векторному просторі задано базис та деяку невироджену матрицю -го порядку, то існує єдине лінійне перетворення, матриця якого дорівнює у базисі .
Розглянемо матриці лінійного перетворення в різних базисах.
Нехай
в просторі
задано «старий» базис
і «новий» базис
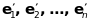 .
Запишемо лінійне перетворення у цих
базисах:
;
.
Запишемо лінійне перетворення у цих
базисах:
;
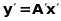 ,
де
і
,
де
і
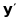 - матриці-стовпці, складені з координат
векторів
і
у базисі
;
а
- матриці-стовпці, складені з координат
векторів
і
у базисі
;
а
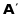 - матриця лінійного перетворення в цьому
базисі. На підставі формули перетворення
координат при зміні базису маємо:
- матриця лінійного перетворення в цьому
базисі. На підставі формули перетворення
координат при зміні базису маємо:
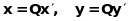 .
Тоді
.
Тоді
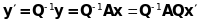 ,
отже
,
отже
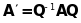 .
(28)
.
(28)
Матриці і називаються подібними і перехід від до називається перетворенням подібності, якщо має місце формула (28), де - невироджена матриця.
Отже, дві матриці, відповідні до одного і того ж лінійного перетворення в різних базисах подібні між собою, причому матриця є матрицею перетворення координат при переході від «старого» базису до «нового».
