
- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •9. Лінійно незалежні системи векторів. Базис,
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини
- •17. Кут між двома площинами.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •29. Обернена матриця.
- •30. Блоковіматриці.
- •31.Розв’язуванняматричнихрівнянь.
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •39. Вимірн і базис вект пр. Перет коорд при пер до нового базису.
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43. Підпрос, утворений розв’язками однорідної с л р. Фундаментальна ср.
- •44 Неоднорідні сис-и лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
42.Ранг матриці.
Нехай
задана
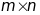 -матриця
-матриця
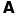 .
Будемо розглядати стовпці
як вектори арифметичного простору
.
Будемо розглядати стовпці
як вектори арифметичного простору
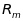 ,
а рядки – як вектори простору
.
Можна вивчати лінійну залежність і
незалежність стовпців (рядків) матриці
.
,
а рядки – як вектори простору
.
Можна вивчати лінійну залежність і
незалежність стовпців (рядків) матриці
.
Мінором
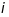 -го
порядку мат
наз визначник
-го
порядку з елем, розміщеними на перетині
будь-яких
-го
порядку мат
наз визначник
-го
порядку з елем, розміщеними на перетині
будь-яких
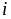 стовпців та будь-яких
рядків матриці
.
стовпців та будь-яких
рядків матриці
.
Рангом
матриці
називається максимальний порядок
відмінних від нуля мінорів матриці.
Ранг матриці
позначається через
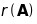 .
Ранг нульової матриці дорівнює нулю,
крім того, ранг задовольняє нерівностям:
.
Ранг нульової матриці дорівнює нулю,
крім того, ранг задовольняє нерівностям:
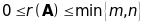 .
.
Будь-який відмінний від нуля мінор порядку наз базисним мінором, а стовпці і рядки - базисними. Зауважимо, що у матриці базисний мінор може бути не один, крім того, будь-яка не 0 матриця має принаймні один базисний мінор.
Т: Базисні стовпці (рядки) матриці лінійно незалежні і будь-який стовпець (рядок) є лінійною комбінацією базисних стовпців (рядків).
Висновки: 1)вимірність підпростору, породженого деякою системою векторів = рангу матриці, складеної з координат цих векторів відносно будь-якого базису; 2)max кількість лінійно незалежних стовпців (рядків) матриці дорівнює рангу матриці.
Т:.
Для того, щоб визначник матриці
порядку
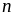 не =0,
необ і дост, щоб його стовпці (рядки)
були лінійно незалежними.
не =0,
необ і дост, щоб його стовпці (рядки)
були лінійно незалежними.
Ефективним заходом при визначенні рангу ненульової -матриці є зведення її за допомогою елементарних перетворень з рядками до ступінчастої матриці, яка має таку будову: 1)ненульові рядки розміщені вище нульових; 2)кожний провідний елемент, який є першим ненульовим елементом у своєму рядку дорівнює одиниці; 3)кожний провідний елемент розміщений праворуч від провідного елемента попереднього рядка.
Якщо
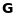 - ступінчаста матриця, то
- ступінчаста матриця, то
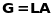 ,
(18)
,
(18)
де
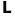 - добуток елементарних матриць, які
відповідають елементарним перетворенням
рядків матриці
.
Елементарні перетворення не змінюють
ранг матриці, тому
- добуток елементарних матриць, які
відповідають елементарним перетворенням
рядків матриці
.
Елементарні перетворення не змінюють
ранг матриці, тому
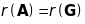 .
Зауважимо, що ранг матриці
дорівнює кількості її ненульових рядків.
.
Зауважимо, що ранг матриці
дорівнює кількості її ненульових рядків.
Теорема.
Для
-матриці
рангу
 існують такі невироджені матриці
і
існують такі невироджені матриці
і
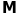 порядків
і
відповідно, що
порядків
і
відповідно, що
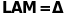 ,
(19)
,
(19)
де
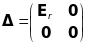 .
.
Теорема. Ранг добутку двох матриць не є більшим ніж ранг кожного множника, тобто
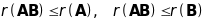 .
(20)
.
(20)
Розглянемо
матрицю
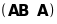 .
Очевидно, що
.
Очевидно, що
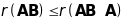 .
Але стовпці матриці
.
Але стовпці матриці
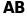 є лінійними комбінаціями стовпців
матриці
,
тому
є лінійними комбінаціями стовпців
матриці
,
тому
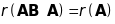 .
Отже,
.
Отже,
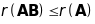 .
.
Наслідок. Множення будь-якої матриці на невироджену матрицю не змінює її ранг.
Нехай
матриця
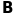 невироджена. На підставі (20) маємо:
невироджена. На підставі (20) маємо:
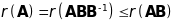 ,
але
,
тому
,
але
,
тому
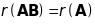 .
.
43. Підпрос, утворений розв’язками однорідної с л р. Фундаментальна ср.
Розглянемо
систему
лінійних алгебраїчних рівнянь
відносно невідомих
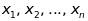 :
:
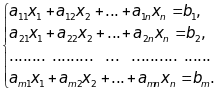 (21)
(21)
Позначимо
через
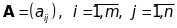 ,
матрицю
системи,
,
матрицю
системи,
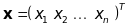 - вектор невідомих,
- вектор невідомих,
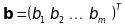 - вектор вільних членів. Тоді система
(21) набуде вигляду
- вектор вільних членів. Тоді система
(21) набуде вигляду
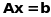 .
Введемо розширену
матрицю системи
.
Введемо розширену
матрицю системи
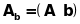 ,
яка отримується з матриці системи
приєднанням до неї стовпця вільних
членів.
,
яка отримується з матриці системи
приєднанням до неї стовпця вільних
членів.
Упорядкована сукупність значень невідомих , яка задовольняє кожному з рівнянь (21), називається розв’язком системи. Якщо система має принаймні один розв’язок, то вона називається сумісною. У противному випадку вона називається несумісною. Якщо система сумісна, то кожний її розв’язок називається окремим. Сукупність всіх окремих розв’язків називається загальним розв’язком системи.
Однорідною
називається така система лінійних
рівнянь, в якій всі праві частини
дорівнюють нулю, тобто
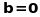 .
Якщо
.
Якщо
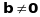 ,
то система називається неоднорідною.
,
то система називається неоднорідною.
Зауважимо,
що однорідна система завжди сумісна,
бо вона має розв’язок
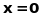 .
Цей розв’язок називається тривіальним
(нульовим)
розв’язком системи
.
Цей розв’язок називається тривіальним
(нульовим)
розв’язком системи
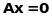 .
.
Теорема.
Якщо
є
-матрицею
рангу
,
то множина всіх розв’язків системи
утворює
 -вимірний
підпростір простору
.
-вимірний
підпростір простору
.
Очевидно,
що коли
 і
і
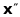 є
розв’язками системи
,
то
є
розв’язками системи
,
то
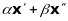 теж є розв’язком цієї системи, тобто
множина розв’язків утворює підпростір
простору
.
Базис цього підпростору називається
фундаментальною
системою
розв’язків.
теж є розв’язком цієї системи, тобто
множина розв’язків утворює підпростір
простору
.
Базис цього підпростору називається
фундаментальною
системою
розв’язків.
