
- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •9. Лінійно незалежні системи векторів. Базис,
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини
- •17. Кут між двома площинами.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •29. Обернена матриця.
- •30. Блоковіматриці.
- •31.Розв’язуванняматричнихрівнянь.
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •39. Вимірн і базис вект пр. Перет коорд при пер до нового базису.
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43. Підпрос, утворений розв’язками однорідної с л р. Фундаментальна ср.
- •44 Неоднорідні сис-и лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
41.Афінний простір...
Множина
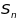 називається
-вимірним
афінним простором,
а її елементи – точками
цього простору, якщо кожній упорядкованій
парі елементів
називається
-вимірним
афінним простором,
а її елементи – точками
цього простору, якщо кожній упорядкованій
парі елементів
 зіставляється єдиний вектор з
зіставляється єдиний вектор з
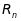 (який позначається через
(який позначається через
 )
у відповідності до аксіом: -для кожної
точки
)
у відповідності до аксіом: -для кожної
точки
 і кожного вектора
і кожного вектора
 існує єдина точка
існує єдина точка
 така, що
така, що
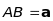 ;
-для будь-яких трьох точок
;
-для будь-яких трьох точок
 виконується
рівність
виконується
рівність
 .
.
Зауважимо,
що векторний простір
можна розглядати як афінний простір
.
Для цього достатньо вектори назвати
точками і кожній парі векторів
зіставити вектор
 .
.
З іншого
боку, афінний простір
можна розглядати як векторний. Для цього
достатньо в просторі
вибрати яку-небудь точку
 і довільній точці
і довільній точці
 зіставити вектор
зіставити вектор
 ,
який називають радіусом-вектором
точки
,
який називають радіусом-вектором
точки
 .
Множина радіус-векторів усіх точок
простору
утворює простір
.
.
Множина радіус-векторів усіх точок
простору
утворює простір
.
Введемо поняття афінних координат точок . Для цього виберемо в деяку точку , яку називають початком координат, і в просторі візьмемо деякий базис . Початок координат разом з базисом утворюють афінну систему координат в афінному просторі.
Розклавши радіус-вектор довільної точки за базисом , одержимо:
 .
.
Коефіцієнти
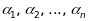 цього розкладу називаються афінними
координатами
точки
відносно вибраної афінної системи
координат. Ці координати визначаються
однозначно, оскільки єдиним є розклад
вектора
за базисом
.
цього розкладу називаються афінними
координатами
точки
відносно вибраної афінної системи
координат. Ці координати визначаються
однозначно, оскільки єдиним є розклад
вектора
за базисом
.
Очевидно, що
 ,
,
де
- афінні координати точки
 .
.
Якщо в
афінному просторі
зафіксована деяка точка
 і у векторному просторі
вибраний
-вимірний
підпростір
і у векторному просторі
вибраний
-вимірний
підпростір
 ,
то множина всіх точок
,
для яких
,
то множина всіх точок
,
для яких
 ,
називається
-вимірною
площиною,
що проходить через точку
в напрямі підпростору
.
Точки
і
називаються відповідно початковою
і поточною
точками
площини, а
- напрямним
підпростором
цієї площини.
,
називається
-вимірною
площиною,
що проходить через точку
в напрямі підпростору
.
Точки
і
називаються відповідно початковою
і поточною
точками
площини, а
- напрямним
підпростором
цієї площини.
При
 площина складається лише з точки
(нульвимірна площина). Одновимірна
площина називається прямою
лінією.
Площина вимірності
площина складається лише з точки
(нульвимірна площина). Одновимірна
площина називається прямою
лінією.
Площина вимірності
 називається гіперплощиною,
а при
називається гіперплощиною,
а при
 площина збігається з усім простором
.
площина збігається з усім простором
.
Нехай
в просторі
вибрана деяка афінна система координат
з початком
і базисом
.
Розглянемо площину, що проходить через
точку
в напрямі підпростору
.
Якщо
породжується лінійно незалежними
векторами
 ,
то радіус-вектор
поточної точки площини дорівнює (рис.
1)
,
то радіус-вектор
поточної точки площини дорівнює (рис.
1)
 ,
(12)
,
(12)
де
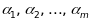 - параметри, які приймають усякі числові
значення. Якщо позначити
- параметри, які приймають усякі числові
значення. Якщо позначити
 ,
то одержимо векторне
рівняння
-вимірної
площини:
,
то одержимо векторне
рівняння
-вимірної
площини:
 .
(13)
.
(13)

Рис. 1
Якщо
введені вектори
 розкладені за базисом
,
тобто
розкладені за базисом
,
тобто
 ,
то одержимо параметричні
рівняння
площини в заданій системі координат:
,
то одержимо параметричні
рівняння
площини в заданій системі координат:
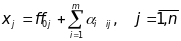 .
(14)
.
(14)
Якщо
 ,
то (14) є рівнянням напрямного підпростору
.
,
то (14) є рівнянням напрямного підпростору
.
У випадку
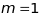 маємо векторне рівняння прямої лінії:
маємо векторне рівняння прямої лінії:
 (15)
(15)
і її параметричні рівняння:
 .
(16)
.
(16)
Якщо
з параметричних рівнянь виключити
параметр
 ,
то одержимо канонічні
рівняння
прямої лінії:
,
то одержимо канонічні
рівняння
прямої лінії:
 .
(17)
.
(17)
