28. Аппроксимация кривых разгона методом площадей.

В основе метода лежит предположение, что исследуемый объект регулирования может быть описан линейным дифференциальным уравнением с постоянными коэффициентами:

Где - постоянные коэффициенты. Передаточная функция объекта, описываемого уравнением (2.18) может быть представлена как

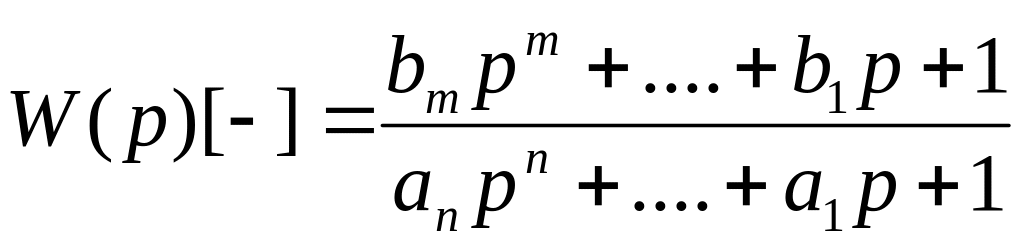(2.19) или в размерной форме

(2.20)

Задача состоит в том, чтобы определить неизвестные коэффициенты , используя для этого систему уравнений (2.21). В Этой системе уравнений и для всех значений

(2.21)

Входящие в данную систему уравнений коэффициенты вычисляются по следующим формулам:

(2.22)

Эти коэффициенты получили название «площадей». Для F₁ – это действительно геометрическая площадь (рис. 2.15), а для остальных коэффициентов это название условно. В формулах (2.22) введена новая переменная .

В практике чаще всего встречаются следующие объекты:

1. Объекты с самовыравниванием без транспортного запаздывания;

2. Объекты без самовыравнивания и без транспортного запаздывания;

3. Объекты обоих видов, но с транспортным запаздыванием.

29. Характер движения в нелинейных и линейных сар.

НСАР называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением.

Процессы в НСАР имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах. Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным. Кроме структуры системы значений ее параметров для устойчивости того или иного установившегося процесса имеют значение здесь, в отличие от нелинейных систем, также и начальные условия. Возможен новый вид установившегося процесса – автоколебания, т.е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным.

Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям (зоны застоя области с различной топологией фазовых траекторий, разделяемые сепаратрисами и т.д.).

Если процессы в системе имеют вид, указанный на рис. а), то равновесное состояние системы (х=0) неустойчиво. В том случае, когда оба указанных на рис .а) колебания в переменных процессах стремятся к одной и той же амплитуде и частоте, система будет обладать устойчивыми автоколебаниями с амплитудой «а».

На рис. б) показан случай, когда равновесное состояние (х=0) системы устойчиво «в малом», т.е. при начальных условиях, не выводящих отклонения в переходном процессе за определенную величину «а», и неустойчива «в большом», т.е. при начальных условиях, выводящих отклонения в переходном процессе за пределы величины «а». здесь граничным процессом является неустойчивый периодических процесс собственного движения системы с амплитудой «а» (переходные процессы расходятся от него в обе стороны).

На рис. в) показали случай трех возможных установившихся состояний: 1) равновесное состояние (х=0), 2) колебания с постоянной амплитудой а_{1, 3)} колебания с постоянной амплитудой а₂. При этом колебания с амплитудой а₁ неустойчивы. В результате система будет устойчива «в малом» по отношению к равновесному состоянию х=0, а «в большом» система будет обладать устойчивыми автоколебаниями с амплитудой а₂.