9.Аксиоматика Гильберта III, IV, V группы.

III.Аксиомы конгруэнтности:

1)если дан отрезок АВ и в этой же плоскости или в другой луч А1М,то существует такая точка В,принадл.полупрямой А1М, что АВ конгруэнтно А1В1.

2)если два отрезка конгруэнтны 3-му,то они конгруэнтны между собой.Отношение конгруэнтности явл. отношением эквивалентности на мн-ве всех отрезков.

3)АВ и ВС,А’B’ и B’C’ на прямой,отрезки без внутренних точек.Если АВ конгруэнтно А’B’,BC конгруэнтно B’C’  АС конгруэнтно A’C’.

4) Пусть дан ے(h,k) в плоскости α, а также определённая относительно прямой a' полуплоскость плоскости α', пусть h' – луч прямой a', выходящий из точки O'. Тогда на плоскости α' существует один и только один луч k', такой, что ے(h,k) конгруэнтен ے(h',k') и при этом все внутренние точки ے(h',k') лежат в данной полуплоскости α', это записывается символически: ے(h,k)≡ے(h',k'). Всегда ے(h,k)≡ے(h,k) и ے(h,k)≡ے(k,h).

Следствие. Каждый угол конгруэнтен сам себе.

 5) Если для двух треугольников ABC и A'B'C' имеют место конгруэнции: AB≡A'B', AC≡A'C', ےBAC≡ےB'A'C', то ےABC≡ےA'B'C'

IV. Аксиома параллельности.

Дана прямая b и точка В на прямой,тогда в плоскости,содержащей эту прямуюиточку,существует не более одной прямой,проходящей через В и не пересекающей b.

Эта аксиома вместе со следствием о существовании || прямых означает,что через т-ку В не принадлежащую b проходит одна и только одна прямая b’,не пересекающая b.

V. Аксиома непрерывности:

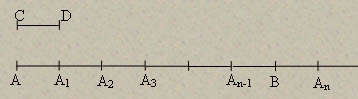
1) Постулат Архимеда. Пусть AB и CD – два произвольных отрезка и пусть на луче AB с вершиной A взяты точки A₁, A₂, A₃,…, расположенные так, что A₁ лежит между A и A₂, точка A₂ лежит между A₁ и A₃ и т. д., причём отрезки AA₁, A₁A₂, A₂A₃,… конгруэнтны отрезку CD. Тогда существует такой номер n, что точка B лежит между A и A_n.

2) Принцип вложенных отрезков Кантора. Пусть на произвольной прямой a дана бесконечная последовательность отрезков A₁B₁, A₂B₂, A₃B₃,…, из которых каждый последующий лежит внутри предыдущего, пусть при этом не существует отрезка, лежащего внутри всех отрезков данной последовательности. Тогда напрямой a существует одна и только одна точка M, лежащая внутри всех отрезков A₁B₁, A₂B₂, A₃B₃,…

10. Аксиоматика Погорелова I, II группы.

I Аксиомы принадлежности:

1. Через 2 точки проходит единственная прямая.

2. Каждая прямая содержит 2 точки и существуют 3 точки не лежащие на одной прямой.

II Аксиомы порядка:

1. Из 3-х точек на прямой одна единственная лежит «между» двумя другими.

2. Если прямая l в пл-ти, то прямая разбивает плоскость на 2 полуплоскости, так что если A и B в одной полупл-ти , то l не пересекает отр АВ. Если А и В в разных полупл-тях, то l пересекает АВ.

Следствие: Из аксиомы II₂ вводится понятие треугольника АВС сост из 3-х отрезков и 3-х точек не лежащих на одной прямой.

11.Аксиоматика Погорелова, 3,4 5,6 группы.Пространственные аксиомы.

3.Аксиомы длины отрезка и меры углов:

3.1Каждый опред.отрезок имеет опред.длинну(не отрицдействит.число)

|АВ|=|АМ|+|МВ|.

После этого логично вывести получ.группы на прямой.Выбираем точку О.

О разбивает прямую на 2 полупрямые L «разбивает плоскость на 2 части».

Одна полупрямая обзн.положительно на пр-р ОА, вторая ОС-отрицательной, тогда х точки, А – длинна отрезка|ОА|,х-точки х_С=-|ОС|

3.2Каждый угол имеет опр. меру 0<Q<180. Каждый угол имеет определенную гр-ную меру.

<hl=r=Q, 0<Q<180. Если m между hиl,

о <hm+<ml=<hl или α+β=γ

Свойство аддитивности:

- разверн. угол,<hl=180

A h,B l.Если луч не пересекает АВ, то это и означает что m «между» h и l.

В треуг. АВВ₁ m пересекает АВ m пересечет АВ(m проходит через О и BB₁).m и BB₁ = М₂ в треуг АА₁В₁ m пересекает BB₁ .Независимо от выбора отрезка m пересекает его.