1 Множества и отношения. Примеры.

Если X- мн-ва,то

…= - мн-во всех наборов.

P(x)-мн-ва всех подмножеств Х.

Отношение на множестве Х – это Если , то говорят находится в отношении .

Примеры

1. n=1 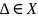наз. Унарное(одинарное) отношение. Это означает, что каждые элементы мн-ва выделены.

2. n=2 бинарное отношение.

1. E– мн-во точек евклидовой плоскости, L – мн-во всех прямых.

(A, ) <=> А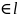 - инциндентность или принадлежность.

2. S – мн-во всех треугольников на плоскости или прстранстве.

Среди бинарных отношений выделяются отношения «эквивалентности» которые удовлетворяют 3 свойствам: рефлексивность, симметричность, транзитивность.

3. n=3 тенарное отношение

E -мн-во точек пространства евклида.

(A,B,M) <=>

4. Отображение (ф-ция)

х,у - множества

f: х -> у х->f(х)=у

гр. Ф-ции.

5. Алгебраические операции определяются через отоброжения и поэтому также явл. отношением .

f:

6. Скалярное произведение

G: ) =

7. Меорина

M – пространство точек

-> - неотрицательные числа

8. Откладывание вектора

E - пространство точек

2. Математические структуры. Примеры

Основным методом в современной математике является аксиоматиче-

ский метод в теоретико-множественном понимании, тесно связанный с поня-

тием математической структуры.

Пусть А1,А2,А3,...,Аn - непустые множества. А1 ЧА2 ЧА3 Ч...ЧАn -

прямое (декартово) произведение этих множеств, т.е. множество всех упоря-

доченных n-местных кортежей (a1;a2;...;an), элемент ai которых, стоящий на

i-ом месте, принадлежит множеству Ai ,i =1,2,...,n.

В теоретико-множественной записи:

А1ЧА2 ЧА3 Ч...ЧА ={(a1,a2,...,an)|ai∈Ai}.

n

Определение 1.1.1. Любое подмножество декартова произведения множеств

А1 ЧА2 ЧА3 Ч...ЧА называется n-арным (или n-местным) отношением δ , nопределенным во множествах А1,А2,А3,...,Аn .

Замечание. Из определения имеем:

1) δ ⊂А1ЧА2 ЧА3 Ч...ЧАn.

2) Элементы (a1;a2;...;an)(ai∈Ai ,i =1,2,...,n) находятся в отношении δ ,ес-

ли (a1;a2;...;an)∈δ .

3) Если А1 = А2 = А3 = ...= Аn = A, то А1 ЧА2 ЧА3 Ч...ЧАn = An - n-аядекар-

това степень множества A.

4) Если δ ⊂An , то говорят: на множестве A определено n-арное отношение

δ .

5) В случае бинарного отношения δ ⊂A1 ЧA2 вместо (a1;a2)∈δ пишут a1δa2

- «a1 находится в отношении δ с a2». Например, отношение равенства на

множестве R всех вещественных чисел – бинарное отношение.

6) Пусть на множестве A определена алгебраическая операция (внутренний

закон композиции)

ϕ : AЧA→A.

Ее можно рассматривать как тернарное отношение δ ⊂AЧAЧA= A3 , где

δ ={(a,b,c)∈A3 |ϕ(a,b) = c}, a,b,c∈A.

7) Пусть на множестве A определен внешний закон композиции f с множе-

ством операторов Λ:

f :ΛЧA→A.

Его можно рассматривать как тернарное отношение, определенное на множе-

ствах Λ,A при помощи подмножества δ ⊂ΛЧAЧA, т.е.

δ ={(λ,a,b)∈ΛЧAЧA| f (λ,a)=b}, λ∈Λ, a,b∈A.

Рассмотрим конечную систему различных непустых множеств

А1,А2,А3,...,Аn . Пусть, например, n= 3.

7 Пусть σ ={δ1,δ2,...,δk} - некоторая система тернарных отношений, оп-

ределенных на множествах А1,А2,А3 и обладающих свойствами α1,α2,...,αt .

То есть δi - это такое подмножество декартова произведения А1ЧА2ЧА3 ,

которое обладает всеми свойствами α1,α2,...,αt одновременно.

Может быть, что существует не одна, а несколько таких систем отно-

шений σ ={δ1,δ2,...,δk}. Например, ϕ - алгебраическая операция на множе-

стве R действительных чисел: ϕ :RЧR→R (т.е. ϕ можно рассматривать

как единственное отношение δ ={(a,b,c)∈R3 |ϕ(a,b)=c}, a,b,c∈R). Пусть

отношение δ обладает свойством коммутативности

α1 :ϕ(a,b)=ϕ(b,a)∀a,b∈R.

Можно указать два знчения отношения δ , обладающего свойством α1 (т.е.

две коммутативные операции на R): δ′ - сложение, δ′′- умножение, т.е.

δ′ ={(a,b,c)∈R3 |a+b=c},

δ′′ ={(a,b,c)∈R3 |a⋅b=c}.

Пусть Τ - непустое множество всех систем σ ={δ1,δ2,...,δk} отноше-

ний, каждое из которых обладает заданными свойствами α1,α2,...,αt .

Определение 1.1.2. Элемент σ∈Τ определяет на множествах А1,А2,А3

математическую структуру рода Τ .

Определение 1.1.3. Явно сформулированные свойства α1,α2,...,αt , оп-

ределяющие множество Τ , называются аксиомами структуры рода Τ .

Определение 1.1.4. Множества А1,А2,А3 называются базой структуры

рода Τ .

Таким образом, математическая структура рода Т представляет со-

бой одно или несколько множеств А1,А2,А3,...,Аn(образующих базу струк-

туры), элементы которых произвольной природы (основные, неопределяемые

понятия данной теории) и находятся в некоторых отношениях

δ1,δ2,...,δ (называемых основными неопределяемыми отношениями), удов-

летворяющих аксиомам α1,α2,...,αt .

Аксиомы иногда характеризуют не одну с точностью до изоморфизма,

а некоторое множество математических структур. Совокупность всех струк-

тур, определенных данной системой аксиом Σ ={α1,...,αt}, называется родом

Т этих структур.

Совокупность предложений, которые можно вывести логическимпу-

тем из аксиом структуры, называется теорией структуры рода Т.

В 30-х годах ХХ в. Н. Бурбаки определил математику как науку о ма-

тематических структурах. Математические структуры подразделены им на

три вида: алгебраические, порядковые и топологические. Евклидово, псевдо-

евклидово, риманово, псевдориманово пространства, пространственно-

временной континуум являются примерами структур топологического типа.

8 Рассмотрим простейшие структуры алгебраического типа. Всем струк-

турам одного и того же рода дают специальное название: структура группы,

структура n-мерного векторного пространства и др.

Пример 1.1.1. (структура группы). Система σ ={δ1,δ2,...,δk} отноше-

ний состоит из одного тернарного отношения δ ⊂GЧGЧG=G3, соответст-

вующего алгебраической операции:

ϕ :GЧG→G

(т.е. ϕ можно рассматривать как единственное отношение

δ ={(a,b,c)∈G3 |ϕ(a,b)=c}, a,b,c∈G). База состоит из одного множества

G . Три аксиомы системы аксиом Σ ={α1,α2,α3} структуры группы:

α : ∀a,b,c∈G:ϕ(ϕ(a,b),c)=ϕ(a,ϕ(b,c)) - аксиома ассоциативности;

1

α2 :∃e∈G∀a∈Gϕ(a,e)=ϕ(e,a)=a - существование нейтрального элемен-

та;

α3 :∀a∈G∃a′∈G ϕ(a,a′)=ϕ(a′,a)=e - существование симметричного

элемента.

Пример1.1.2. (структура n-мерного векторного пространства над заданным

полем).

База состоит из двух множеств – основного множества V (его элементы -

векторы – основные неопределяемые понятия); вспомогательного множест-

ва K(его элементы условно называются скалярами). Система отношений

σ ={δ1,δ2,...,δk} состоит из двух тернарных отношений:

δ1 ⊂KЧVЧV, δ1 ={a, xr, yr | f (a, xr)= yr}, a∈K, xr, yr∈V ;

δ2 ⊂V ЧVЧV =V3, δ2 ={(ar,br,cr)|ϕ(ar,br) = cr}, ar,br,cr∈V .

Аксиомы структуры векторного пространства V над полем K:

α1 :∀λ,μ∈K∀ar∈V f (λ, f (μ,ar)= f (λμ,ar);

α2 :∀λ,μ∈K∀ar∈V f (λ+μ,ar)=ϕ( f (λ,ar), f (μ,ar));

α3 :∀ar∈V f (1,ar)=ar;

α ∀r r∈∀λ∈ λ ϕ r r =ϕ λ r λ r ;

4 :a,b V, K f ( , (a,b)) ( f ( ,a), f ( ,b))

α5 :∃0r∈V ∀ar∈Vϕ(0r,ar) =ϕ(ar,0r) = ar ;

α∀ar∈V∃ −ar∈V ϕar −ar =ϕ −arar = r ;

6 : ( ) ( ,( )) (( ), ) 0

α7 :ϕ(ar,br)=ϕ(br,ar)∀ar,br∈V ;

α8 :ϕ(ar,ϕ(br,cr))=ϕ(ϕ(ar,br),cr)∀ar,br,cr∈V .

Таким образом, теория структур рода Т – это множество предложе-

ний (теорем), являющихся логическими следствиями аксиом структуры рода

Τ .

Предметом математики являются математические структуры. Основ-

ной метод математики – дедуктивный аксиоматический (от общих акси-

ом к частным следствиям из них):

- вводятся неопределяемые, первичные понятия структуры;

- вводятся основные отношения;

- структуры строятся с помощью аксиом;

- затем, используя законы логики, строится теория структур данного рода.