Р исунок 7. 2
В настоящей работе для определения удельного заряда электрона е/т используется цилиндрический магнетрон.
Магнетроном называется двухэлектродная электронная лампа (диод), в которой электроны, летящие от катода к аноду, наряду с электрическим полем, подвергаются действию внешнего магнитного поля. Магнитное поле, направленное вдоль вертикальной оси лампы, создается соленоидом.
Соленоид состоит из большого числа витков изолированной медной проволоки, намотанной на каркас. При пропускании через соленоид электрического тока Iс возникает магнитное поле, которое в средней части соленоида близко к однородному.
Индукцию магнитного поля соленоида можно определить исходя из теоремы о циркуляции для вектора В:
циркуляция вектора B по произвольному замкнутому контору равна алгебраической сумме токов, охватываемых контуром, умноженной на магнитную постоянную μ0 (μ0=4π∙10-7 Гн/м)
(7.
0 )
В качестве контура удобно выбрать прямоугольник бесконечно малой высоты.
Рисунок 7. 3
Тогда
(7. 0)
На участках AB и CD скалярное произведение Bdl равно нулю, так как здесь вектор B перпендикулярен вектору dl . На участке DA скалярное произведение Bdl равно нулю, так как здесь нет поля (все поле сосредоточено внутри соленоида). Таким образом формулу (7.10) можно представить в виде:
(7.
0)
Сумма токов, охватываемых контуром, равна
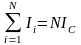(7.
0)
где Iс - сила тока в соленоиде, N- число витков, охватываемых контуром.
Подставляя (7.11) и (7.12) в (7.9), получим:
(7.
0)
Таким образом, индукция магнитного поля бесконечно длинного соленоида, равна:
(7.
0)
где n - число витков на единицу длины соленоида.
Диод представляет собой высоковакуумный баллон с двумя впаянными в него электродами - анодом А и катодом К. Анод имеет форму цилиндра радиуса a. Катод представляет собою полый цилиндр радиуса b , по оси которого расположена вольфрамовая нить - нить накала.
Раскаленный катод испускает термоэлектроны, образующие вокруг катода электронное облако. При создании между анодом и катодом разности потенциалов UA (анодное напряжение), электроны начинают перемещаться от катода к аноду вдоль радиусов, и во внешней цепи лампы возникает анодный ток IA, величина которого зависит от приложенного анодного напряжения. Чем больше анодное напряжение, тем больше электронов в единицу времени достигают анода, следовательно, тем больше анодный ток. При некотором значении анодного напряжения все электроны, вырванные с поверхности металла в результате термоэлектронной эмиссии, достигают анода и при дальнейшем увеличении UA ток не увеличивается, т.е. достигает насыщения.
Для определения удельного заряда электрона магнетрон помещают в поле соленоида так, что лампа находится в центре соленоида, где поле однородно. Магнитное поле соленоида перпендикулярно плоскости, в которой движутся к аноду электроны, вырванные с катода.
В
магнетроне на каждый электрон, движущийся
в лампе по радиусу от катода к аноду, со
стороны магнитного поля соленоида
действует сила Лоренца, определяемая
по формуле (7.2). Так как электроны движутся
радиально, а магнитное поле соленоида
направлено по оси лампы, то угол между
и В
равен
90° и сила Лоренца, действующая на
движущийся электрон, перпендикулярна
и B.
Под действием силы Лopeнцa электроны движутся по криволинейным траекториям, форма которых близка к дуге окружности . С увеличением индукции магнитного поля соленоида (силы тока в соленоиде) радиус траектории уменьшается (см. формулу (7.6)).
Н
а
рис. 7.4 показаны траектории движения
электронов при различных значениях
индукции магнитного поля. Здесь
представлены траектории трех электронов,
вылетающих с поверхности катода с
различными скоростями. При малых полях
все электроны попадают на анод и поэтому
анодный ток остается неизменным при
увеличении, магнитного поля При некотором
поле уже не все электроны попадают на
анод и поэтому анодный ток уменьшается.
Когда ни один электрон не попадает на
анод, ток в анодной части цепи прекращается.
Рисунок 7. 4
Рассмотрим движение электрона в лампе. Разность потенциалов между анодом и катодом лампы постоянна. Вектор напряженности электрического поля E направлен по радиусу от анода к катоду. Электрона, покинувший анод с нулевой скоростью пройдя разность потенциалов U , приобретает скорость
(7.
0)
Введем цилиндрическую систему координат. Направим ось Z вдоль оси лампы. Проекция вектора B на эту ось Bz=B. В перпендикулярной оси Z плоскости положение точек определяется расстоянием от оси r и угол φ.
Проекции
скорости электрона имеют следующий
вид:
(7. 0)
Движение
электрона определяется уравнением
моментов
,
где
L
- момент импульса электрона,
М
- момент силы Лоренца, действующей на
электрон;
Проекция
на ось oz
момента импульса электрона равна
Радиальная и угловая проекции силы Лоренца:
;
Проекция момента силы Лоренца на ось OZ:
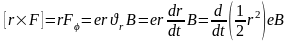
Тогда
уравнение моментов в проекции на ось
имеет вид:
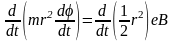
Интегрируя
это уравнение, получим
Постоянная
интегрирования определяется из начальных
условий при
;
Окончательно
получаем
(7. 0)
Когда
магнитное поле достигает критического
значения
, электроны не попадают
на анод. т.е. при
;
тогда
,
подставляя
это значение
в уравнение (7.17), получим
Из этого равенства получаем отношение заряда электрона к его массе (удельный заряд)
(7.
0)
Значение индукции магнитного поля внутри соленоида рассчитывается по формуле
(7.
0)
где
0=
410-7
Гн/м
магнитная
постоянная, I-
ток через соленоид ,
-число
витков
на единицу длины соленоида.