3.5. Функции перв, след и выбор.

Множество ВЫБОР строится для каждого правила и включает те терминальные символы, при появлении которых под читающей головкой распознаватель должен применять это правило.

Для определения множества ВЫБОР используются функции ПЕРВ и СЛЕД . Аргументом функции ПЕРВ может быть любая цепочка полного словаря µ, а значением функции ПЕРВ(µ) является множество терминальных символов, которые могут стоять на первом месте в цепочках, выводимых из цепочки µ.

Построение функции ПЕРВ(µ)   Значение функции ПЕРВ() можно определить пользуясь следующими правилами: 1)  Если цепочка µ начинается терминальным символом и имеет вид bµ', то функция ПЕРВ(µ) = {b},

2)  Если цепочка µ является пустой цепочкой, µ = $, то функция ПЕРВ(µ) = $, 3)   Если цепочка µ начинается нетерминальным символом <B> и имеет вид <B>µ', а в схеме грамматики имеется n  правил, в любой части которых находится символ <B>: <B>   ₁ | ₂ | ... | _n ,

и, если не существует вывода <B> ==>* $, то функция ПЕРВ(<B>µ') представляет собой объединение множеств: ПЕРВ(<B>µ') = ПЕРВ(₁)  ПЕРВ (₂) ...ПЕРВ(_n),

4)   Если цепочка µ начинается нетерминальным символом и имеет вид <B>µ', в схему грамматики входят n правил вида <B>   ₁ | ₂ | ... | _n ,

и <B> является аннулирующим нетерминалом, т.е. существует  <B> ==> *$, то функция

ПЕРВ(<B>µ')=ПЕРВ(µ')  ПЕРВ( ₁) ПЕРВ( ₂) ... ПЕРВ( _n).

В качестве примера выполним вычисление функции ПЕРВ для правил следующей грамматики:

 Г_3.6 :     R = {      (1) <A>   <B><C>c,

(2) <A>   g<D><B>, (3) <B>   $, (4) <B>   b<C><D><E>, (5) <C>   <D>a<B>, (6) <C>   ca, (7) <D>   $, (8) <D>   d<D>, (9) <E>   g<A>f, (10) <E>   c   }.

Вначале найдем значения функции для правых частей правил (2), (4), (6), (8), (9) , (10) , начинающихся терминальными символами:

ПЕРВ(g,<D>,<B>) = {g} ПЕРВ(b<C><D><E>) = {b} ПЕРВ(ca) = {c} ПЕРВ(d<D>) = {d} ПЕРВ(g<A>f) {g} ПЕРВ(c) = {c}

Затем вычислим функцию для правил (5) и (6) :

ПЕРВ (<C>) = ПЕРВ (<D>a<B>)  ПЕРВ (ca).

Учитывая, что <D> является аннулирующим нетерминалом, получаем:

ПЕРВ(<C>) = ПЕРВ(a<B>) ПЕРВ(<D>) {c} = {a}{d}{c}={a,d,c}.

При вычислении функции для правил (1) и (2) также необходимо иметь в виду то, что <B> является аннулирующим терминалом, поэтому имеем:

ПЕРВ(<A>) = ПЕРВ(<B><C>c)  ПЕРВ(g<D><B>) = ПЕРВ(<C>c)  ПЕРВ(<B>)  ПЕРВ(g<D><B>) =

{a,d,c}  {b} {g} = {a,b,c,d,g}.

22. Функция СЛЕД. Аргументы. Значения. Правила вычисления.

Построение функции СЛЕД(<B>)  

Аргументом функции СЛЕД является нетерминальный символ, например <B>, а значение функции СЛЕД(<B>) представляет собой множество терминалов, которые могут следовать непосредственно за нетерминалом  <B>  в цепочках, выводимых из начального символа грамматики. Вычисление значения функции СЛЕД(<B>) должно выполняться  по следующим правилам: 1)    Если в схеме грамматики имеются правила вида

<X₁>   µ₁<B>₁,  <X₂>   µ₂<B>₂, ... , <X_n>   µ_n<B>_n,  и все цепочки  _i/$ , то

СЛЕД(<B>) = ПЕРВ( ₁)  ПЕРВ( ₂)  ...  ПЕРВ( _n).  2)   Если же среди приведенных выше правил имеется хотя бы одна цепочка _i = $, например пусть ₁ = $, то функция вычисляется так:

СЛЕД(<B>) = СЛЕД(<X₁>)  ПЕРВ( ₂)  ...  ПЕРВ( _n).

Выполним вычисление функции СЛЕД для нетерминалов грамматики Г_3.6 . Вначале определим функцию для нетерминала <A>, который встречается в правой части правила (9).           СЛЕД(<A>) = ПЕРВ(f) = {f}. Нетерминал <C> входит в правые части правил (1) и (4), учитывая также, что нетерминал <D> являетя анулирующим, получаем:

СЛЕД(<C>) = ПЕРВ(<D>)  ПЕРВ(<E>) ПЕРВ(c) = {c,d,g}.

Нетерминал <B> входит в правые части правил (1), (2), (5), поэтому имеем:

СЛЕД(<B>) =ПЕРВ(<C>c)  СЛЕД(<A>)   СЛЕД(<C>),

подставляя в полученное выражение значения функций, входящих в правую часть, получаем:

СЛЕД(<B>) = { a, c, d, } { f }  U { c, d, g, } = { a, c, d, g, f }.

Для нетерминала <D> , который входит в правила (2), (4) , (5) и  (8), с учетом того, что нетерминал <B> является аннулирующим, получаем:

СЛЕД(<D>) =ПЕРВ(<B>)  СЛЕД(<A>)   ПЕРВ(<E>)  ПЕРВ(a<B>),

учитывая, что , для нетерминала <E>, входящего в правило (4)           СЛЕД(<E>) = СЛЕД(<B>) = {a,d,c,g,f}, окончательно имеем:           СЛЕД(<D>) = ПЕРВ(<B>) СЛЕД(<A>) ПЕРВ(<E>)  {a} =

= {b} {f}  {c,g}  {a} = {a,b,c,g,f}.

23. Функция ВЫБОР. Аргументы. Значения. Правила вычисления.

Построение функции ВЫБОР.  

Функция ВЫБОР, которая потребуется нам для построения переходов магазинных автоматов,можно определить  с помощью функций ПЕРВ и СЛЕД следующим образом:

1)   Если правило грамматики имеет вид <B> - >  и  не является аннулирующей цепочкой, другими словами не существует вывод  ==>*$, то   ВЫБОР(<B>    ) = ПЕРВ(  ).

2)    Для аннулирующих правил грамматики вида <B>  $, мно- жество выбора определяется так   ВЫБОР(<B>   $) = СЛЕД(<B>).

3)    Если правило грамматики имеет вид <B>   µ и µ яв- ляется аннулирующей цепочкой, то

ВЫБОР(<B>   µ) = ПЕРВ(µ)  СЛЕД(<B>).

 Для рассматриваемой грамматики Г_3.6 множества ВЫБОР для каждого из правил, построенные описанным выше способом, имеют вид:

ВЫБОР(<A>   <B><C>c) = ПЕРВ(<B><C>c) = {a,b,c,d}, ВЫБОР(<A>   g<D><B>) = ПЕРВ(g<D><B>) = {g}, ВЫБОР(<B>   $) = ПЕРВ($)  СЛЕД(<B>) = {a,c,d,g,f}, ВЫБОР(<B>   b<C><D><E>) = ПЕРВ(b<C><D><E>) = {b}, ВЫБОР(<C>   <D>a<B>) = ПЕРВ(<D>a<B>) = {a,d}, ВЫБОР(<C>   ca) = ПЕРВ(ca) = {a}, ВЫБОР(<D>   $) = ПЕРВ($)  СЛЕД(<D>) = {a,b,c,g,f}, ВЫБОР(<D>   d<D>) = ПЕРВ(d<D>) = {d}, ВЫБОР(<E>   g<A>f) = ПЕРВ(g<A>f) = {g}, ВЫБОР(<E>   c) = ПЕРВ(c) = {c}.

24. Слабо разделенные грамматики.

Слаборазделенные грамматики

Используя введенные понятия,  можно дать определение слаборазделенной грамматики.  

Определение. КС-грамматика называется слаборазделенной, если выполняются  следующие три условия:   правая часть каждого правила представляет собой либо пустую цепочку $, либо начинается с терминального символа,   если два правила имеют одинаковые левые части, то правые части правил должны начинаться разными символами,   для каждого нетерминала A, такого что A ==>* $ множество начальных символов не должно пересекаться  с множеством символов, следующих за A.: ПЕРВ(A)  СЛЕД(A) = $

Используя приведенное определение, выясним, является ли следующая грамматика слаборазделенной:

Г_{3. 7}  : R = {(1) <I>   a<A> ,

         (2) <I>   b ,          (3) <A>  c<I>a ,          (4) <A>  $ }.

Эта грамматика не содержит правил с одинаковой левой  частью, начинающихся одинаковыми терминалами, поэтому нужно проверить только условие (3) для правила (4). Вычисляя функции

ПЕРВ(<A>) = {c} и СЛЕД(<A>) = СЛЕД(<I>) = {a},

находим, что множество значений функции ПЕРВ(<A>) и множество значений функции СЛЕД(<A>) не имеют общих элементов. Следовательно, грамматика Г_3.7 является слаборазделенной. Проверка выполнения условия (3) для грамматики

Г_{3. 8}: R = { <I>   a<I><A> | $ ,

       <A>  a | b }

дает следующие результаты:

ПЕРВ(<I>) = {a} и СЛЕД(<I>) = ПЕРВ(<A>) = {a,b},

которые показывают, что пересечение множеств ПЕРВ(<I>) и СЛЕД(<I>) не пусто. Следовательно грамматика Г_3.8 не является  слаборазделенной.

25. Определение LL(1)-грамматики. Выделение общих частей.

LL(1) - грамматики.

Разделенные и слаборазделенные грамматики представляют собой подклассы грамматик более общего вида, которые называются LL(1) грамматиками, и которые определяются следующим образом. Определение. КС-грамматика является LL(1) грамматикой тогда и  только тогда, когда                           выполняются следующие два условия:                     1 . Для каждого нетерминала, являющегося левой  частью нескольких правил:                           <A>   1 |  2 | ... | n,                          необходимо, чтобы пересечение функций ПЕРВ(i) и ПЕРВ( j) было                          пусто для всех i =/= j.                     2 . Для каждого аннулирующего нетерминала <A>,такого что <A> ==>* $,                         необходимо, чтобы пересечение  множеств ПЕРВ(<A>) и СЛЕД(<A>) было                          пустым.

Из определения следует, что грамматики LL(1), в отличие от разделенных грамматик и слаборазделенных, могут содержать правила, начинающиеся нетерминальными символами. Проверим относится ли рассмотренная ранее грамматика Г₄₃  к классу LL(1). Для этого необходимо вначале проверить наличие одинаковых значений функций ПЕРВ для правил с одинаковой левой частью. Для правил (1) и (2) имеем  

ПЕРВ(<B><C>a) = ПЕРВ(<B>)  ПЕРВ(<C>) = {a,b,d,c}, ПЕРВ(g<D><B>) = {g},

а для правил (5) и (6) имеем  

ПЕРВ(<D>a<B>) = ПЕРВ(<D>)  ПЕРВ(a<B>) = {a,d}, ПЕРВ(ca) = {c}.

Полученные результаты показывают, что первое условие LL(1) грамматики выполняется. Второе условие необходимо проверить для правил (3) и (7) рассматриваемой грамматики. Вычисляя функции ПЕРВ и СЛЕД для правила (8), имеем:

ПЕРВ(<B>) = {b} и СЛЕД(<B>) = {a,c,d,g,f}.

Эти функции не имеют одинаковых значений, следовательно грамматика Г₄₃ является грамматикой LL(1). Рассматриваемый класс грамматик можно определить также с помощью множеств выбора следующим образом:

Определение. КС-грамматика называется LL(1) грамматикой тогда  и только тогда,  когда множества ВЫБОР, построенные  для правил с одинаковой левой                          частью, не содержат одинаковых элементов.

Выделение общих частей. 

Второй вид преобразований, который называют выделением общих частей, применяют для устранения правил с одинаковыми левыми частями, правые части которых  начинаются одинаковыми последовательностями символов. Например, рассмотрим грамматику с правилами

<I>   a<I>, <I>   a.

Эта грамматика не является LL(1) грамматикой, т.к. значения функций ПЕРВ(a<I>) и ПЕРВ(a) совпадают. Введем дополнительный нетерминал A и преобразуем грамматику так:

<I>   a<A>, <A>  <I>|$.

В этой грамматике отсутствуют правила с одинаковой левой частью, поэтому для нее выполняется первое условие определения LL(1) грамматики. В общем случае, если заданная грамматика содержит правила

<A>    µ₁ |  µ₂ | ... |  µ_n ,

то, вводя дополнительный нетерминал <A'>, их можно преобразовать к виду:

<A>    <A'> <A'>   µ₁ | µ₂ | ... | µ_n.

Полученные правила могут быть использованы для построения LL(1) грамматики. Покажем возможность применения этого вида преобразования на следующем примере. Пусть дана грамматика .

Г_{3. 9}:    R = { <I>   b<A><I><B>,

          <I>   b<A>,

<A>   d<I>ca, <A>   f, <B>  c<A>a, <B>   c  }.

 

Эта грамматика не является LL(1) грамматикой, поскольку нарушено первое условие. Воспользуемся способом выделения общих частей: введем нетерминалы D, E и построим правила:

<D>   <I><B> | $ <E>   <A>a | $ .

В результате включения этих правил в схему грамматики получаем:

<I>   b<A><D> <D>  <I><B> <D>  $ <A>  d<I>ca <A>  f <B>  c<E> <E>  <A>a <E>  $

Для этой грамматики первое условие принадлежности грамматики к классу LL(1) выполняется. Чтобы проверить второе условие, найдем функции ПЕРВ и СЛЕД для аннулирующих правил.

СЛЕД(<D>) = СЛЕД(<I>) = ПЕРВ(<B>)  ПЕРВ(ca) = {c}, ПЕРВ(<D>) = ПЕРВ(<I>) = {b}, СЛЕД(<E>) = СЛЕД(<B>) = СЛЕД(<D>) = {c}, ПЕРВ(<E>) = ПЕРВ(<A>) = {d,f}.

Полученные значения показывают, что второе условие выполняется, и что построенная грамматика является грамматикой типа LL(1). Преобразование для грамматики Г _{3. 9}  закончилось удачно, но так бывает не всегда. Часто исключение правил, нарушающих первое условие, приводит к появлению аннулирующих правил, для которых нарушается второе условие. Третий вид преобразования предполагает исключение аннулирующих правил и построение неукорачивающей грамматики. Такие преобразования могут оказаться полезными, если нарушается второе условие принадлежности грамматики к классу LL(1).

26. Построение детерминированного распознавателя.

Построение детерминированного нисходящего распознавателя.

Способ построения распознавателя предусматривает сопоставление каждому правилу грамматики команды распознавателя . Согласно общему способу построения распознавателей для КС-грамматик, описанному в предыдущем разделе, каждому правилу разделенной грамматики, которые имеют вид: <A>  a  , где  - цепочка символов полного словаря и a принадлежит терминальному словарю, нужно поставить в соответствие команду

(*)    f ⁰( s₀ ,  , <A> ) = ( s₀ ,  ' a) ,

которая задает такт работы без сдвига входной головки и в которой  ' представляет собой зеркальное отображение цепочки  . Отметим, что в результате выполнения этой команды, в вершине магазина окажется терминал a. Общий способ построения  редусматривает также построение для каждого a символа грамматики команды:

(**)     f ( s₀ , a , a ) = ( s₀ , $ )

которая удаляет этот терминал из магазина и сдвигает входную головку. Учитывая, что в разделенной грамматике каждое правило начинается с терминального символа, и что эти терминалы не повторяются, можно сделать вывод о том , что команда (*) должна выполняться только в том случае, когда под входной головкой находится  терминал a, и после нее всегда должна выполняться команда (**). Чтобы исключить неопределенность правил вида (*) и уменьшить число тактов работы распознавателя, объединим команды вида (*) и (**) в одну команду. Построение такой команды должно выполняться следующим образом: каждому правилу разделенной грамматики <A>   a  поставим в соответствие команду

f ( s₀ , a , <A>) = ( s₀ ,  ') ,

которая определяет такт работы распознавателя со сдвигом входной головки. Кроме того, следует учесть, что терминальные символы могут быть расположены в правых частях правил не только на самой левой позиции. Для таких терминалов необходимо построить команды вида :  

f ( s₀ , b , b ) = ( s₀ , $ )

Для перехода в заключительное состояние добавим правило:   f ( s₀ , $ ,h₀ ) = ( s₁ , $ ) ,

а в качестве начальной конфигурации распознавателя примем, как обычно, следующее выражение :   ( s₀ ,  , h₀<I> ) ,

где <I> - начальный символ грамматики, а   - заданная входная цепочка.

Применяя приведенные выше правила, построим распознаватель для разделенной грамматики Г_{3. 4} . В результате получаем:

 М _3.1 :           P = { a , b },  H = { a , b ,<I> , <B> , h₀ }, S = {s₀}, F= {s₀},

f ( s₀ , a , <I>) = ( s₀ , <B>b ) f ( s₀ , a , <B>) = ( s₀ , $ ) f ( s₀ , b , <I> ) = ( s₀ , <I> b <B> ) f ( s₀ , b , <B> ) = ( s₀ , <B> ) f ( s₀ , b , b ) = ( s₀ , $ ) f ( s₀ ,  , h₀ ) = ( s₀ , $ )

Работу построенного автомата покажем на примере анализа цепочки bbabab.   ( s₀ , bbababa , h₀<I> )  ( s₀ , bababa , h₀<I>b<B> ) 

( s₀ , ababa , h₀<I>b<B> )  ( s₀ , baba , h₀<I>b ) 

( s₀ , aba , h₀<I> )  ( s₀ , ba , h₀<B>b )  ( s₀ , a , h₀<B> )

 ( s₀ , $ , h₀ )  ( s₀ , $ , $ ) .

Приведенная последовательность конфигураций показывает, что в каждой конфигурации может быть применена единственная  команда детерминированного распознавателя.

27. Леворекурсивные правила и их недостатки. Исключение леворекурсивных правил.

Преобразование грамматик к виду LL(1). Исключение леворекурсивных правил.

Возможность построения для LL(1) грамматики детерминированного автомата определяет значение этих грамматик для практических применений. Однако, при построении грамматики для заданного языка не всегда удается получить грамматику, принадлежащую классу LL(1). Это может случиться потому, что неудачно выбраны правила грамматики, или потому, что для заданного языка принципиально нельзя построить LL(1) грамматику. В первом случае полученную грамматику можно попытаться  преобразовать таким образом, чтобы она удовлетворяла условиям LL(1) грамматики. Известно несколько приемов преобразований, которые в некоторых случаях, но не всегда, позволяют получить грамматику требуемого вида. Первый вид преобразований заключается в исключении правил, содержащих левую рекурсию. Необходимость исключения таких  правил можно показать с помощью следующих рассуждений.

• Допустим, что в схеме заданной грамматики имеются правила: <A>   <B> | <A><B>. Первое условие определения LL(1) грамматики говорит о том, что функции ПЕРВ для правил с одинаковой левой частью не должны иметь одинаковых элементов, но для заданной грамматики это не так, поскольку

ПЕРВ(<A><B>) = ПЕРВ(<A>) = ПЕРВ(<B>).

Следовательно, грамматика, содержащая рассматриваемые правила, не является LL(1) грамматикой.

• Возьмем другие правила, обеспечивающие получение такого же множества цепочек, что и в первом случае : <A>   <A><B> | $. Первое условие выполняется, но имеем: СЛЕД ( <A> ) = ПЕРВ (<B>) и ПЕРВ (<A>) = ПЕРВ (<B>), поскольку A можно заменить $. Эти равенства показывают, что нарушается второе условие из определения LL(1) грамматики. Из приведенных рассуждений можно сделать вывод о том, что LL(1) грамматика не должна содержать леворекурсивных правил. Конечно, лучше не использовать леворекурсивные правила еще на этапе построения грамматики, но если уж они появились, то их можно исключить, пользуясь приемом, описанным в предыдущем разделе.

28. Перевод. Способы описания перевода.

Описание перевода или трансляции . В общем случае перевод или трансляцию можно представить как соответствие между словами алфавита Р и алфавита W. Если цепочка   P* , цепочка   W* , они называются соответственно входной и выходной цепочками.

Определение. Если заданы входной алфавит P и выходной алфавит W, то переводом с языка Lвх, состоящего из цепочек множества P*, на язык Lвых, состоящий из цепочек множества W*, называется множество C пар цепочек ( , ) таких, что   Lвх и   Lвых. C={( , ) |   Lвх и   Lвых}.

Если входной и выходной алфавиты заданы в виде: P = {a,b,c,d} и W = {00,01,10,11}, и если входной и выходной языки содержат цепочки длиной l < 3, то соответствие между входными и выходными цепочками может быть описано, например, в виде перевода. С = {(a,00),(b,01),(c,10),(d,11),(ab,0001),(ac,0010), (cd,0011),(bc,0110),(bd,0111),(cd,1011) }.

Конечные переводы с небольшим числом элементов можно задавать в виде перечислений. Однако, для задания больших конечных переводов и бесконечных переводов нужны такие же средства задания как и для формальных языков. Рассмотрим случай , когда множество входных цепочек (входной язык перевода С) можно задать с помощью грамматики Г и множества выходных цепочек (выходной язык перевода С) - с помощью грамматики Г'. Примером такого задания может служить перевод, определяющий для каждой входной цепочки  ее зеркальное отображение  ". Если входной и выходной алфавиты состоят из двух символов - {0,1}, то правила построения такого перевода имеют вид: входные цепочки выходные цепочеки

1) <I> ╝0<I>, <I> ╝<I>0 2) <I> ╝1<I>, <I> ╝<I>1 3) <I> ╝$, <I> ╝$ Применяя одновременно соответствующие правила построения к входной и выходной цепочкам, получаем:

(<I>,<I>) ==> (0<I>,<I>0) ==> (00<I>,<I>00) ==> (001<I>,<I>100) ==> (001,100)

При таком построении существенное значение имеет заданное соответствие между правилами построения входных и выходных цепочек.

29. СУ-схемы. Перевод, определяемый СУ-схемой.

Обобщением рассматриваемого способа задания перевода с помощью двух грамматик является понятие СУ - схемы, которое может быть определено следующим образом.

Определение. Схемой синтаксически управляемого перевода (СУ-схемой) называется совокупность пяти объектов: T = {Va,Vтвх,Vтвых,Q,<I>}, где Va - множество нетерминальных символов, Vтвх- множество терминальных символов, используемых для построения входных цепочек, Vтвых- множество терминальных символов, используемых для построения выходных цепочек, <I>-начальный символ, <I>  Va, Q - множество правил вида <A> ╝ ,, где <A> принадлежит Va,  (Va U Vтвх)*,   (Va U Vтвых)* и нетерминалы, входящие в цепочку  образуют перестановку нетерминалов цепочки  .

Из приведенного определения следует, что каждое правило СУ- схемы должно включать цепочку, построенную из символов входного алфавита и нетерминальных символов, и цепочку, построенную из символов выходного алфавита и нетерминальных символов, и что в эти цепочки должны входить одни и те же нетерминалы. То обстоятельство, что основой СУ - схемы являются две грамматики, устанавливается следующим определением:

Определение. Если T = {Va,Vтвх,Vтвых,Q,I} СУ-схема, то грамматика Г = {Va,Vтвх,R, I}, где R = {<A> ╝ |<A> ╝ , принадлежит Q}, называется входной грамматикой СУ-схемы Т, а грамматика Г'={Va,Vтвых,R',I}, где R' = {<A> ╝ | <A> ╝ , принадлежит Q} называется выходной грамматикой СУ-схемы Т.

С помощью СУ - схемы можно строить пары соответствующих цепочек. Такое построение называется выводом СУ -схемы, а получаемые пары цепочек - выводимыми парами.

Определение. Парой, выводимой с помощью заданной СУ-схемы, называют любую пару, которая может быть построена с применением следующих правил: 1) (<I>,<I>) - выводимая пара, 2) если ( <A> , '<A> ') - выводимая пара и выделенные нетерминалы соответствуют друг другу и в Q существует правило <A>╝ , ', то (  ,  ' ' ') является выводимой парой.

Это записывается так: ( <A> , '<A> ') ==> (  , ' ' ').

Последовательность выводимых пар обозначим как прежде:

( <A> , '<A> ') ==>* (  , ' ' ').

Перевод, определяемый СУ-схемой.

С помощью понятия выводимая пара можно определить перевод, задаваемый СУ - схемой.

Определение. Переводом С(T), определяемым СУ-схемой Т назовем множество пар, состоящих из входной и выходной цепочек, выводимых из пары, включающей два начальных символа.  С(T) = {( , ) | (<I>,<I>) ==>* ( , ) и  Vтвх*,   Vтвых*}

В качестве примера рассмотрим СУ-схему, заданную следующим образом:

 T_4.1: V_a = {<I>,<A>}, V_твх = {0,1},V_твых = {a,b} Q = { <I> ╝0<A><I>, <I><A>a; <A> ╝0<I><A>, <A><I>a; <I> ╝1, b; <A> ╝1, b }. Эта схема определяет перевод, входные слова которого состоят из нулей и единиц, а выходные из букв а,b. Нулям входной цепочки должны соответствовать буквы a, а единицам - буквы b выходной цепочки, причем расположение символов в выходной цепочке должно быть зеркальным по отношению к соответствующим символам входной цепочки. Вывод в рассматриваемой СУ - схеме может, например, иметь вид: (<I>,<I>) ==> (0<A><I>,<I><A>a) ==> (0<A>0<A><I>,<I><A>a<A>a) ==>(0<A>00<I><A><I>, <I><A><I>aa<A>a) ==> * ==> * (0100111,bbbaaba)

30. Простая СУ-схема. Построение простой СУ-схемы.

Построение простой СУ - схемы.

В общем случае построение СУ - схемы для заданного перевода представляется более сложной задачей, чем построение двух грамматик, поскольку при этом необходимо учитывать связь или соответствие между этими грамматиками. Однако, для простых СУ - схем задача построения оказывается проще, благодаря тому, что расположение нетерминалов во входной и выходной цепочках правил должно быть одинаковым. Построение простой СУ - схемы целесообразно начинать с построения грамматики, определяющей входной язык. Такая грамматика должна быть входной грамматикой искомой СУ - схемы. Построение выходной грамматики можно совместить с построением правил СУ - схемы. Учитывая, что нетерминалы входной цепочки должны повторяться в выходной цепочке в том же порядке, перенесем все нетерминалы из входной цепочки в выходную и расставим в ней выходные терминальные символы. При этом правила, состоящие только из нетерминалов, оказываются одинаковыми во входной и выходной грамматиках. В качестве примера рассмотрим построение перевода арифметических выражений, задаваемых следующей грамматикой, в постфиксные польские выражения.

Г_{4. 1}: V_т = {x,+,(.)} V_a = {A,B.C}

R = {<A> ╝ x, <A> ╝ (<B>), <B> ╝ <A><C>, <C> ╝ +<A><C>, <C> ╝ $ }

Учитывая, что выходные выражения не должны содержать скобок, находим, что V_твых = {x',+'}. Первое правило грамматики содержит один входной терминал, поэтому правило СУ - схемы можем записать в виде: <A> ╝ x , x' .

Третье правило грамматики не содержит терминалов, поэтому получаем: <B> ╝ <A><C>,<A><C> .

Пятое правило является аннулирующим, поэтому оно должно сохраниться в выходной грамматике<C>╝$,$.

Второе правило грамматики содержит скобки, которые, согласно правилам построения, должны отсутствовать в постфиксной польской записи, поэтому имеем: <A> ╝ (<B>),<B> . При построении правила СУ - схемы по четвертому правилу грамматики следует учесть, что знак сложения в постфиксной записи должен следовать за вторым опреандом, который вводится в выражение нетерминалом А, следовательно получаем правило СУ - схемы в виде: <A> ╝ +<A><C>, <A>+'<C> .

Объединяя построенные правила, находим множество правил искомой СУ - схемы:

Т_4.4: Q = {<A> ╝ x,x', <A> ╝ (<B>),<B>, <B> ╝ <A><C>, <A><C>, <C> ╝ +<A><C>, <A>+'<C>, <C> ╝ $, $}.

Чтобы в первом приближении убедиться в правильности построения СУ - схемы, выполним вывод входной цепочки ((x+x)+x) и соответствующей ей выходной цепочки, используя построенные правила.

(<A>,<A>) ==> ((<B>),<B>) ==> ((<A><C>),<A><C>) ==> (((<B>)<C>,<B><C>) ==>

(((<A><C>)<C>),<A><C><C>) ==>(((x<C>)<C>),x<C><C>) ==> (((x+<A><C>),x'x'+'<C><C>) ==>

(((x+x+<C>)<C>), x'x'+'<C><C>) ==> (((x+x)<C>),x'x'+'<C>) ==> (((x+x)+<A><C>),x'x'+'<A>+'<C>)

==> (((x+x)+x<C>),x'x'+'x'+'<C>) ==> (((x+x)+x),x'x'+'x'+').

Полученный результат показывает, что постфиксная запись для рассматриваемой входной цепочки построена правильно.

31. Транслирующие грамматики. Входная и выходная грамматики.

Транслирующие грамматики. Основой построения СУ -схем перевода является использование двух грамматик, с помощью которых осуществляется синхронный вывод входной и выходной цепочек. Построение транслирующих грамматик предполагает применение другого подхода, который предусматривает использование одной грамматики и разрешает включение как входных, так и выходных символов в каждое правило такой грамматики.

Определение. Транслирующей грамматикой (Т -грамматикой) называется КС-грамматика, множество терминальных символов которой разбито на множество входных символов и множество выходных символов, которые называются также символами действия.

Примером Т - грамматики может служить следующая грамматика: Г_4.1: V_твх = {a,b,c}, V_твых = {x,y,z}, V_a = { I,A} R = {<I> ╝a<I>x<A>, <I> ╝z, <A> ╝<A><C>, <A> ╝by }.

Чтобы не возникало путаницы в случае использования одинаковых символов во входном и выходном алфавитах, условимся выделять выходные символы фигурными скобками. С использованием таких обозначений правила грамматики Г_Т4.1 имеют вид: R = {<I>╝a<I>{x}<A>, <I>╝{z}, <A>╝<A>c, <A>╝b{y} }.

Вывод в транслирующих грамматиках выполняется по тем же правилам, что и в обычных КС - грамматиках. Например, в рассматриваемой грамматике из начального символа может быть выведена следующая цепочка: <I> ==> a<I>{x}<A> ==> a{z}{x}<A> ==> a{z}{x]b{y}

Каждый символ или цепочка символов, заключенные в фигурные скобки, должны рассматриваться как единый символ, называемый символом действия. В общем случае цепочки символов, заключенные в фигурные скобки, можно интерпретировать как имена процедур, выполнение которых производит требуемый эффект на выходе. При описании перевода обычно предусматривают, что каждый символ действия представляет собой процедуру, осуществляющую передачу символа, заключенного в фигурные скобки, на выход. Когда нужно подчеркнуть, что используется такая интерпретация символов действия, то Т - грамматику называют грамматикой цепочного перевода.

Входная и выходная грамматики заданной транслирующей граммагики.

Из каждой Т - грамматики можно получить две обычных грамматики, одна из которых позволяет строить входные цепочки, а другая - выходные. Правила построения таких грамматик можно сформулировать следующим образом.

Определение. Если из правил транслирующей грамматики ГТ удалить выходные символы, то получим входную грамматику ГТвх для заданной грамматики. Если из правил заданной транслирующей грамматики удалить входные символы, то получим выходную грамматику ГТвых заданной транслирующей грамматики ГТ. Язык, порождаемый грамматикой ГТвх, называется входным языком заданной транслирующей грамматики, а язык, порождаемый ГТвых , называется выходным языком заданной транслирующей грамматики ГТ.

Цепочки символов, получаемые путем вывода в Т - грамматике, содержат как символы входного алфавита, так и символы выходного алфавита - символы действия. Каждую такую цепочку можно представить как пару, состоящую из входной и выходной цепочки.

Определение. Если из цепочки символов  , полученной путем вывода в заданной Т -грамматике , исключим все выходные символы, то получим цепочку 1, которую назовем входной цепочкой. Если же из цепочки  исключим все символы входного алфавита, то в результате получим цепочку 2, которую назовем выходной цепочкой, порождаемой Т - грамматикой . Цепочки 1 и 2 образуют пару, выводимую в заданной Т - грамматике.

32. Построение транслирующей грамматики.

Построение транслирующей грамматики по СУ - схеме.

Определение. Множество пар цепочек, выводимых с помощью правил заданной Т - грамматики, образуют перевод, определяемый этой грамматикой.

Последнее определение позволяет нам сделать вывод, что один и тот же перевод может быть задан как с помощью СУ - схемы, так и с помощью Т - грамматики. Эти два способа задания являются равноправными и, более того, они допускают преобразование друг в друга. Возможность одного из таких преобразований устанавливается следующим утверждением.

Утверждение. Для каждой простой СУ-схемы Т можно построить транслирующую грамматику ГТ такую, что переводы, порождаемые СУ - схемой и Т - грамматикой, совпадают. C(T) = C(ГТ)

Чтобы показать справедливость этого утверждения, опишем способ построения Т - грамматики по заданной СУ - схеме. Допустим, что задана СУ - схема Т = {V_твх, V_твых,V_a,Q,I}и требуется построить Т - грамматику

Г~ = {V'_твх,V'_твых,V'_a,R,I}. Для того чтобы получить тот же самый перевод, необходимо, чтобы V_твх = V_твх', V_твых = V_твх', V_a = V_a'. Рассмотрим преобразование правила из множества Q СУ - схемы A╝ , , где цепочки  = x_оA_ох₁А₁...x_nA_n и  = y_оA_оу₁A₁...у_nA_n, и поставим в соответствие этому правилу правило грамматики в виде: А ╝x_оу_оA_ох₁у₁A₁...x_ny_nA_n. Это можно сделать всегда, поскольку СУ - схема - простая и в каждом ее правиле используются одни и те же нетерминалы в одном и том же порядке. Рассмотренное построение обеспечивает включение во входную цепочку выходных символов цепочки, порождаемой СУ-схемой. Следовательно, каждый шаг вывода в Т - грамматике будет добавлять к выводимой цепочке те же символы, что и СУ - схема добавляет к выходной цепочке. Применение описанных положений рассмотрим на примере построения Т - грамматики по СУ - схеме Т_4.4. Используя фигурные скобки для представления выходных символов и выполняя пре-образование, получаем грамматику Г_4.1: R = {<A> ╝ x{x}, <A> ╝ (<B>), <B> ╝ <A><C>, <C> ╝ +<A>{+}<C>, <C> ╝ $ }.

Перевод цепочки ((x+x)+x) с применением правил построенной грамматики может быть получен с помощью следующего вывода: <A> ==> <A><C> ==> (<B>)<C> ==> (<A><C>)<C> ==> ((<B>)<C>)<C> ==> ((<A><C>)<C>)<C> ==> ((x{x}<C>)<C> ==> ((x{x}+<A>{+}<C>)<C>)<C> ==> ((x{x}+x{x}{+}<C>)<C>)<C> ==>((x{x}+x{x}{+})<C>)<C> ==> ((x{x}+x{x}{+})+<A>{+}<C>)<C> ==> ((x{x}+x{x}{+})+x{x}{+}<C>)<C> ==> ((x{x}+x{x}{+})+x{x}{+})<C> ==> ((x{x}+x{x}{+})+x{x}{+}).

Исключая из полученной цепочки вначале выходные, а затем входные символы, получаем выводимую пару ((x+x)+x,{x}{x}{+}{x}{+}),

которая совпадает с результатом вывода в заданной СУ - схеме.

33. Префиксная и постфиксная польские записи. Назначение.

Обычные арифметические выражения, используемые в повседневной практике и содержащие скобки называют инфиксными выражениями, поскольку знак операции располагается между операндами. Порядок выполнения действий в таких выражениях определяется старшинством опреаций и скобками. Вычисление и компиляция таких выражений подразумевает их предварительный анализ с целью выявления порядка выполнения операций. Существуют формы записи арифметических выражений без скобок, в которых порядок действий задается порядком знаков операций в выражении. Такие формы записи называются польской или бесскобочной записью. Польская запись может быть префиксной, в которой знак операции предшествует операндам, и постфиксной, в которой знак операции следует за операндом. Вычисление и компиляция бесскобочных выражений оказывается проще, чем выражений со скобками, поскольку операции должны выполняться в порядке описания и предварительный анализ не требуется.

4.3.1. Префиксная  польская  запись.  

Определение.       Префиксную польскую запись (ПрПЗ) определим так:   1) Если инфиксное выражение Е представляет собой  один операнд а, то  ПрПЗ выражение Е - это просто а.   2) Если инфиксное выражение Е1*Е2, где * - знак операции,а Е1 и Е2 инфиксные выражения для операндов,  то ПрПЗ этого выражения - это *Е1'E2',где E1', E2' - ПрПЗ  выражений Е1 и Е2.    3) Если (Е) есть инфиксное выражение, то ПрПЗ этого  выражения есть                                    ПрПЗ Е.

Это определение определяет порядок построения ПрПЗ заданного инфиксного выражения. Например для выражений (a + b) * (c - d) построение ПрПЗ можно выполнить так. Обозначим операнды первой выполняемой операции:  

    E₁ = (a + b)    и    E₂ = (c - d).

Согласно определению префиксная запись выражения Е₁*Е₂ - это *E₁'E₂', где Е₁',Е₂' -префиксные записи выражений Е₁ и Е₂. Выполняя построение постфиксных записей для этих выражений,  

        E₁' = +ab,    E₂' = -cd,

окончательно получаем результат в виде :  

*+ab-cd

4.3.2.  Вычисление  префиксных польских записей.

Вычисление ПрПЗ можно представить следующим образом:   1. Просматриваем выражение слева направо, пока не найдем знак операции, за которым       следуют два операнда.   2. Выполняем операцию и результат записываем на место выбранной тройки.   3. Повторяем пункт (1), пока не получим вместо выражения один  результат.  Вычисление построчного префиксного выражения можно  представить в следующем виде:

1. *+ab-cd 2. *R₁-cd 3. *R₁R₂ 4. R₃

       Приведенные правила вычисления префиксных записей достаточно  просты, однако, вычисление таких выражений на практике  реализуется обычно с использованием магазина. Вычисление ПрПЗ с использованием магазина выполняется следующим образом.

1. Прочитать очередной символ входной цепочки.

2. Если входной символ - оператор, то занести его в магазин     безусловно.

3. Если входной символ - операнд, то выполняемые действия     зависят от того какой символ находится в вершине магазина:  

a) Если в вершине находится оператор, то выполнить     запись в магазин.

б) Если в вершине находится операнд, то выполнить     чтение операнда и следующего за ним оператора,     а затем выполнить операцию и повторить п.3 - проверку     символа в вершине магазина.  

4. Повторить п.1 пока не будут прочитаны все символы     входной цепочки.

Порядок вычислений префиксных выражений покажем на примере входной цепочки *+ab-cd в виде следующей схемы:

        Вход                  Магазин                       Операция

1.    *+ab-cd                 h_о

2.    +ab-cd                   h_о*

3.     ab-cd                    h_о*+

4.     b-cd                      h_о*+a

5.    -cd                         h_о*R₁                               a+b=R₁

6.     cd                         h_о*R₁-

7.     d                           h_о*R₁-c

8.     $                           h_о*R₁                       c-d=R₂, R₁*R₂=R₃

                                     h_оR₃   4.3.3.  Постфиксная  польская запись.

Определение. Постфиксную польскую запись (ПоПЗ) определим так:       1. Если инфиксное выражение Е представляет собой один  операнд а, то ПоПЗ  выражения Е - это а.       2. Если инфиксное выражение Е1*Е2, где * - знак операции,  E1, E2 - инфиксные выражения для операндов, то ПоПЗ  этого выражения это - Е1'E2'*, где Е1',E2' -  постфиксные  выражения Е1,Е2.      3. Если (Е) есть инфиксное выражение, то постфиксная   запись этого выражения  есть постфиксная запись Е.

Аналогично предыдущему примеру построим ПоПЗ выражения

(a + b) * (c - d).

Обозначая операнды внешней операции

E₁ = (a + b)  и E₂ = (c - d),

найдем постфиксные записи операндов, которые имеют вид:

E₁' = ab+ и E₂' = cd-.

Подставляя полученные постфиксные записи в выражение

E₁'E₂'*,

окончательно получаем :

ab+cd-* .

 4.3.4.   Вычисление постфиксных польских записей

Вычисление постфиксной записи выражения можно представить следующим образом. 1. Просматриваем выражение слева направо пока не найдем два стоящих рядом операнда, за     которыми  следует знак операции. 2. Выполняем операцию и записываем результат вместо  выбранных операндов и операций. 3. Повторяем пункт (1) пока не получим вместо выражения  единственный результат. Вычисление построенного постфиксного выражения можно представить в следующем виде:

1. ab+cd-*

2. R₁cd-*

3. R₁R₂*

4. R₃

На практике вычисление постфиксных выражений реализуется с применением магазина. В этом случае вычисления выполняются по следующим правилам. 1. Прочитать очередной символ входной цепочки. 2. Если входной символ - операнд, то выполнить его запись   в магазин. 3. Если входной символ - оператор,то прочитать два операнда  из магазина, выполнить     операцию и результат занести в магазин   как операнд. 4. Повторять п.1, пока во входной цепочке не будут прочитаны  все символы. Последовательность вычислений продемонстрируем на примере входной цепочки                                                             ab+cd-* и изобразим ее в виде следующей схемы:  

         Вход                 Магазин                    Операция

        ab+cd-* 1.     b+cd-*                    a 2.     +cd-*                      ab 3.     cd-*                        R₁                             a+b=R₁ 4.     d-*                          R₁c 5.     -*                            R₁cd 6.      *                            R₁R₂                        c-d  = R₂ 7.      $                            R₃                          R₁*R₂ = R₃

4.3.5.  Примеры  постфиксных  польских записей.

Польские постфиксные записи часто используют в качестве промежуточного представления операторов языков программаирования на этапе синтаксического анализа при компиляции. В качестве примеров такого применения приведем постфиксные выражения для некоторых операторов Паскаля. Знак присваивания можно рассматривать как символ операции, поэтому оператор присваивания:

<I> := <E>,

где I-идентификатор, а Е- арифметическое выражение, можно записать в виде постфиксного выражения

<I><E>':= ,

где  E'- постфиксная запись выражения Е . Для описания построения записи конструкции с условием требуется введение новых элементов: метки и операторов условного и безусловного переходов. Условимся для обозначения меток в постфиксных выражениях использовать идентификаторы М,М₁,М₂,...,а для обозначения переходов воспользуемся операторами Условный Переход по значению Ложь (УПЛ) и Безусловный Переход (БП). Операндами этих операторов являются метки. Первый оператор выполняет переход к метке, если значение выражения, предшествующего этому оператору, ложно. Если же значение выражения, предшествующего оператору УПЛ, истинно, то оператор пропускается и выполняется оператор, расположенный непосредственно за УПЛ. Результатом оператора безусловного перехода с меткой М является то, что следующим выполняется оператор из рассматриваемой последовательности, помеченный М. Для постфиксного представления простого условного оператора   IF <R> THEN <S> ,

где <R> - отношение, а <S> - оператор , воспользуемся условным оператором перехода. В результате получаем выражение:   <R'>M УПЛ <S'>M ,

в котором <R'> и <S'> являются постфиксными выражениями соответствующего выражения и оператора, а М - метка. Опреатор <S'> в этом выражении также как и в заданном условном операторе выполняется только в том случае, когда отношение <R'> - истино. Для полного условного оператора    IF <R> THEN <S₁>ELSE <S₂>,

где<R> - отношение, а <S₁>,<S₂ >- операторы, постфиксное представление должно обеспечивать выполнение одного из операторов <S₁>или <S₂>в зависимости от условия <R>. Исходя из этого положения, постфиксную форму полного условного оператора можно записать так:   <R'> M₁ УПЛ <S₁'> M₂ БП М₁ <S₂'> M₂ ,

где <R'> - постфиксная запись отношения <R>, <S₁'> и <S₂'>- постфиксные записи операторов <S₁>,<S₂>, а М₁ и М₂ - метки.

  34. Магазинный преобразователь. Структура. Определение.

Магазинные Преобразователи.

Магазинные автоматы, рассмотренные в предыдущем разделе, позволяют определить для цепочки, заданной на входе, ее принадлежность к языку, допускаемому автоматом. Настоящий раздел посвящен другому типу моделей устройств, называемому магазинными преобразователями. Подобные устройства позваляют строить по заданной входной цепочки соответствующую ей выходную цепочку. Множество таких пар цепочек называют переводом или трансляцией, допускаемым магазинным преобразователем. Для того чтобы построить преобразователь необходимо заранее знать какой перевод он должен выполнять. Кроме того, преобразователь можно построить не для любого перевода, а только для такого, который может быть описан с помощью простой СУ-схемы. Для построения детерминированного преобразователя необходимо еще, чтобы входная грамматика заданной СУ-схемы пораждала детерминированный язык.

Магазинный преобразователь (Мп) от магазинного автомата наличием дополнительной выходной ленты, на которую записывается выходная цепочка. Схему магазинного преобразователя можно изобразить следующим образом:

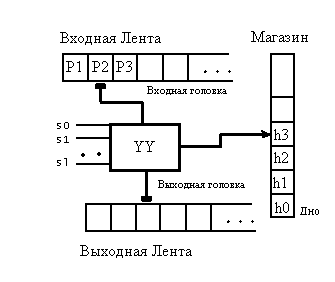
В этой схеме входная головка в каждом такте работы может оставаться на месте или двигаться на одну позицию вправо. Выходная головка также может быть неподвижной или смещаться вправо, а головка магазинной ленты может перемещаться в обоих направлениях, причем такие перемещения связаны с операциями записи и чтения. Описание работы магазинного преобразователя.

Для описания работы магазинного преобразователя необходимо дать его определение.

Определение: Преобразователем с магазинной памятью (Мп) называется совокупность восьми объектов: Мп={P, S, s0, H, h0, F, W, q}, где P - входной алфавит, состоящий из символов, записываемых на входную ленту;  W - выходной алфавит, содержащий символы, записываемые на выходную ленту;  H - магазинный алфавит, содержащий символы, записываемые и считываемые из магазина; h0 - маркер дна магазина, он принадлежит H; S - множество состояний преобразователя; s0- начальное состояние из множества S; F - множество конечных состояний, представляющих собой подмножество S;  - функция переходов преобразователя, которая задает отображение, : Sx{P  {$} x H  S x H* x W* . Она может быть записана в функциональном виде: (s, p, h) = (s', , ),  где h  H, p  P,   H*,   W* и s,s'  S.

Определим конфигурацию Мп как четверку

(s, a, h, ),где a  P*, h  H* и   W*. Если такту работы преобразователя соответствует конфигурация (s, a, h , ) и определена функция переходов (s, a, h) = (s', , ), то происходит смена конфигурации, которую условимся записывать так: (s, a, h, ) |-- (s', , , ).

Последовательность сменяющих друг друга конфигураций, как обычно, обозначим символом |--*. В качестве начальной примем конфигурацию, которой соответствует заданная входная цепочка  на ленте, цепочка h₀I в магазине, начальное состояние s₀ и пустая цепочка на выходной ленте: (s₀, , h₀I, $). Конечной или заключительной конфигурацией назовем четверку (s_k, $, $, ), где s_k - одно из заключительных состояний из множества F, а  - выходная цепочка.

35. Описание работы магазинного преобразователя.

  Магазинный преобразователь (Мп) от магазинного автомата наличием дополнительной выходной ленты, на которую записывается выходная цепочка. Схему магазинного преобразователя можно изобразить следующим образом:

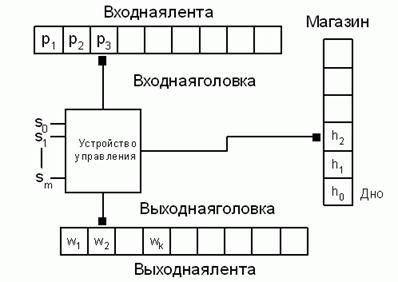
    В этой схеме входная головка в каждом такте работы может оставаться на месте или двигаться на одну позицию вправо. Выходная головка также может быть неподвижной или смещаться вправо, а головка магазинной ленты может перемещаться в обоих направлениях, причем такие перемещения связаны с операциями записи и чтения.

4.7.2. Описание работы магазинного преобразователя.

    Для описания работы магазинного преобразователя необходимо дать его определение.

 

Определение: Преобразователем с магазинной памятью (Мп) называется совокупность восьми                               объектов:  Мп={P, S, s0, H, h0, F, W, q},        где P - входной алфавит, состоящий из символов, записываемых на входную ленту;      W - выходной алфавит, содержащий символы, записываемые на выходную ленту;          H - магазинный алфавит, содержащий символы, записываемые и считываемые из     магазина;  h0 - маркер дна магазина, он принадлежит H;  S - множество состояний преобразователя;  s0- начальное состояние из множества S;  F - множество конечных состояний, представляющих собой подмножество S;   - функция переходов преобразователя, которая задает отображение,  : Sx{P  {$} x H  S x H* x W* . Она может быть записана в функциональном виде:   (s, p, h) = (s', , ),  где h  H,  p  P,    H*,   W* и s,s'  S.

Определим конфигурацию Мп как четверку

(s, a, h, ), где a  P*, h  H* и   W*. Если такту работы преобразователя соответствует конфигурация (s, a, h , ) и определена функция переходов (s, a, h) = (s', , ), то происходит смена конфигурации, которую условимся записывать так:

(s, a, h, ) |-- (s', , , ).

Последовательность сменяющих друг друга конфигураций, как обычно, обозначим символом |--*. В качестве начальной примем конфигурацию, которой соответствует заданная входная цепочка  на ленте, цепочка h₀I в магазине, начальное состояние s₀ и пустая цепочка на выходной ленте: (s₀, , h₀I, $).     Конечной или заключительной конфигурацией назовем четверку (s_k, $, $, ), где s_k - одно из заключительных состояний из множества F, а  - выходная цепочка.

4.7.3.  Перевод определяемый преобразователем.

Определение.  Цепочку назовем выходом для цепочки , если существует последовательность  конфигураций, первой из которых является начальная конфигурация с заданной   входной цепочкой , а последней – заключительная конфигурация с выходной  цепочкой :                                     (s0, , h0I, $) |--* (s', $', $, ). Определение.  Переводом, определяемым преобразователем с магазинной памятью Мп,  назовем множество пар, состоящих из входных и соответствующих им  выходных цепочек.  D(Mп) = {(x, y) | (s0, , h0, $) |--* (s', $', $, y) & s' F}

   Используя последнее определение, можно определить возможность построения преобразователя, реализующего заданный перевод в виде следующего утверждения.

Утверждение.   Для каждой простой СУ-схемы перевода Т = {Va, Vтвх, Vтвых, Q, I} можно   построить такой Мп магазинный преобразователь, что D(Т) = D(Мп).

    Приведенное утверждение говорит о возможности построения преобразователя, но не гарантирует получение детерминированного преобразователя, который может быть получен при выполнении следующих условий: 

Утверждение.  Для каждой простой СУ - схемы перевода Т, входная грамматика которой  принадлежит классу LL(1) - грамматик, можно построить такой  детерминированный магазинный  преобразовательМп, что перевод,  оеделяемый преобразователем, совпадает  с переводом, задаваемым   СУ - схемой Т

36. Детерминированный преобразователь. Построение магазинного преобразователя.

Утверждение.  Для каждой простой СУ - схемы перевода Т, входная грамматика которой  принадлежит классу LL(1) - грамматик, можно построить такой  детерминированный магазинный  преобразовательМп, что перевод,  оеделяемый преобразователем, совпадает  с переводом, задаваемым   СУ - схемой Т . 

Построение преобразователя.

Покажем теперь, как по заданной СУ - схеме можно построить детерминированный преобразователь. В начале по заданной СУ - схеме построим транслирующую грамматику Г. Это всегда можно сделать, поскольку заданная СУ - схема должна быть простой. Если входная грамматика заданной СУ - схемы относится к классу LL(1) -грамматик, то и входная грамматика транслирующей грамматики также должна относиться к этому классу, поскольку при построении Т - грамматики входные правила изменениям не подвергались. Учитывая, что искомый преобразователь должен в процессе формирования выхода осуществлять и распознавание входной цепочки, будем его строить по правилам транслирующей грамматики, используя правила построения распознавателя. Такой преобразователь должен воспроизводить левый вывод входной цепочки в магазине и удалять терминальные символы, на ходящиеся в вершине, при совпадении их с очередным символом на входной ленте. Однако при этом в магазин будут записываться выходные символы, содержащиеся в правилах Т - грамматики, и возникнут неопределенные ситуации при появлении выходного символа в вершине магазина. Чтобы исключить такие ситуации, дополним этот правила построения преобразователя следующим правилом: при появлении выходного символа в вершине магазина он должен передаваться на выход независимо от того, какой символ находится под входной головкой. Построение функции переходов МП (1) для всех правил вида <A> --> b, где b  V_твх и  (V_твх U V_твых U V_a)*, строим команды: ( s₀, b, A)=( s₀, ', $ ), где ' - зеркальное отображение цепочки . (2) Для всех правил вида <A> --> <B>, где B Va и  (V_твх U V_твых U V_a)*, строим команды: *( s₀, u, A ) = ( s₀, B , $ ), где u  ВЫБОР(<A> --> <B>_вх) и _вх - цепочка, полученная из  путем удаления из нее всех выходных символов. . (3) Для всех правил вида <A> --> $ строим команды: *( s₀, u, A ) = ( s₀, $, $ ), где u  ВЫБОР(<A> --> $). (4) Для всех символов b, принадлежащих, V_твх , стоящих на первом месте в правой части правил транслирующей грамматики, т.е. символов,заносимых в магазин, строим правило: ( s₀, b, b ) = ( s₀, $, $ ). (5) Для всех выходных символов {u}, таких что u  V_твых U {$}, строим команды: *( s₀, z, {u} ) = ( s₀, $, {u} ), где z  Vтвх. Точнее команды строятся для сочетаний {u}z, таких что z может следовать за {u} в цепочках, выводимых в за данной грамматике. (6) Заключительное правило строим так: ( s₀, $, h0 ) = ( s₀, $, $ ).

Пример построения преобразователя. Применение правил построения команд преобразователя рассмотрим на примере транслирующей грамматики Г, которая описывает перевод инфиксных выражений, состоящих из идентификаторов и знаков + и *, в постфиксные польские выражения. Эта грамматика имеет следующую схему:  Г _{4. 2} : R = {<E> +<E><E>{+}, <E> x<E><E>{x}, <E> a{a}}

Используя правило построения команд преобразователя (1) для правил грамматики, начинающихся входным терминальным символом, получаем команды преобразователя Мп1: q(s₀, +, <E>) = (s₀, {+}<E><E>, $), q(s₀, *, <E>) = (s₀, {*}<E><E>, $), q(s₀, a, <E>) = (s₀, {a}, $)

Правила построения команд вида (2),(3),(4) к заданной грамматике неприменимы, поэтому с помощью правил вида (5) построим команды, обеспечивающие передачу выходных символов на выход. Эти команды имеют вид: q*(s₀, +, {+}) = (s₀, $, +), q*(s₀, *, {+}) = (s₀, $, +), q*(s₀, a, {+}) = (s₀, $, +), q*(s₀, $', {+}) = (s₀, $, +), q*(s₀, *, {*}) = (s₀, $, *), q*(s₀, +, {*}) = (s₀, $, *), q*(s₀, *,{a}) = (s₀, $, *), q*(s₀, $',{*}) = (s₀, $, *), q*(s₀, a,{a}) = (s₀, $, a), q*(s₀, +{a}) = (s₀, $, a), q*(s₀, *,{a}) = (s₀, $, a), q*(s₀, $', {a}) = (s₀, $, a)

Для перехода в заключительное состояние s₁ в соответствии с правилом (6) построим команду:

q(s₀, $', h₀) = (s₁, $, $) Чтобы посмотреть как работает построенный преобразователь, рассмотрим построение выходной цепочки для входа +a*aa. Последовательность конфигураций, получаемых с помощью команд преобразователя имеет вид: (s₀, +a*aa, h₀E, $) |-- (s₀, a*aah₀{+}EE, $) |-- (s₀, *aa, h₀{+}T{a}, $) |-- (s₀, *aa, h₀{+}E, a) |-- (s₀, aa, h₀{+}{*}T{a}, a) |-- (s₀, a, h₀{+}{*}E, aa) |-- (s₀, $, h₀{+}{*}{a}, aa) |-- (s₀, $, h₀{+}{*}, aaa) |-- (s₀, $, h₀{+}, aaa*)|-- (s₀, $, h₀, aaa*+) |-- (s₀, $, $, aaa*+).

Результатом работы преобразователяявляется выходная цепочка aaa*+, представляющая постфиксную запись заданной входной цепочки.

37. АТ - грамматики. Определение. Назначение. 

АТ-грамматики отличаются от транслирующих грамматик тем, что символам грамматики приписываются атрибуты, отражающие семантическую информацию, а правилам грамматики сопоставляются правила вычисления значений атрибутов. Чтобы пояснить назначение атрибутов, приведем несколько примеров. Если входной язык предусматривает использование констант C, то в качестве атрибута константы можно взять ее значение. Условимся записывать значение константы за ее обозначением с разделителем в виде косой черты, например, C/5. Если в Т-грамматике используются операционные символы {сложить}, то в качестве атрибутов таких  символов можно взять значения операндов и результата. Обозначая атрибуты символами x, y, z, операционный символ с атрибутами запишем в виде {сложить}/x/y/z.

В АТ-грамматиках используются атрибуты двух видов: наследуемые и синтезируемые. Значения наследуемых атрибутов определяются при выполнении очередного шага вывода по значениям атрибутов цепочки, содержащихся в левой части правила грамматики. Вычисление значений синтезируемых атрибутов может откладываться и определяться при выполнении последующих шагов вывода. В общем  виде свойства АТ-грамматик могут быть сформулированы следующим образом.

Определение.  Транслирующую грамматику называют атрибутной грамматикой или АТ-грамматикой если: 1. Символам грамматики приписаны один или несколько атрибутов и для каждого атрибута определено множество допустимых значений. 2. Атрибуты могут быть наследуемыми и синтезируемыми. 3. Для каждого правила грамматики должны быть заданы правила вычисления атрибутов в виде оператора присваивания с функцией в правой части, определяющей значение атрибута, расположенного слева. Такие функции для вычисления атрибутов могут зависеть от атрибутов правой или левой частей рассматриваемого правила. 4. Для наследуемых атрибутов начального символа должны быть заданы начальные значения. 5. Функции, вычисляющие значения синтезируемых атрибутов символов действия, должны зависеть от других атрибутов этого символа.

Атрибутные транслирующие грамматики могут быть использованы для построения выводов, в которых построение цепочки совмещается с вычислением значений атрибутов. Чтобы различать атрибуты в правилах вывода, условимся записывать синтезируемые атрибуты с префиксом в виде знака процента (%), а наследуемые - с префиксом в виде наклонной черты (/). Например, если символ <X> имеет один синтезируемый атрибут a и два наследуемых атрибута b, c, а символы <Y> и <Z> имеют по одному наследуемому атрибуту d и e, то правило <X><Y><Z> может быть записано в виде:   <X>%a/b/c  <Y>/d<Z>/e.

    Это правило вывода необходимо дополнить правилами вычисления значений атрибутов, которые в соответствии с приведенным определением могут иметь вид:   a := b+d; d := 2*c; e := b.

    В дальнейшем правила вычисления атрибутов условимся записывать непосредственно за правилами вывода или на отдельной строчке, отделяя их от правил вывода двумя восклицательными знаками (!!).

    В качестве первого примера рассмотрим АТ-грамматику, описывающую трансляцию выражений, состоящих из констант C, в значение заданного выражения.

    Допустим, что у каждого нетерминала <E>, <T>, <P> имеется по одному атрибуту, принимающему целочисленные значения. Терминальный символ C также имеет один атрибут, определяющий значение константы и принимающий целочисленные значения. Операционный символ грамматики {ответ} имеет наследуемый атрибут с целочисленной областью значений. Начальным символом грамматики служит символ <S>. В тех случаях, когда атрибуты символов действия должны передаваться на выход вместе с этими символами действия, как это имеет место в рассматриваемом примере, условимся записывать атрибуты символов действия внутри фигурных скобок.   Г _{5. 0} :        <S> <E>%a{ответ/b}

!! b := a <E>%d <E>%e+<T>%f !! d := e+f <E>%g <T>%h !! g := h <T>%i <T>%j*<P>%k !! i := j*k <T>%m <P>%n !! m := n <P>%p (<E>%q) ! p := q <P>%r C/s !! r := s.

38. LАТ - грамматика. Назначение грамматики.

Определение.  АТ-грамматика является L - атрибутной транслирующей грамматикой, если выполняются следующие три условия:     1) Каждый наследуемый атрибут символа правой части правила грамматики должен вычисляться с использованием либо наследуемых атрибутов символов левой части правила, либо с использованием произвольных атрибутов символов правой части правила, расположенных левее данного символа.     2) Каждый синтезируемый атрибут символа левой части правила грамматики должен вычисляться с использованием наследуемых атрибутов этого символа левой части правила или произвольных атрибутов символов правой части этого правила.     3) Каждый синтезируемый атрибут символа действия должен вычисляться по наследуемым атрибутам этого символа действия.

    Значение условия 1 состоит в том, что оно обеспечивает зависимость наследуемых атрибутов от величин, находящихся только слева от них в правиле грамматики (символ L в обозначении LАТ-грамматики - это сокращение от Left - левый). Это условие позволяет обрабатывать атрибуты сверху вниз, потому что каждый символ обрабатывается до того, как прочитаны символы справа от него. Условия 2 и 3 обеспечивают исключение круговых зависимостей атрибутов. Все три условия, взятые вместе, приводят к следующему порядку вычисления атрибутов для правила вида  

<A>  <B><C>:

1) наследуемые атрибуты <A>, 2) наследуемые атрибуты <B>, 3) синтезируемые атрибуты <B>, 4) наследуемые атрибуты <C>, 5) синтезируемые атрибуты <C>, 6) синтезируемые атрибуты <A>.

    Чтобы убедиться в том, что заданная АТ-грамматика обладает свойствами LАТ-грамматики, нужно проверить для каждого правила грамматики выполнение условий 1 и 2, а также для каждого символа действия - выполнение условия 3. Такая проверка заключается в анализе зависимостей атрибутов для каждого правила их вычисления.     В качестве иллюстрации выполним анализ возможных зависимостей атрибутов, отвечающих описанным условиям, для следующего правила:  

<A>/a1%x1%y1 <B>/b1<C>%x2<D>%y2/a2/b2<E>/a3

    Анализ зависимостей этого правила должен заключаться в проверке того, что правила вычисления атрибутов b1, a2, b2, a3 должны удовлетворять условию 1, а правила вычисления атрибутов x1, y1 - условию 2. Согласно условию 1 правило вычисления атрибута b1 может использовать для вычисления только атрибут a1, поэтому такие правила могут, например, иметь вид:  

b1 = f(a1) или b1 = 112  или (b1,b2) = a1.

    Последнее из приведенных выражений обозначает множественное присваивание, когда двум величинам одновременно присваивается одно и то же значение.

Отметим также, что правила вычисления не могут иметь, например, следующий вид:  

b1 = x1 или b1 = g(y2,b1).

    Условие 1 для рассматриваемого правила позволяет использовать для вычисления атрибутов a2 и b2 в качестве аргументов величины a1, b1, x2, а при вычислении a3 аргументами могут быть a1, b1, x2, y2, a2, b2.

    Согласно условию правила 2 при вычислении атрибутов x1 и y1 могут быть использованы любые атрибуты кроме самих x1, y1.

    Условие 3 используется для проверки символов действия. Чтобы убедиться в его выполнении, нужно просмотреть список аргументов правил вычисления атрибутов и убедиться, что среди них нет синтезированных атрибутов.

39. Форма простого присваивания. Назначение грамматики.

Форма простого присваивания АТ-грамматик

    Вторым видом ограничений, накладываемых на АТ-грамматики, предназначенные для построения преобразователей, является запрещение использования в правилах вычисления атрибутов нетерминальных символов и некоторых атрибутов символов действия функциональных зависимостей. При выполнении этого запрета правила вычисления атрибутов должны иметь форму операторов присваивания с переменными в правой части. Грамматика с такими правилами называется АТ-грамматикой простого присваивания.     Чтобы сократить число правил вычисления атрибутов, в таких грамматиках разрешается использовать правила не только в виде простых операторов присваивания                                                             a = b, но и в виде операторов множественного присваивания                                                             (a1, a2, a3) = b, когда нескольким переменным присваивается одно и то же значение. Правила в виде простых и множественных операторов присваивания называются копирующими правилами. Правую часть таких правил называют источником, а каждый атрибут левой части - приемником.  

Определение. Множество копирующих правил называется независимым тогда и только тогда, когда источник каждого правила из этого множества не входит ни в одно из других правил этого множества.

Если копирующие правила являются зависимыми, то в некоторых случаях их можно объединить в одно правило. Например, правила

a = x и (b, c) = x

можно записать как одно правило

(a, b, c) = x,

или правила

(a, x) = z и (b,c) = x

также можно записать в виде

(a, b, c, x) = z,

поскольку источнику второго правила x, согласно первому правилу, присваивается значение z. Если копирующие правила являются независимыми, то их объединять нельзя. Используя понятие независимости копирующих правил, сформулируем следующее определение.

Определение. АТ-грамматика имеет форму простого присваивания, если выполняются следующие условия: а) все правила вычисления атрибутов, за исключением правила вычисления синтезируемых символов действия, являются копирующими, б) для каждого правила грамматики множество копирующих правил является независимым.

    Свойства L - атрибутности и простого присваивания АТ-грамматик являются необходимыми для построения преобразователя, реализующего атрибутный перевод.  

Утверждение: Если заданная АТ–грамматика не имеет формы простого присваивания, то для нее можно построить эквивалентную АТ-грамматику в форме простого присваивания.

Такое построение связано с исключением некопирующих правил вычисления атрибутов и добавлением вместо них операционных символов в правила грамматики.

    Прежде чем описать последовательность преобразования некопирующих правил, рассмотрим пример, иллюстрирующий как такое преобразование выполняется. Допустим, что задано некопирующее атрибутное правило в виде:  

<A>  a/x<B>%y<C>/z            !!   z = f(x, y).

    Вначале введем новый символ действия, представляющий вычисление функции f. Обозначим символ действия {f} и снабдим его тремя атрибутами. Два наследуемых атрибута b1, b2 необходимы для задания аргументов функции, и один синтезируемый атрибут с – для получения значения функции. В результате получаем следующее определение символа действия:  

{f}/b1/b2%c,

где значение с определяется как функция f(b1, b2).

    Затем включим новый символ действия в правило грамматики и заменим некопирующее правило вычисления атрибута с функцией f в правой части несколькими копирующими правилами, устанавливающими связь между атрибутами нового символа действия и аргументами функции f.  После выполнения перечисленных действий может быть получено следующее атрибутное правило:

<A> a/x<B>%y{f}/b1/b2%c<C>/z           b1 = x; b2 = y; z = c,

которое содержит только копирующие правила, два из которых копируют аргументы, и одно - результат. Это правило дает тот же эффект, что и первоначальное правило, в том смысле, что оба правила порождают одинаковые выходные цепочки с атрибутами и дают одно и то же значение атрибута z.     Необходимо подчеркнуть, что место включения нового нетерминального символа в правило грамматики должно выбираться с таким расчетом, чтобы не нарушить свойств L - атрибутности заданной грамматики. Если в рассматриваемом примере поместить новый символ действия перед нетерминалом <B>, то получим правило

<A> a/x{f}/b1/b2%c<B>%y<C>/z          b1 = x; b2 = y; z = e,

в котором значение наследуемого атрибута b2 определяется синтезируемым атрибутом y, расположенным правее него, что нарушает свойство L - атрибутности. Если же поместить новый символ действия после символа <C>, то получим правило                                        <A> a/x<B>%y<C>/z{f}/b1/b2/c                                                   b1 = x; b2 = y; z = c, в котором атрибут z определяется по атрибуту с, расположенному правее него, что также нарушает свойство L - атрибутности. Таким образом, в рассматриваемом примере оказалось, что расположить новый символ действия без нарушения свойств L - атрибутности  возможно только в одной позиции правила - между нетерминалами <B> и <C>.     В общем случае в правиле может оказаться несколько позиций, пригодных для размещения нового символа действия. Если это так, то предпочтение следует отдать самой левой из возможных позиций, поскольку в некоторых случаях самые левые символы действия не нужно заносить в магазин преобразователя, производящего обработку.     Если же оказывается, что все позиции, в которых может быть расположен новый символ действия, являются непригодными и приводят к нарушению свойств L - атрибутности, то преобразовать такую грамматику невозможно.

40. Преобразование LAT-грамматики в грамматику формы простого присваивания.

Преобразование LАТ-грамматики в LАТ-грамматику в форме простого присваивания.

    В качестве итога проведенного анализа опишем последовательность преобразования заданной LАТ-грамматики в LАТ-грамматику в форме простого присваивания.

1) Для каждой функции f(x1, x2, ..., xn), входящей в правила вычисления атрибутов, связанных с некоторым правилом грамматики, введем дополнительный символ действия с n+1 атрибутом, который обозначим {f} и определим следующим образом:

{f}/a1/a2/.../an%y,

где значение y определяется как f(a1, a2, ..., an).

2) Для каждого некопирующего правила

(z1, z2, ..., zn) = f(x1, x2, ..., xn),

связанного с некоторым правилом грамматики, включим в правую часть правила грамматики символ

{f}/a1/a2/.../an%y,

полагая, что символы a1, a2, ..., an и y не содержатся в правиле грамматики, и заменим некопирующее правило на n+1 копирующих правил вида:

ai = xi; (z1, z2, ..., zm) = y.

3) При включении символа действия {f}/a1/a2/.../an%y необходимо соблюдать следующие ограничения: а) Символ действия должен располагаться правее каждого символа правой части правила грамматики, атрибутом которого является один из аргументов x1, x2, ..., xn. б) Символ действия должен располагаться левее каждого символа правой части грамматики, атрибутом которого является один из символов z1, z2, ..., zm. в) Если существует несколько позиций для размещения символа действия, то предпочтение следует оказать самой левой из возможных позиций. 4) Два копирующих правила одного и того же правила грамматики следует объединить в одно правило, если источник одного из них входит в другое. Это объединение осуществляется путем удаления правила с лишним источником и объединения его получателя с получателями оставшегося правила. Отметим, что следует соблюдать осторожность при объединении зависимых правил, использующих в правой части процедуры без параметров, которые можно рассматривать как константы и, следовательно, считать источниками, поскольку могут возникнуть ошибки за счет того, что разные вызовы процедур могут давать разные значения. Например, правила

x = СЛЕДУК и y = СЛЕДУК

объединить нельзя, поскольку значениями x и y будут указатели на соседние элементы ТЗ. В качестве примера преобразования АТ-грамматики в грамматику в форме простого присваивания выполним такое преобразование для грамматики Г _{5. 0}. Введем для правил, содержащих операции, операционные символы {сложить} и {умножить}, приписывая каждому символу два наследуемых и один синтезируемый атрибуты. В результате получаем грамматику в форме простого присваивания:

                        Г _{5. 5} :

<S> E%a{ОТВЕТ/b} !! b=a;

<E>%d <E>%e+T%f{СЛОЖИТЬ}/x1/x2%y               !! x1 = e; x2 = f; d = y; <E>%g <T>%h              !! g = h; <T>%i <T>%j*<P>%k{УМНОЖИТЬ}/z1/z2%u              !! z1 = j; z2 = k; i = u; <T>%m <P>%n             !! m = n <P>%p  (<E>%q)           !! p = q; <P>%r c/s         !! r = s;

    Ограничения, накладываемые на атрибуты LAT–грамматиками в форме простого присваивания, делают возможным использование таких грамматик для построения атрибутных преобразователей (АТ-преобразователей). Основой построения АТ–преобразователей являются следующие соображения.     Если из правил LAT-грамматики удалить все атрибуты, то получится транслирующая грамматика, для которой может быть построен нисходящий магазинный преобразователь. Следовательно, АТ-преобразователь можно строить в виде магазинного преобразователя, дополненного действиями, связанными с обработкой атрибутов.     При определении значений синтезируемых атрибутов в LAT-грамматиках могут возникать отложенные присваивания, поэтому, планируя работу АТ-преобразователя, необходимо предусмотреть возможность сохранения атрибутов, значения которых еще не определены. Для сохранения таких атрибутов может быть использован магазин. Простое сохранение атрибутов является недостаточным, поскольку необходимо еще сохранять сведения о том, какое значение должен получить атрибут. Учитывая, что в форме простого присваивания используется только один способ определения значения - с помощью оператора присваивания, можно отобразить сведения о присваиваниях в магазине с помощью указателей. Для этого в каждый элемент магазина, соответствующий источнику, можно записать указатель на элемент, соответствующий приемнику. Такие указатели можно устанавливать в магазине при записи в него правой части правила грамматики. В этом случае должен обеспечиваться порядок определения значений атрибутов, в котором всегда вначале определяется источник, а затем приемник. Получение такого порядка вычислений гарантируют свойства L - атрибутности грамматики. Оно предусматривает, что каждое значение атрибута определяется значениями атрибутов, расположенных слева от него в правилах грамматики. Учитывая, что в магазин записывается зеркальное отображение правой части правила, можно утверждать, что атрибуты, расположенные левее рассматриваемого атрибута, будут вычисляться раньше него, обеспечивая тем самым требуемый порядок вычисления атрибутов.

41. Атрибутные преобразователи. Представление правил LAT-грамматики в магазине.