1.5.1. Рекомендации по построению грамматик

Основой создания правил грамматики является способ выделения структуры заданного множества цепочек. Этот способ предусматривает расчленение цепочек, входящих в заданное множество, на части таким образом, чтобы выявить повторяющиеся части цепочек и части, входящие во все цепочки в неизменном виде. Такое расчленение на части представляет собой выявление структуры цепочек заданного множества. Для каждого выявленного элемента структуры введем обозначения. Множество таких обозначений составляет основу словаря нетерминальных символов некоторой грамматики. Следующим шагом построения является выявление последовательностей, в которых элементы структуры могут входить в заданные цепочки. Такие последовательности являются основой для построения правил грамматики. Чтобы показать, каким образом структура цепочек отображается в правила грамматики, рассмотрим следующие примеры. 1. Цепочке, состоящей из заданных символов abc, соответствует правило

<I>abc.

2. Цепочке, начинающейся с заданного символа a, соответствует правило

<I>a<A>.

 3. Цепочке, заканчивающейся заданным символом a, соответствует правило

<I><A>a.

4. Цепочке, начинающейся и заканчивающейся заданными символами a, b, соответствует правило

<I> a<A>b.

5. Цепочке, содержащей в середине символ a, соответствует правило

<I><A>a<B>.

6. Цепочке заданной длины l =2 соответствуют правила:

<A>a<B> и <B>a.

7. Цепочке, состоящей из повторяющихся символов a, соответствуют правила

<A>a<A> и <A>a.

 8. Цепочке, состоящей из чередующихся символов a и b, соответствуют правила:

<A>a<B> и <B>b<A>.

В общем случае, если описано множество цепочек, представляющих собой некоторый язык, и требуется построить грамматику, порождающую это множество цепочек, то следует поступать так:

1) Выписать несколько примеров из заданного множества цепочек. 2) Проанализировать структуру цепочек, выделяя начало, конец, повторяющиеся символы или группы символов. 3) Ввести обозначения для сложных структур, состоящих из групп символов. Такие обозначения являются нетерминальными символами искомой грамматики. 4) Построить правила для каждой из выделенных структур, используя для задания повторяющихся структур рекурсивные правила. 5) Объединить все правила. 6) Проверить с помощью выводов возможность получения цепочек с разной структурой.

7. КС-грамматики. Приведеные грамматики.

2.1 Приведенные грамматики. Из четырех типов грамматик контекстно-свободные грамматики являются наиболее важными с точки зрения приложений к языкам программирования и компиляции. С помощью КС-грамматики можно определить большую часть структуры языка программирования. При построении грамматик, задающих конструкции языков программирования, часто приходится прибегать к их преобразованию, чтобы порождаемый язык приобрел нужную структуру, поэтому вначале рассмотрим несколько достаточно простых, но важных преобразований КС-грамматик. Первый вид преобразования связан с удалением из грамматики бесполезных символов. Бесполезные символы в грамматике могут оказаться в следующих случаях: а) если символ не может быть получен при выводе, б) если из символа не может быть получена конечная терминальная цепочка (получается бесконечная цепочка или нет правил, приводящих к терминальной цепочке).

Вначале рассмотрим алгоритм выявления символов, из которых нельзя вывести конечные цепочки.

Определение. КС-грамматика называется приведенной, если она  не содержит бесполезных символов.

8. Бесполезные символы. Удаление бесполезных символов.

Определение непроизводящих символов. Определение. Символ <X> VA называется непроизводящим, если из него не может быть выведена конечная терминальная цепочка.

Рассматривая правила грамматики,  можно сделать  вывод,  что если все символы правой части являются производящими, то производящим является и символ, стоящий в левой части. Последнее утверждение позволяет написать процедуру обнаружения непроизводящих символов в следующем виде:     1. Составить список нетерминалов,  для которых найдется хотя  бы одно правило, правая часть которого не содержит нетерминалов.     2. Если найдено такое правило,  что все нетерминалы, стоящие  в его правой части уже занесены в список,  то добавить  в  список  нетерминал, стоящий в его левой части.     3. Если на шаге 2 список больше не пополняется,  то  получен  список всех производящих нетерминалов грамматики,  а все нетерминалы не попавшие в него являются непроизводящими. Анализируя в соответствии с приведенными правилами следующую грамматику : Г3. 0: R = {<I>a<I>a, <I>b<A>d, <I>c, <A>c<B>d, <A>a<A>d, <B>d<A>f  }, находим, что здесь непроизводящими являются символы <А> и <В>. После удаления правил, содержащих непроизводящии символы, получаем:   R' = {<I> a<I>a, <I> c}. Определения недостижимых символов. Определение.  Символ X Vт VA  называется недостижимым в КС-грамматике Г, если X не появляется ни в одной выводимой цепочке.

• Рассматривая правила грамматики, можно заметить , что если нетерминал в левой части правила является достижимым , то и все символы правой части являются достижимыми. Это свойство правил является основой процедуры выявления недостижимых символов, которую можно записать так:

  1. Образовать одноэлементный список, состоящий из начального символа

  2. Если найдено правило, левая часть которого уже имеется в списке, то включить в  список все символы, содержащиеся в его правой части.

  3.  Если на шаге 2 новые нетерминалы в список больше  не  добавляются,  то получен список всех достижимых нетерминалов, а нетерминалы, не попавшие в список, являются недостижимыми.

Например, применяя приведенные правила к следующей грамматике: Г_{3. 1} :      R = { <I> a<I>b, <I> c, <A> b<I>, <A> a   },

находим, что A является недостижимым символом.

  Определения бесполезных символов.

Бесполезный символ грамматики можно определить следующим образом:

Определение. Символ X, который принадлежит VтU Va называется бесполезным в  КС-грамматике Г, если он является недостижимым или непроизводящим.

Исключить бесполезные символы из грамматики можно удаляя правила, содержащие вначале непроизводящие, а затем недостижимые символы. В качестве иллюстрации применения приведенных правил выполним преобразование следующей грамматики:

 Г_{3. 2} : R = {<I>ac

<I> b<A>, <A> c<B><C>, <B> a<I><A>, <C> bc, <C> d  }.

Вначале находим, что <А> и <В> являются непроизводящими символами и, исключая правила с непроизводящими символами , получаем: R' = {<I>ac          <C> bc,          <C> d  }.

В полученной схеме символ <C>  является недостижимым символом. Исключая правила, содержащие этот символ, получаем: R" = {<I>ac  }.

9. Цепные правила. Исключение цепных правил.

Определение. Правило грамматики вида <A>  <B>,  где <A>,<B> VA,                           называется цепным.

Утверждение. Для КС-грамматики Г, содержащей цепные правила , можно                   построить эквивалентную ей грамматику Г', не содержащую цепных правил.

Идея доказательства заключается в следующем. Если схема грамматики имеет вид   R = {...,<A>  <B>,...,<B>  <C>, ... , <C> a<X> },

то такая грамматика  эквивалентна грамматике со схемой   R' = {...,<A>  a<X>,...},

поскольку вывод в грамматике со схемой R цепочки a<X> :

<A>  B>  <C> a<X>

может быть получен  в грамматике со схемой R' с помощью правила <A>  a<X>. В общем случае доказательство последнего утверждения можно выполнить так. Разобьем R на два подмножества R₁ и R₂, включая в R₁ все правила вида <A>  B>. Для каждого правила из R₁ найдем множество правил S(<A_i>), которые строятся так: если <A_i>  * <A_j> и в R₂ есть правило <A_j>   , где  - цепочка словаря (V_т V_A)^* , то в S(<A_i>) включим правило <A_i>      . Построим новую схему R' путем объединения правил R₂ и всех построенных множеств S(<A_i>). Получим грамматику Г' = {V_т ,V_a , I , R'}, которая эквивалентна заданной и не содержит правил вида <A>  <B>. В качестве примера выполним исключение цепных правил из грамматики Г_{1. 9} со схемой :

Г_{1. 9}:      R={<E>    <E> + <T> | <T>,                   < T>  T> * <F> | <F>,                    <F>  ( <E> ) | a}.

Вначале разобьем правила грамматики на два подмножества:   R₁ = { <E>  <T>,<T>    <F> } , R₂ = { <E>  <E>+<T>, <T>  <T>*<F>, <F>(<E>) | a }

Для каждого правила из R1 построим соответствующее подмножество.  

S(<E>) = { <E>  T>*<F>, <E> (<E>) | a }, S(<T>) = { <T>  (<E>) | a}

В результате получаем искомую схему грамматики без цепных правил в виде:

R2 U S(<E>) U S(<T>) = { <E>  --> <T>+<T> | <T>*<F> | (<E>) | a,

<T>  <T>*<F> | (<E>) | a, <F>  (<E>) | a }

Последний вид рассматриваемых преобразований связан с удалением из грамматики правил с пустой правой частью.

Определение. Правило вида <A>  $ называется аннулирующим правилом.

10. Не укорачивающие грамматики. Построение не укорачивающих грамматик.

Определение. Грамматика называется неукорачивающей или грамматикой без аннулирующих правил, если либо  1)схема грамматики не содержит аннулирующих правил,  2)либо схема грамматики содержит только одно правило вида <I>  $, где <I> - начальный символ грамматики, и символ I не встречается в правых частях остальных правил грамматики.

Для грамматик, содержащих аннулирующие правила, справедливо следующее утверждение.

Утверждение. Для каждой КС-грамматики Г', содержащей аннулирующие правила, можно  построить эквивалентную ей неукорачивающую грамматику Г, такую что L(Г')=L(Г).

Построение неукорачивающей грамматики предполагает увеличение числа правил заданной грамматики путем построения дополнительных правил, получаемых в результате исключения нетерминалов аннулирующих правил. Чтобы построить дополнительные правила необходимо выполнить все возможные подстановки пустой цепочки вместо аннулирующего нетерминала во все правила грамматики. Если же в грамматике есть правило вида <I>  $ и символ <I> входит в правые части других правил грамматики, то следует ввести новый начальный символ <I'> и заменить правило <I>  $ двумя новыми правилами: <I'>  $ и <I'> <I> . В качестве иллюстрации способа построения неукорачивающих грамматик, исключим аннулирующие  правила из следующей грамматики:

                                                       Г_{3. 3} :       R = { <I>  a<I>b<I>,                                                                                 <I>  b<I>a<I>,                                                                                 <I>    $ } Выполняя все возможные замены символа I в первом правиле грамматики, получаем четыре правила вида:  

<I>  a<I>b<I>,   <I>  ab<I>,    <I> a<I>b,    <I> ab .

Поступая аналогично со вторым правилом, имеем:  

<I> b<I>a<I>,    <I> ba<I>,    <I>  b<I>a,    <I>  ba.

Учитывая, что начальный символ, образующий аннулирующее правило, входит в правые части других правил грамматики, заменим правило <I>  $ правилами вида <I'> $  и  <I'> <I> . Построенная совокупность правил образует схему искомой неукорачивающей грамматики. Все приведенные выше преобразования грамматик могут быть использованы и оказаться полезными при построении как конечных, так и магазинных автоматов.

11. Конечный автомат. Определение. Структура.

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Грамматики типа три называются автоматными, потому что существует связь между этими грамматиками и конечными автоматами без выходов или распознавателями. Модель такогораспознавателя состоит из входной ленты, читающей головки и устройства управления, как это показано на рис. 2.1.

При изучении формальных языков обычно предполагают, что слово, подаваемое на вход распознавателя, предварительно записывается на бесконечную входную ленту, ограниченную с одной стороны. Лента разделена на части, в каждой из которых может быть расположен один символ входного алфавита. Входное слово распола­гается всегда , начиная от левого края ленты. Предполагается также, что незаполненные ячейки, расположенные правее входного слова, содержат пустые символы, которые обозначаются греческой буквой ε

 

 

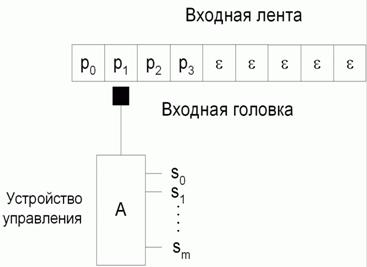
Рис. 2.1.  Модель распознавателя

Чтение символов входного алфавита производится читающей головкой, которая после считывания символа сдвигается на одну позицию вправо. Прочитанный таким образом символ подаётся на вход устройства управления, которое может изменять свое состояние. Такой распознаватель (A)может быть определен совокупностью пяти компонентов:

А = { P, S, s₀, φ, F},

где P - входной алфавит распознавателя, содержащий символы, записываемые на входную ленту,

S - множество состояний распознавателя,

s₀ - начальное состояние, которым является одно из состояний множества S,

φ - функция переходов, задающая отображение

φ : P×S → S

F - множество конечных состояний, которое должно быть подмножеством S,

Эта функция каждой паре: состояние и входной символ ставит в соответствие состояние распознавателя. В функциональной форме она записывается так:

φ (s_i, p_k) = s_m.

На практике функцию переходов задают в виде двумерной таблицы, которую называют таблицей переходов распознавателя, или в виде ориентированного графа, называемого диаграммой переходов распознавателя. При построении таблицы переходов ее строки отмечаются состояниями распознавателя, а столбцы обозначаются входными символами. В каждой клетке таблицы, которая соответствует строке, отмеченной состоянием s_i, и столбцу, отмеченному входным символом p_k, записывается состояние s_m, определяемое функцией переходов φ(s_i, p_k) = s_m. Примером таблицы переходов распознавателя является таблица 2.1. Состояния распознавателя в этой таблице обозначены буквами латинского алфавита, а входной алфавит состоит из цифр 0 и 1.

Чтобы построить диаграмму переходов распознавателя, нужно каждому состоянию сопоставить вершину графа и пометить эту вершину символом состояния, а каждому переходу, определяемому функцией φ (s_i, p_k) = s_m, дугу графа s_m, отмеченную входным символом p_k и соединяющую вершины s_i, и s_m . Диаграмма переходов распознавателя, заданного табл. 2.1, изображена на рис. 2.1

Работа распознавателя может быть представлена в виде последовательности тактов. Чтобы описать работу распознавателя, введём понятие конфигурации. Конфигурация распознавателя определяется состоянием s_i и ещё не прочитанной частью входной цепочки α’ на ленте:

(s_i, α’).

В каждом такте происходит смена конфигурации распознавателя. Если такту работы соответствует конфигурация (s_k,pα'), где p- символ, расположенный под читающей головкой, и, если определена функция переходов j(s_k,p)=s_i, то формируется новая конфигурация (s_i, α'), соответствующая следующему такту работы.

Смену конфигураций обозначают специальным символом и записывают так:

(s_k,α) |-- (s_i, α').

Если существует последовательность конфигураций, соответствующая  последовательности тактов работы распознавателя А

(s_i, α₁) |-- (s_i2, α₂) |-- ... |-- (s_ik, α_k),

то её обозначают следующим образом:

(s_i1, α₁) |-- ^* (s_ik, α_k)

Конфигурация, образованная начальным состоянием s₀ и ещё не прочитанной входной цепочкой α называется начальной конфигурацией и обозначается (s₀, α).

Конфигурация, образованная конечным состоянием из множества F и пустой цепочкой, называется конечной или заключительной конфигурацией.

Используя введённые термины, можно определить два новых понятия.

Определение. Входное слово (цепочка) α называется допустимым для распознавателя А, если при последовательном чтении символов α с входной ленты распознаватель переходит из начальной конфигурации в одну из конечных конфигураций.

(s₀, α) |-- ^* (s_k,$) и s_k Î F

Определение. Множество цепочек L, допускаемых распознавателем А, назовём языком, допускаемым этим распознавателем L(А).

L(А) = { α | α Î P* и (s₀, α) |-- ^* (s_k,$) и s_k Î F}

В качестве иллюстрации рассмотрим работу распознавателя А_1,  который определятся множествами: P = {0, 1}, S = {A, B, C, D}, F = {D}. Функция переходов этого распознавателя задаётся таблицей 2.1.

 

Таблица 2.1. Таблица переходов  распознавателя А₁

pk si	0	1
A	B	A
D	C	A
C	D	C
D	-	-

 

Этой таблице соответствует диаграмма переходов, изображенная на рис. 2.2

 

Рис. 2.2. Диаграмма переходов распознавателя А₁.

Работа распознавателя для  входной цепочки 01001 может быть представлена в виде последовательности конфигураций

(A,01001) |-- (B,1001) |-- (A,001) |-- (B,01) |-- (C,1) |-- (C,$),

которая показывает, что цепочка не допускается распознавателем А₁, поскольку он не достигает конечного состояния после прочтения всех входных символов.

Введенные понятия позволяют определить связь между формальными грамматиками и распознавателями путем установления соответствия языков, порождаемых грамматиками, и языков, допускаемых распознавателями.

12. Построение конечного автомата по автоматной грамматике.

Утверждение. Если заданный конечный язык не содержит слов, являющихся начальными отрезками другого слова этого языка, то для него можно построить детерминированный конечный распознаватель.

В качестве примера построим распознаватель, определяющий принадлежность слов к заданному языку, который состоит из трехбуквенных слов двоичного алфавита V_т = {0,1}, содержащих две единицы:

L₁= { 011, 101, 110 }

Построим А-грамматику, порождающую этот язык. В качестве нетерминальных символов будем использовать прописные буквы латинского алфавита. Начальный символ грамматики обозначим <I>. Все слова начинаются либо с 0, либо с 1, поэтому построим правила <I>  0 <A>, <I>  1 <B>. Слова, начинающиеся с 0, в качестве второго символа имеют 1 , следовательно, построим  правило <A>  1 <C>. Слова, начинающиеся с 1, имеют второй буквой 0 или 1, поэтому построим правило <B>  0<D> и <B>  1<E> . Конечные правила должны иметь вид, определяемый последней буквой каждого слова, следовательно получаем правила <C>  1, <D>  1, <E>  0.

В результате получаем схему искомой грамматики в виде:

R = {<I>  0 <A>, <I>  1 <B>, <A>  1 <C>, <B>  0<D>, <B>  1 <E>, <C>  1, <D>  1, <E>  0}.

Обозначим состояния искомого распознавателя нетерминальными символами грамматики и добавим два символа Z и U для обозначения заключительных состояний. Дополним заключительные правила построенной грамматики символом Z. Затем для всех состояний, из которых не определены переходы для какого-либо входного символа, добавим переход из этих состояний в заключительное состояние U. В результате получаем диаграмму переходов распознавателя, изображенную на рис. 2.12.

Рис. 2.12. Диаграмма переходов распознавателя, определяющего принадлежность цепочки к языку L₁

Для того чтобы построить распознаватель, определяющий, какое из слов входного языка подано на вход, заключительные правила построенной грамматики нужно дополнить не одним символом Z , а тремя различными символами: Z1, Z2, Z3. В результате получаем диаграмму переходов распознавателя, изображенную на рис. 2.13.

Рис. 2.13. Диаграмма переходов распознавателя входных цепочек языка L₁

Распознаватели, построенные описанным способом, как правило, обладают избыточными состояниями. Такие состояния можно объединить с другими состояниями, не нарушая заданных функций распознавателя. Правила выявления и объединения состояний строятся  на основе отношения эквивалентности, которое рассматривается в следующем параграфе.

13. Лексический анализатор.