Компиляторы. Этапы компиляции программ.
Транслятор может быть интерпретирующего или компилирующего типа. В первом случае его называют интерпретатором входного языка, а во втором - компилятором.
Интерпретатор последовательно читает предложения входного языка, анализирует их и сразу же выполняет, а компилятор не выполняет предложения языка, а строит программу, которая может в дальнейшем быть запущена для получения результата.
На вход компилятора подается текст, написанный на входном языке - языке, понятном человеку, а результатом работы компилятора является текст на языке, понятном устройству.
1.1.2. Стадии работы компилятора
Работа компилятора состоит из нескольких стадий, которые могут выполняться последовательно, либо совмещаться по времени. Эти стадии могут быть представлены в виде схемы.
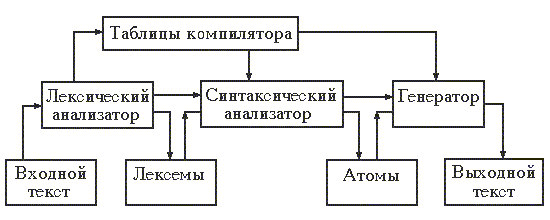
Первая стадия работы компилятора называется лексическим анализом, а программа, её реализующая, - лексическим анализатором (ЛА). На вход лексического анализатора подаётся последовательность символов входного языка. ЛА выделяет в этой последовательности простейшие конструкции языка, которые называют лексическими единицами. Примерами лексических единиц являются идентификаторы, числа, символы операций, служебные слова и т.д. ЛА преобразует исходный текст, заменяя лексические единицы их внутренним представлением - лексемами. Лексема может включать информацию о классе лексической единицы и её значении. Кроме того, для некоторых классов лексических единиц ЛА строит таблицы, например, таблицу идентификаторов, констант, которые используются на последующих стадиях компиляции.
Вторую стадию работы компилятора называют синтаксическим анализом, а соответствующую программу - синтаксическим анализатором (СА). На вход СА подается последовательность лексем, которая преобразуется в промежуточный код, представляющий собой последовательность символов действия или атомов. Каждый атом включает описание операции, которую нужно выполнить, с указанием используемых операндов. При этом последовательность расположения атомов, в отличие от лексем, соответствует порядку выполнения операций, необходимому для получения результата.
На третьей стадии работы компилятора осуществляется построение выходного текста. Программа, реализующая эту стадию, называется генератором выходного текста (Г). Генератор каждому символу действия, поступающему на его вход, ставит в соответствие одну или несколько команд выходного языка. В качестве выходного языка могут быть использованы команды устройства, команды ассемблера, либо операторы какого-либо другого языка.
Рассмотренная схема компилятора является упрощенной, поскольку реальные компиляторы, как правило, включают стадии оптимизации.
Основные определения формальной грамматики.
1.2.1. Первичные понятия
Определение. Конечное множество символов, неделимых в данном рассмотрении, называется словарем или алфавитом, а символы, входящие в множество, - буквами алфавита.
Например, алфавит A = {a, b, c, +, !} содержит 5 букв, а алфавит B = {00, 01, 10, 11} содержит 4 буквы, каждая из которых состоит из двух символов.
Определение. Последовательность букв алфавита называется словом или цепочкой в этом алфавите. Число букв, входящих в слово, называется его длиной.
Например, слово в алфавите A a=ab++c имеет длину l(a) = 5, а слово в алфавите B b=00110010 имеет длину l (b) = 4.
Если задан алфавит A, то обозначим A* множество всевозможных цепочек, которые могут быть построены из букв алфавита A. При этом предполагается, что пустая цепочка, которую обозначим знаком $, также входит в множество A*.
Определение. Формальной порождающей грамматикой Г называется следующая совокупность четырех объектов: Г = { Vт, VA, <I> VA, R },
где Vт - терминальный алфавит (словарь); буквы этого алфавита называются терминальными символами; из них строятся цепочки порождаемые грамматикой;
VA - нетерминальный, вспомогательный алфавит (словарь); буквы этого алфавита используются при построении цепочек; они могут входить в промежуточные цепочки, но не должны входить в результат порождения;
<I> - начальный символ грамматики <I> VA.
R - множество правил вывода или порождающих правил вида , где и - цепочки , построенные из букв алфавита Vт VA, который называют полным алфавитом (словарем) грамматики Г.
В множество правил грамматики могут также входить правила с пустой правой частью вида <Е> . Чтобы избежать неопределенности из-за отсутствия символа в правой части правила, условимся использовать символ пустой цепочки, записывая такое правило в виде <Е> $.
Чтобы установить правила построения цепочек, порождаемых грамматикой , введем следующие понятия.
Определение. Пусть r = - правило грамматики Г и = ' " - цепочка символов, причем', " (Vт VA) *. Тогда цепочка = ' " может быть получена из цепочки путем применения правила r (т.е. заменой в m цепочки на ). В этом случае говорят, что цепочка непосредственно выведена из цепочки и обозначают . Определение. Если задана совокупность цепочек = ( 0, 1,...,n), таких что существует последовательность непосредственных выводов: 0 1, 1 2, ... , n-1 n, то такую последовательность называют выводом n из 0 в грамматике Г и обозначают 0 * n. Определение. Множество конечных цепочек терминального алфавита Vт грамматики Г, выводимых из начального символа <I>, называется языком, порождаемым грамматикой Г и обозначается L( Г). L( Г ) = {Vт* | <I> * }. |