Глава 3. Обработка экспериментальных данных методом опорных векторов с составным шагом.

При обработке экспериментальных данных часто приходится решать так называемые "обратные задачи". Смысл этих задач состоит в обращении причинно-следственной связи – по данным наблюдений (следствиям) определяются характеристики объекта (причины).

Во многих случаях задача обработки экспериментальных данных может быть представлена в виде системы m уравнений в n-мерном пространстве [3, c.361]:

K    f,

(3.1)

где  – искомый вектор размерности n , f – вектор измерительных данных размерности m ,  – вектор ошибок измерений размерности m, K – преобразующая матрица. K может быть единичной матрицей (в задачах сглаживания изображений), оператором, описывающим аппаратные искажения, матрицей, при помощи которой производится интерполяция измеренных данных и т.п. Такого рода задачи относятся к разряду некорректных [4], и для получения удовлетворительного результата требуется использовать априорную информацию о моделируемом процессе, причем качество решения существенно зависит от полноты используемой информации.

Пусть далее V – ковариационная матрица ошибок, W=V^-1 , D ^p – матрица численного дифференцирования, - p-ая степень матрицы D. = ( )^T – стабилизатор p-го порядка, с его помощью в решение вводится априорная информация о гладкости модельной функции.

Общая регуляризованная оценка вектора  может быть получена в виде [5 ],[7].

 = ( KTWK +  ) -1KT Wf,

(3.2)

или

 =  2p-1KT (  2K KT + V )-1 f,

(3.3)

где = ^-1/2,  - параметр регуляризации, который можно вычислить по формуле[7]:

 =

(3.4)

Алгоритм 1.

Решение обратной задачи обработки экспериментальных данных нахождением классической оценки.

Шаг 1. Формируются матрицы ,D ^p, W.

Шаг 2. Ищется параметр регуляризации .

Шаг 3. Ищется регуляризованная оценка.

Для анализа работы алгоритма и программы можно провести численный эксперимент. Основой модельного сигнала может быть выбран так называемый лоренцевский контур, имитирующий сигнал, характерный для прикладной спектроскопии

f(x) =

(3.5)

где параметр a – амплитуда модельной функции, b - положение центра, с - полуширина. С помощью генератора псевдослучайных чисел к модельному сигналу добавлялись “ошибки измерений” заданного уровня. Полученный “экспериментальный сигнал” подвергался дальнейшей обработке.

Файл-сценарий для получения классической статистической регуляризованной оценки:

% Метод статистической регуляризации (классическая оценка)

% a, b, c - параметры лоренциана: a - амплитуда, b - положение центра, c – полуширина

% x1, x2 - границы интервала измерений, n - число измерений, err - уровень ошибок

clear

a=1;b=0.5;c=0.03;x1=0;x2=1;n=300;err=0.1;

k=eye(n); %преобразующая матрица

%(единичная для сглаживания)

[f,f1,x,dx]=test(a,b,c,n,x1,x2,err); %формирование тестовой функции,

%f-точная функция,

%f1-экспериментальная,dx- шаг,

%x-ось абсцисс(для графика)

[dif,omega,w,v]=matrixs(n,err,dx); %матрицы: dif-дифференцирования(2 порядка)

%omega-стабилизатор,

%w-информационная матрица, %v-ковариационная матрица ошибок,

alf=alfa(f1,v,k,omega);

%параметр регуляризации (одношаговая оценка)

ff=inv(k'*w*k+alf*omega)*(k'*w*f1');

plot(x,f,x,f1,x,ff)

Файл-функция для расчета матриц дифференцирования, стабилизатора, ковариационной матрицы ошибок:

function[dif,omega,w,v]=matrixs(n,err,dx)

% вспомогательные матрицы для МСР

% dif1-матрица дифференцирования первого порядка

% dif-матрица дифференцирования второго порядка

% omega-матрица гладкости

% v-ковариационная матрица ошибок

% w-обратная к ней

g=-ones(1,n-1);

b=eye(n);

c=diag(g,-1);

dif1=(b+c)*(1/dx);

dif=dif1*dif1;

omega=dif'*dif;

s=err^2;

s=1/s;

w=s*eye(n);

v=inv(w);

Файл-функция для расчета параметра регуляризации:

function alf=alfa(f1,v,k,omega)

% одношаговая оценка параметра регуляризации

% k-преобразующая матрица, f - вектор ошибок измерений

% omega - стабилизатор, v - ковариационная матрица ошибок

alf=(trace(k*pinv(omega)*k'))/((f1*f1')-trace(v));

Файл-функция для формирования модельной функции и «экспериментальных данных»:

function [f,f1,x,dx]=test(a,b,c,n,x1,x2,err)

dx=(x2-x1)/n;

for i=1:n

x(i)=x1+dx*i;

f(i)=a/((x(i)-b)^2+c);

end

f=f/max(f);

f1=f+(randn(n,1)*err)';

Полученные результаты можно представить графически при помощи функции plot (plot(x,f,x,f1,x,ff)).

Рис.1. Результаты обработки экспериментальных данных (сглаживание). Уровень шума-20% от максимального значения модельной функции. Сплошная кривая – модельная функция, + – “экспериментальные” данные, уровень шума – 10% от максимального значения модельной функции. * – сглаженные данные.

Качество обработки можно также оценить при помощи погрешностей восстановления (мер различия) [8].

,

.

Здесь – вектор восстановленных значений экспериментальной функции; – вектор значений модельной функции:

,

.

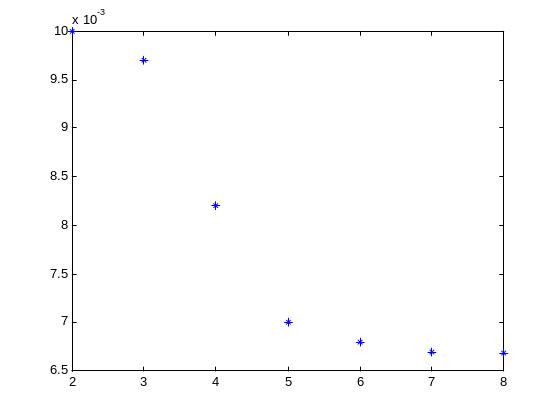
Рис.2. Среднеквадратичная мера отличия () восстановленного сигнала от модельного в зависимости от уровня шума.

Файл-функция для определения мер различия:

function[sqo,h]=mera(f1,f2)

% f1 - восстановленная функция, f2 - модельная

n=length(f1);

sqo=0;h=0;h1=0;

for i=1:n

sqo=sqo+(f1(i)-f2(i))^2;

h=h+abs(f1(i)-f2(i));

h1=h1+abs(f1(i));

end

sqo=sqrt(sqo)/n;

h=h/h1;

При построении классической статистической регуляризованной оценки учитывается априорная информация первого рода о гладкости модельной искомой функции, описывающей восстанавливаемое изображение и аппроксимируемой вектором  и о предполагаемом уровне ошибок эксперимента, но в них не может быть отражена априорная информация второго рода, представимая в виде неравенств.

В [5] указано, что одним из статистически эквивалентных способов учета гладкости является дополнение уравнения (3.1), умноженного на невырожденную матрицу H, уравнением, учитывающим желаемую гладкость p-го порядка модельной функции, аппроксимируемой вектором :

HK +  = Hf	(3.6)
D p +  = 0	(3.7)

где =H.

Если матрица H такова, что H^TH=W, то решение системы (3.6), (3.7) с минимальной суммой + , совпадает со статистической регуляризованной оценкой. Для того, чтобы учесть при решении априорную информацию, представимую в виде неравенств, целесообразно построить некую итерационную процедуру, позволяющую по ходу итераций учесть ограничения на модельную функцию.

Исключим  из (3.6) с помощью уравнения (3.7)

(3.8)

Система уравнений (8) совместна, так как нетрудно убедиться, что, в частности, является ее решением. Так матрица H – невырожденная матрица порядка n, то матрица А (порядка ) будет невырожденной, а система (3.8) будет совместной неопределенной системой линейных уравнений. В [5] установлена связь решения минимальной норма системы (3.8):

(3.9)

с регуляризованной оценкой (3.4). Искомую статистическую регуляризованную оценку получим из (3.7):

(3.10)

Одним из широко применяемых итерационных методов решения систем линейных уравнений является метод последовательного проектирования, который для системы линейных уравнений в пространстве R^N

(3.11)

в варианте с циклическим перебором уравнений выглядит так:

(3.12)

где x⁽⁰⁾ –произвольная точка из R^N, i_k = mod_M(k)+1.

Метод (3.12) генерирует последовательность точек, сходящуюся к решению системы (3.8), наиболее близкое к x⁽⁰⁾. Естественным критерием остановки метода (3.12) является достижение достаточно малого максимального модуля невязки.

Далее -приближенным решением системы уравнений 3.8) будем считать любое решение системы линейных неравенств:

,

(3.13)

где  – достаточно малое положительное число. В [10], [11] для отыскания -приближенного решения системы (3.8) построен метод опорных векторов с составным шагом, который является реализацией метода последовательного проектирования с циклическим перебором уравнений и пропуском малонарушенных уравнений. Если система уравнений (3.8) совместна, то алгоритм, основанный на методе опорных векторов остановится за конечное число шагов, при этом последняя точка x^(k) ,будет -приближенным решением системы уравнений (3.8).

Агоритм 2.

Решение систем линейных уравнений методом опорных векторов с составным шагом.

0. Пусть x⁽⁰⁾ – произвольная точка из R^N. Положим k=0, i=1, l=0. Выберем достаточно малое положительное число .

1. Если , то положим l=l+1 и перейдем к п.3.

2. Вычислим , положим k=k+1, l=1.

3. Если i<M, то положим i = i + 1, иначе положим i = 1.

4. Если l < M, то перейдем к п. 1, иначе останов; x^(k) – -приближенное решение системы уравнений (6).

Файл-сценарий, тестирующий работу алгоритма 2:

% тест для решения системы линейных алгебраических уравнений

% решение х=[5 -4.4 -2.2]

eps=0.000001; %точность итераций

a=[3 2 1;5 4 2]; %матрица системы

b=[4 3]; %вектор правой части

b=b';

x0=[0 0 0];

x=algorithm2(a,b,x0,eps)

Файл-функция для решения систем линейных уравнений:

function[x]=algorithm2(a,b,x0,eps)

% a - матрица системы, b - вектор правой части

% x0 - начальное приближение, eps - заданная точность итераций

[m,n]=size(a);

x=x0;

l=0;k=0;

while l<m

for i=1:m

if abs(a(i,:)*x'-b(i))<=eps*evcnorm(a(i,:))

l=l+1;

else

x=x-((a(i,:)*x'-b(i))/((evcnorm(a(i,:))^2)))*a(i,:);

k=k+1;

l=1;

end

end

end

Файл-функция для нахождения евклидовой нормы вектора:

function [s]=evcnorm(a)

% евклидова норма вектора

n=length(a);

s=0;

for i=1:n

s=s+a(i)^2;

end

s=sqrt(s);

Предположим теперь, что  не может быть, например, отрицательным. Тогда следует дополнить систему уравнений (3.8) системой линейных неравенств:

.

(3.14)

Опишем простой алгоритм метода опорных векторов с составным шагом для решения систем неравенств, заданных в пространстве R^N.

, .

Алгоритм 3.

Решение систем линейных алгебраических уравнений методом опорных векторов с составным шагом.

0. Пусть x⁽⁰⁾ - произвольная точка из R^N. Положим k = 0, i = 1, l = 0. Выберем достаточно малое положительное число .

1. Если , то положим l=l+1 и перейдем к п.3.

2. Вычислим , положим k=k+1, l=1.

3. Если i < L, то положим i = i + 1, иначе положим i = 1.

4. Если l < L, то перейдем к п. 1, иначе останов; x^(k) – -приближенное решение системы (9).

Файл-сценарий, тестирующий работу алгоритма 3:

%тест для решения системы линейных алгебраических неравенств

eps=0.000001; %точность итераций

a=[9 1;9 -1]; %матрица системы

b=[0 0]; %вектор правой части

b=b';

x0=[-1 1];

x=algorithm3(a,b,x0,eps)

Файл-функция для решения систем неравенств:

function[x]=algorithm3(a,b,x0,eps)

% a - матрица системы, b - вектор правой части

% x0 - начальное приближение, eps - заданная точность итераций

[m,n]=size(a);

x=x0;

l=0;k=0;

while l<m

for i=1:m

if (a(i,:)*x')>=b(i)

l=l+1;

else

x=x-((a(i,:)*x'-b(i)-eps)/((evcnorm(a(i,:))^2)))*a(i,:);

k=k+1;

l=1;

end

end

end

Для отыскания - решения системы уравнений (3.8), удовлетворяющего неравенствам (3.14) предлагается использовать комбинацию алгоритмов 2,3.

Алгоритм 4.

Решение систем линейных уравнений с ограничениями методом опорных векторов с составным шагом

0. Пусть x⁰- произвольная точка из R^N. Положим k = 0, p₂ = 1. Выберем достаточно малое положительное число .

1. Положим i = 1, l = 0, p₁ = 0.

2. Если , то положим l=l+1 и перейдем к п.4.

3. Вычислим , положим k = k + 1, l = 1, p₁ = 1.

4. Если i < M, то положим i = i + 1, иначе положим i = 1.

5. Если l < M, то перейдем к п. 1.

6. Если p₁+ p₂ = 0, то останов, x^(k) – решение системы (6), (9).

7. Положим i = 1, l = 0, p₁ = 0, p₂ = 0.

8. Если , то положим l=l+1 и перейдем к п. 10.

9. Вычислим , положим k=k+1, l=1, p₂ = 1.

10. Если i < L, то положим i = i + 1, иначе положим i = 1.

11. Если l < L, то перейдем к п.8.

12. Если p₁+ p₂ > 0, то положим p₂ = 0 и перейдем к п. 1, иначе останов: x^(k) – -приближенное решение системы (3.8), (3.14).

Файл-сценарий для решения систем линейных уравнений с ограничениями:

% тест для решения системы линейных алгебраических уравнений с ограничениями

epse=0.000001; %точность итераций

epsne=0.000001;

a=[3 2 1;5 4 2]; %матрица системы

b=[4 3]; %вектор правой части

b=b';

x0=[0 0 0];

c=eye(3);

d=[0 0 0];

d=d';

x=algorithm4(a,b,c,d,x0,epse,epsne)

Файлы-функции для решения систем линейных уравнений с ограничениями:

function[x]=algorithm4(a,b,c,d,x0,epse,epsne)

% a - матрица системы, b - вектор правой части

% x0 - начальное приближение; epse, epsne - заданные точности итераций

k=0;p2=1;p1=1;x=x0;

while((p1+p2)~=0)

[x,p1,k]=equation(a,b,x,epse,k);

[x,p2,k]=nonequation(c,d,x,epsne,k);

end

function [x,p1,k]=equation(a,b,x,eps,k);

[m,n]=size(a);p1=0;

l=0;

while l<m

for i=1:m

if abs(a(i,:)*x'-b(i))<=eps*evcnorm(a(i,:))

l=l+1;

else

x=x-((a(i,:)*x'-b(i))/((evcnorm(a(i,:))^2)))*a(i,:)

k=k+1;

p1=1;

l=1;

end

end

end

function[x,p2,k]=nonequation(a,b,x,eps,k);

[m,n]=size(a);

l=0;p2=0;

while l<m

for i=1:m

if (a(i,:)*x')>=b(i)

l=l+1;

else

x=x-((a(i,:)*x'-b(i)-eps)/((evcnorm(a(i,:))^2)))*a(i,:);

k=k+1;p2=1;

l=1;

end

end

end

Если множество решений системы неравенств с_i, x  d_i (i=1,….,L) содержит шар радиуса 2 , то, как показано в [11], метод опорных векторов с составным шагом для решения систем неравенств позволит получить решение за конечное число итераций. Учитывая специфику системы (3.8), можно утверждать, что алгоритм, реализующий метод опорных векторов с составным шагом даст, решение системы (3.8) за один цикл просмотра неравенств системы.

Для отыскания -решения системы (3.8), удовлетворяющего неравенствам вида (3.14) построен алгоритм, представляющий комбинацию методов опорных векторов с составным шагом для решения систем линейных уравнений и систем неравенств.

Для учета матрицы , необходимой для решения системы (3.8), изменим немного функцию matrixs ,таким образом она будет выглядеть так:

function[dif,omega,w,v,u]=matrixs(n,err,dx)

%вспомогательные матрицы для МСР

%dif1-матрица дифференцирования первого порядка

%dif-матрица дифференцирования второго порядка

%omega-матрица гладкости

%v-ковариационная матрица ошибок

%w-обратная к ней

%u-матрица, необходимая при учете неравенств

g=-ones(1,n-1);

b=eye(n);

c=diag(g,-1);

dif1=(b+c)*(1/dx);

dif=dif1*dif1;

omega=dif'*dif;

s=err^2;

s=1/s;

w=s*eye(n);

v=inv(w);

a=ones(1,n)*(err^2);

u=diag(a);

u=inv(u);

% Метод статистической регуляризации + метод опорных векторов

% с составным шагом

% a ,b, c - параметры лоренциана: a - амплитуда, b - положение центра,

% c - полуширина

% x1, x2 - границы интервала измерений, n-число измерений, err-уровень ошибок

clear

a=1;b=0.5;c=0.03;x1=0;x2=1;n=300;err=0.1;

k=eye(n); %преобразующая матрица

%(единичная для сглаживания)

[f,f1,x,dx]=test(a,b,c,n,x1,x2,err); %формирование тестовой функции,

%f-точная функция,

%f1-экспериментальная,dx-шаг,

%x-ось абсцисс(для графика)

[dif,omega,w,v,u]=matrixs(n,err,dx);%матрицы:dif-дифференцирования

%(второго порядка)

% omega-стабилизатор,

% w-информационная матрица,

% v-ковариационная матрица ошибок,

% u-матрица, необходимая при учете неравенств

alf=alfa(f1,v,k,omega); % параметр регуляризации (одношаговая оценка)

s=(1/sqrt(alf))*k*inv(dif); % множитель для формирования

% вспомогательной системы

ss=[s u];

x0=zeros(1,2*n);

epse=0.000001;epsne=0.000001;

c=eye(2*n);

d=zeros(1,2*n);

ff=inv(k'*w*k+alf*omega)*k'*w*f1';

ft=algorithm4(ss,f1,c,d,x0,epse,epsne);

for i=1:n

ftt(i)=ft(i);

end

ftt=s*ftt';

ftt=ftt/max(ftt);

plot(x,f,x,f1,x,ftt,x,ff)

% Метод статистической регуляризации + метод опорных векторов

% с составным шагом

% a,b,c- параметры лоренциана: a- амплитуда, c- полуширина,

% в- положение центра

% x1,x2-границы интервала измерений, n- число измерений,

% err- уровень ошибок

clear

a=1;b=0.5;c=0.03;x1=0;x2=1;n=100;err=0.2;

k=eye(n); % преобразующая матрица

% (единичная для сглаживания)

[f,f1,x,dx]=test(a,b,c,n,x1,x2,err); % формирование тестовой функции

% f-точная функция,

% f1-экспериментальная,dx-шаг

% x-ось абсцисс(для графика)

[dif,omega,w,h,v]=matrixs(n,err,dx); % матрицы: dif-дифференцирования

%(2 порядка)

% omega-стабилизатор,

%w-информационная матрица,

% v-ковариационная матрица ошибок

alf=alfa(f,v,k,omega); % параметр регуляризации

% (одношаговая оценка)

s=(1/sqrt(alf))*inv(dif); % множитель для формирования

% вспомогательной системы

s1=sqrt(alf)*dif; % множитель для перехода от

% решений системы к

% искомым данным

systmatrix=[s h]; % матрица системы

for i=1:2*n % начальное приближение

x0(i)=0;

end

epse=0.00001;epsne=0.00001;

c=eye(2*n) ;

ft=algorithm3(a,b,c,d,x0,epse,epsne);

ft=s*ft';

plot(x,f,x,f1,x,ft)

Для исследования влияния учета условий (3.14) на качество восстановления изображения были проведены математические эксперименты, которые продемонстрировали значительное повышение качества восстановления изображений при учете априорной информации, представимой в виде неравенств. Так для случая устранения случайного шума, составляющего 10% от максимального уровня сигнала среднеквадратичное отклонение восстановленного сигнала от модельной функции изменилось с 0.4 (без учета неотрицательности) до 0.31 (с учетом неотрицательности). Результаты математических экспериментов приведены на Рис.3 и Рис.4.

Алгоритм может быть использован для широкого класса задач обработки изображений (увеличения качества фотографических изображений, восстановлении изображений в компьютерной томографии и т.п.). Он может быть использован и для обработки многомерных изображений.

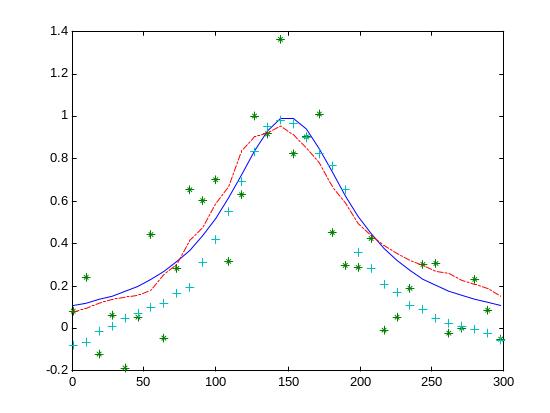
Рис.3. Результаты сглаживания “экспериментальных данных” с учетом неотрицательности. Сплошная кривая – модельная функция, * – “ экспериментальные данные”, + – сглаживание без учета неотрицательности, щтрих-пунктирная линия – с учетом неотрицательности.

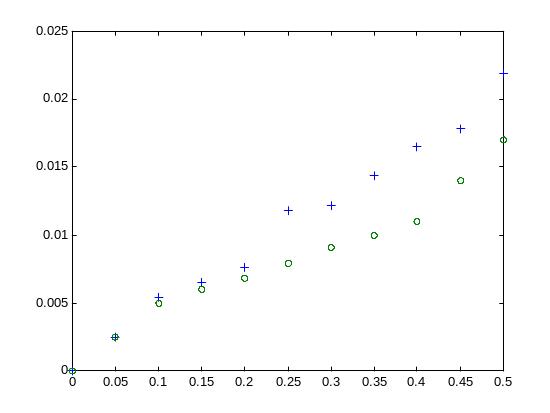
Рис.4. Среднеквадратичная мера отличия восстановленного сигнала от модельного в зависимости от уровня шума. + – без учета неотрицательности, о – с учетом неотрицательности.