15. Метод минимальных поправок, метод минимальных невязок

Рассматривается СЛУ и итерационный процесс:

(1)

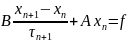(2)

- невязка, (3)

- поправка

Метод минимальных поправок заключается в том, чтобы выбрать из условия: минимально.

Подействуем на (3) матрицей , вычтем , затем подействуем матрицей :

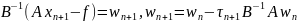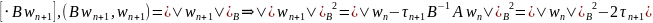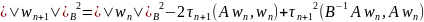., , . Минимум достигается при 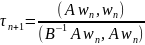. (4)

Метод минимальных невязок. Метод минимальных невязок состоит в выборе для минимизации невязки. Рассмотрим метод при . Тогда . Получаем 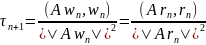(5)

и метод минимальных поправок принимает вид 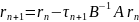(6)

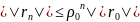Теорема. Пусть А — симметричная положительно опреде­ленная матрица. Для погрешности метода минимальных невязок выполняется оценка , или , где

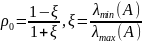
Д-во. 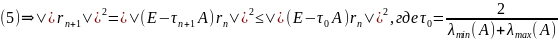(т.к. при , выбранном по (5), 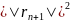минимально при любом другом значение справа увеличится)

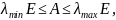т.к.

аналогично

Теорема д-на.

Теорема. Пусть A и B - симметричные положит-е матрицы. Тогда для погрешности метода мин. поправок верна оценка: , где

Д-во. Сначала докажем лемму.

Лемма. Собственные значения матриц совпадают с собственными значениями обобщенной спектральной задачи

Д-во леммы.

Пусть - соб-е значение м-цы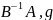 - соответствующий соб-й вектор. 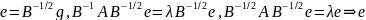- соб-й вектор, соотв-й соб-му знач-ю матрицы

Лемма д-на

Продолжим д-во теоремы.

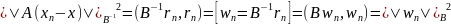
Обозначим 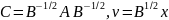, тогда (7)

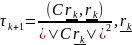Метод мин. невязок для (7) примет вид где - невязка, т.е. 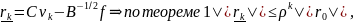(8)

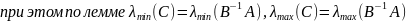
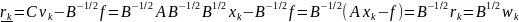
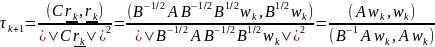- совпадает с 4

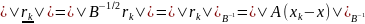. Тогда из (8) следует утверждение теоремы.

Теорема д-на

16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.

Ищем приближение к решению системы вида

(1)

Метод скорейшего спуска.

Рассмотрим явный метод

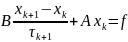(2)

и выберем итерационный параметр из условия минимума при заданном векторе , где

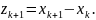
Имеем:

,

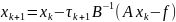Поскольку погрешность удовлетворяет уравнению

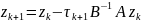
имеем

где невязка,

поправка,

где 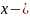точное решение,

Следовательно, 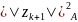будет минимальной если метод явный (то есть, 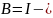единичная матрица) и

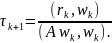
Теорема.

Пусть A - симметрическая положительно определённая матрица. Для метода скорейшего спуска выполняется оценка:

где

Преимущество метода: не нужно знать границ ( ).

Метод сопряжённых градиентов.

Этот метод является двухшаговым итерационным методом, то есть для нахождения новой итерации используются две предыдущие итерации . Следовательно, здесь возрастает требуемый объём памяти, нужно помнить не только вектор , но и 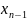. Применение двухшаговых методов оправдывается тем, что при правильном выборе итерационных параметров скорость сходимости будет выше, чем у одношаговых методов. Например, рассматриваемый метод сопряжённых градиентов сходится при любом начальном приближении за конечное число итераций.

Пусть 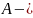матрица системы и 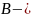симметричная положительно определённая матрица. Рассмотрим следующий класс неявных двухшаговых итерационных методов:

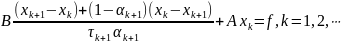.0 (1)

Первый шаг находится по одношаговой формуле, которая получается при :

.

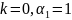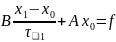где 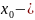произвольное начальное приближение.

Задача состоит в выборе таких коэффициентов что при любом 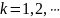была минимальной оценка . Тогда получим:

,

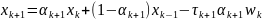где .

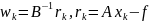Коэффициенты считаются по следующим формулам:

.

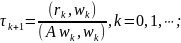
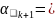Тогда будет верна

Теорема.

Пусть 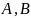- симметрические положительно определённые матрицы. Тогда для погрешности метода сопряжённых градиентов выполнена оценка:

,

где 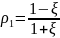, где , где .
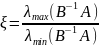