
- •1. Вычислительный эксперимент. Типы погрешностей. Погрешность округления. Представление чисел на эвм.
- •2. Накопление погрешностей округления.
- •3. Метод Гаусса. Подсчет числа действий. Метод Гаусса с выбором главного элемента.
- •4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.
- •5.Обусловленность, устойчивость решения слу
- •6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
- •7.Достаточное условие сходимости стационарных итерационных методов.
- •8. Сходимость метода Якоби, Зейделя, метода простых итераций.
- •9. Необходимое и достаточное условие сходимости.
- •10. Оценка скорости сходимости итерационных методов в случае симметричных матриц a и b
- •11. Многочлен Чебышева с нормировкой по старшему коэффициенту.
- •12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
- •13. Явный итерационный метод Чебышева
- •14. Неявный итерационный метод Чебышева.
- •15. Метод минимальных поправок, метод минимальных невязок
- •16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.
- •17. Интерполирование и приближение функций. Интерполяционная формула Лагранжа.
- •18. Погрешность интерполяции. Оптимальный выбор узлов интерполяции.
- •19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.
- •20. Интерполяция кубическими сплайнами.
- •21. Скорость процесса интерполяции кубическими сплайнами.
- •22. Наилучшее приближение в гильбертовом пространстве.
- •23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
- •24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
- •25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.
- •26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.
- •27. Сходимость метода простых итераций
- •28. Метод Ньютона. Сходимость метода Ньютона.
- •29. Метод Ньютона в случае кратных корней. Односторонние приближения по методу Ньютона.
- •30. Итерационные методы решения снлу. Сходимость метода простых итераций
- •31. Производная от оператора. Метод Ньютона для систем нелинейных уравнений.
- •32. Метод Рунге-Кутта второго порядка. Семейство методов второго порядка. Методы третьего и четвертого порядка.
- •1. Методы второго порядка
- •2. Методы третьего порядка.
- •3. Методы четвертого порядка.
- •33. Доказательство сходимости метода Рунге-Кутта.
- •34. Многошаговые разностные методы. Погрешность аппроксимации метода.
- •35. Устойчивость многошагового метода по начальным данным.
- •36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
- •37. Разностная аппроксимация Пуассона. Порядок аппроксимации
- •38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
- •39.Разностный оператор Лапласа. Собственные значения и собственные функции
- •40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
- •1) Метод простых итераций.
- •2) Метод Чебышева.
- •3) Метод сопряжённых градиентов.
- •45. Асимптотическая устойчивость разностных схем.
- •46. Вариационные методы в математической физике.
- •47. Метод Ритца.
- •48. Метод Галеркина.
12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
Найти
степени n, наименее отклоняющийся от
нуля на [a; b] среди всех мнгч-в степени
n, принимающих значение 1 при x=0. Таким
мнгл-м является мнгч
 .
При b>a>0 получим, что:
.
При b>a>0 получим, что:
 где
где

Обозначим:
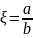 ,
,
 =>
=>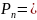
Далее пользуемся тождествами:
 ,
при
,
при
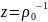 =>
=>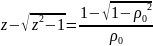 .
Подставим выражение для
.
Подставим выражение для
 и
получим:
и
получим:
 ,
,
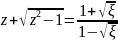 .
.
Получим:
,
где

Т. о.
 ,
где
,
где
 нули такие же, как у мнгч Чебышева:
нули такие же, как у мнгч Чебышева:
 ,
k=1, …, n
,
k=1, …, n
Рассмотрим пример.
Для мнгч
 подобрать
подобрать
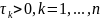 так,
чтобы минимизировать величину
так,
чтобы минимизировать величину
 ,
,
 .
Ясно, что
.
Ясно, что
 => мнгч нормирован значением в нуле.
Задача будет решена, если подберем
=> мнгч нормирован значением в нуле.
Задача будет решена, если подберем
 так,
чтобы
так,
чтобы
 .
.
Заметим, что
корнями функции
 являются значения
являются значения
 .
Для решения задачи эти корни должны
совпадать с корнями мнгч Чебышева. Если
обозначим
.
Для решения задачи эти корни должны
совпадать с корнями мнгч Чебышева. Если
обозначим
 -
корни
-
корни
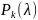 ,
то должно выполняться
,
то должно выполняться
 => Находим
из
уравнения
=> Находим
из
уравнения
 => при таком выборе
=> при таком выборе
 ,
где
,
где
 ,
,
,
,
 .
.
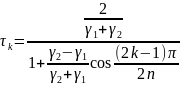 ,
k=1, …, n.
,
k=1, …, n.
Т.о. доказана
лемма:
 )
достигается при
)
достигается при
 определенных
по формуле и равен
,
k=1, …, n и равен
определенных
по формуле и равен
,
k=1, …, n и равен
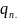
13. Явный итерационный метод Чебышева
Рассмотрим (1)
и рассматриваем
итерационный процесс 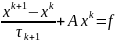 (2)
(2)
И считаем, что
задана норма
 .
.
Теорема.
Пусть A - симметричная, положительно
определенная матрица.
 ее наименьшие и наибольшие собственные
значения. Пусть задано число итераций
n. Среди методов вида (2) наименьшую
погрешность имеет метод, для которого
ее наименьшие и наибольшие собственные
значения. Пусть задано число итераций
n. Среди методов вида (2) наименьшую
погрешность имеет метод, для которого
 (3).
(3).
 ,
,
 ,
k=1, …, n (4).
,
k=1, …, n (4).
Если
определено по формулам (3) и (4), то
 ,
,
где
(6).
,
 .
.
Д-во: Пусть
 ,
тогда
,
тогда
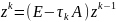 =>
=> .
.
 где
где
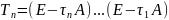 .
.
Пусть
 собственные
значения матрицы А, тогда у
собственные
значения матрицы А, тогда у
 собственные
значения будут:
собственные
значения будут:
 .
Т.к.
.
Т.к.
 - симметрическая, то
- симметрическая, то
 - спектральный радиус.
- спектральный радиус.
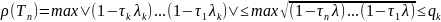 (первый максимум по
,
второй максимум по
(первый максимум по
,
второй максимум по
 )
=> неравенство (5) доказано.
)
=> неравенство (5) доказано.
Осталось доказать, что лучше, чем эти, параметров нет.
Пусть
 - другой набор параметров =>
- другой набор параметров => ,
при
,
при
 мнгч нормирован.
мнгч нормирован.
 =>
=>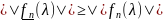 и пусть
и пусть
 то число, при котором
то число, при котором
 (достигается
максимум). Тогда найдется матрица и
элемент
(достигается
максимум). Тогда найдется матрица и
элемент
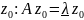 .
Тогда
.
Тогда
 .
И т.к.
-
собственный вектор, то
.
И т.к.
-
собственный вектор, то
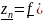 =>
=>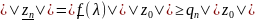 .
ЧТД
.
ЧТД
Теорема.
Пусть А - симметрическая, положительно
определенная матрица. Если точные
границы спектра
 и
и
 неизвестны,
но известны их границы
неизвестны,
но известны их границы
 ,
и параметры
определены
согласно формулам (3) и (4), где
,
и параметры
определены
согласно формулам (3) и (4), где
 ,
то для погрешности справедлива оценка
(5), где
,
то для погрешности справедлива оценка
(5), где
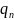 определяется по формуле (6), в которой
.
определяется по формуле (6), в которой
.
Д-во:
 , нужно оценить
, нужно оценить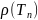 - спектральный радиус оператора
.
- спектральный радиус оператора
. (первый максимум по
(первый максимум по второй
максимум по
второй
максимум по
 ).
ЧТД
).
ЧТД
14. Неявный итерационный метод Чебышева.
 + A
= f,
k
= 0,1,…
задан,
(14)
+ A
= f,
k
= 0,1,…
задан,
(14)
с
симметричной положительно определённой
матрицей B
и переменными параметрами
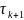 .
Скорость сходимости метода (14) будет
определяться отношением
.
Скорость сходимости метода (14) будет
определяться отношением
 минимального и максимального собственных
чисел обобщённой задачи:
минимального и максимального собственных
чисел обобщённой задачи:
Aμ = λBμ (15)
При
соответствующем выборе матрицы B
это отношение будет больше чем
 ,
а следовательно итерационный метод
(14) будет сходиться быстрее, чем явный
метод.
,
а следовательно итерационный метод
(14) будет сходиться быстрее, чем явный
метод.
Теория неявных итерационных методов легко сводится к теории явного метода. В ходе доказательства будет использоваться теорема: Теорема 1 из предыдущего вопроса(вставить сюда её формулировку)
Для неявного чебышевского метода справедлива теорема:
Теорема.
Пусть
A
и B-
симметричные положительно определённые
матрицы, а
 - соответственно наименьшее и наибольшее
собственные значения задачи (15). Пусть
задано число итераций n.
Метод (14) имеет минимальную погрешность
- соответственно наименьшее и наибольшее
собственные значения задачи (15). Пусть
задано число итераций n.
Метод (14) имеет минимальную погрешность
 ,
если параметры
определить так:
,
если параметры
определить так:
 k = 1,2,…,n
(3)
k = 1,2,…,n
(3)
 ,
k = 1,2,…,n (4)
,
k = 1,2,…,n (4)
при этом справедлива оценка
 ,
(16)
,
(16)
где
 (17)
(17)
Доказательство.
Погрешность
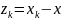 удовлетворяет однородному уравнению
удовлетворяет однородному уравнению
 + A
+ A = 0, k = 0,1,…
= 0, k = 0,1,…
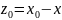 (18)
(18)
Умножим
уравнение (18) на матрицу
 и обозначим
и обозначим
 =
=
 . Тогда получим уравнение
. Тогда получим уравнение
 + C
= 0, k
= 0,1,…
+ C
= 0, k
= 0,1,…
 (19)
(19)
где C = A . Нужно проверить выполнение условий теоремы 1 по отношению к матрице C.
Матрица
C
является симметричной и положительно
определённой, причём её спектр совпадает
со спектром обобщённой задачи на
собственные значения (15). В частности
 является минимальным собственным числом
является минимальным собственным числом
 матрицы C,
а
матрицы C,
а
 - максимальным. Следуя теореме 1, выберем
параметры
согласно (3), (4), где ξ =
- максимальным. Следуя теореме 1, выберем
параметры
согласно (3), (4), где ξ =
 .
Тогда для решения уравнения (19) будет
выполняться оценка
.
Тогда для решения уравнения (19) будет
выполняться оценка
 ≤
≤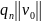
Подставляя сюда = , k=0,…,n получим
 ≤
≤
т.е. придём к требуемой оценке (16). Теорема доказана.
