9. Необходимое и достаточное условие сходимости.

Пусть дана система уравнений:

Ax = f, (1)

где A =[ ], i,j = 1,2,…m, - вещественная квадратная матрица, имеющая обратную, и x=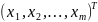 , f= . Канонической формой одношагового итерационного метода называется его запись в виде:

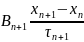+ A = f , n = 0,1,… (2)

где n – номер итерации, - заданное начальное приближение, =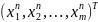 . Матрица и числа 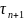> 0 задают тот или иной конкретный итерационный метод.

Мы рассмотрим стационарный итерационный метод

+ A = f (3)

В таких методах матрица B и числовой параметр τ не зависят от номера итерации n.

Погрешность итерационного метода (3) = , где x – точное решение системы (1), удовлетворяет уравнению

+ A = 0, n = 0,1,…, = (4)

которое отличается от уравнения (3) лишь тем, что является однородным.

Сходимость итерационного метода (3) означает, что → 0 в некоторой норме при n→беск. Переписывая уравнение (4) в разрешённой относительно 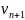форме

= S (5)

где

S = E – τ A (6)

видим, что свойство сходимости итерационного метода целиком определяется матрицей S. Необходимые и достаточные условия сходимости в терминах S приведены далее. Матрица S называется матрицей перехода от n-й итерации к (n+1)-й.

При исследовании сходимости будем рассматривать векторы и x как элементы m-мерного линейного пространства H, в котором введена норма вектора x. нормой матрицы A, подчинённой данной норме вектора, называется число

=

Норму вектора в пространстве H можно ввести различным образом. Нам, прежде всего, потребуется норма

Подчинённая ей норма матрицы A выражается через элементы матрицы A следующим образом:

Теорема. Итерационный метод (3) сходится при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы S = E – τ A по модулю меньше единицы.

Доказательство. Представим уравнение (4) для погрешности = в виде (5)-(6). Докажем сначала необходимость условий теоремы.

Предположим, что матрица S имеет собственное число s, для которого > 1, и покажем, что в этом случае можно так подобрать начальное приближение , чтобы погрешность = неограниченно возрастала при n→беск. Пусть μ – собственный вектор матрицы S, отвечающий собственному числу s, > 1. Возьмём в качестве начального приближения вектор , так что начальная погрешность =μ. тогда из уравнения (5) получим:

и 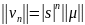→беск. при n→беск. Если не→0 при n→беск.

Доказательство достаточности условий теоремы приведём сначала в предположении, что матрица S имеет m линейно независимых собственных векторов. Пусть , k=1,2,…,m – собственные числа матрицы S и , k=1,2,…,m – отвечающие им линейно независимые собственные векторы. Разложим начальную погрешность = по векторам :

Тогда получим

В любой норме справедлива оценка

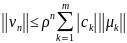(11)

где ρ = – спектральный радиус матрицы S. Из оценки (11) в силу предположения теоремы о том, что ρ<1, и следует сходимость метода.

В общем случае, когда система собственных векторов матрицы S не является полной, доказательства достаточности условий теоремы проводится с помощью приведения S к жордановой форме. Для любой квадратной матрицы S порядка m существует невырожденная матрица P такая, что матрица имеет жорданову каноническую форму

где 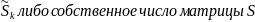, либо жорданова клетка вида

а - собственные числа матрицы S.

Помимо обычной жордановой формы нам потребуется ещё так называемая модифицированная жорданова форма матрицы S. Она строится следующим образом.

Применим к матрице преобразование подобия 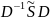с диагональной матрицей D = diag[1, ε, … , ], где ε – любое положительное число. Нетрудно убедиться, что матрица

(примечание человека, набирающего формулу: )

имеет ту же блочно-диагональную структуру, что и матрица , однако жордановы клетки имеют теперь следующий вид:

Матрицы S и связаны равенством:

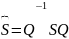, Q=PD (12)

Матрица имеет в каждой строке не более двух отличных от нуля элементов, поэтому

(13)

где - спектральный радиус матрицы S, т.е. ρ(S) = .

Ранее (не в этом вопросе) было доказано, что подчинённая норма матрицы удовлетворяет неравенству:

ρ(S) (14)

Покажем теперь, что можно найти такую норму вектора, для которой подчинённая норма матрицы станет сколь угодно близкой к её спектральному радиусу. Точнее, справедливо следующее утверждение:

Лемма 1. Для любого ε>0 существует норма вектора такая, что для подчинённой нормы матрицы справедливо неравенство

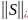≤ ρ(S) + ε (15)

Доказательство. Воспользуемся преобразованием (12) и определим норму вектора равенством

для любого вектора y . Для подчинённой нормы матрицы S имеем

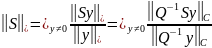
Обозначая 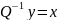и учитывая (12), (13), получим отсюда

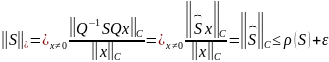
что и требовалось. Завершим доказательство теоремы.

Из уравнения (5) получим

= n=0,1,… (16)

Пусть - норма, для которой выполнено неравенство (15). По условию теоремы , поэтому существует такое, что ≤ . Из (16) получим оценку

≤ (17)

из которой следует, что → 0 при любых начальных приближениях.