
- •1. Вычислительный эксперимент. Типы погрешностей. Погрешность округления. Представление чисел на эвм.
- •2. Накопление погрешностей округления.
- •3. Метод Гаусса. Подсчет числа действий. Метод Гаусса с выбором главного элемента.
- •4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.
- •5.Обусловленность, устойчивость решения слу
- •6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
- •7.Достаточное условие сходимости стационарных итерационных методов.
- •8. Сходимость метода Якоби, Зейделя, метода простых итераций.
- •9. Необходимое и достаточное условие сходимости.
- •10. Оценка скорости сходимости итерационных методов в случае симметричных матриц a и b
- •11. Многочлен Чебышева с нормировкой по старшему коэффициенту.
- •12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
- •13. Явный итерационный метод Чебышева
- •14. Неявный итерационный метод Чебышева.
- •15. Метод минимальных поправок, метод минимальных невязок
- •16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.
- •17. Интерполирование и приближение функций. Интерполяционная формула Лагранжа.
- •18. Погрешность интерполяции. Оптимальный выбор узлов интерполяции.
- •19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.
- •20. Интерполяция кубическими сплайнами.
- •21. Скорость процесса интерполяции кубическими сплайнами.
- •22. Наилучшее приближение в гильбертовом пространстве.
- •23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
- •24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
- •25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.
- •26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.
- •27. Сходимость метода простых итераций
- •28. Метод Ньютона. Сходимость метода Ньютона.
- •29. Метод Ньютона в случае кратных корней. Односторонние приближения по методу Ньютона.
- •30. Итерационные методы решения снлу. Сходимость метода простых итераций
- •31. Производная от оператора. Метод Ньютона для систем нелинейных уравнений.
- •32. Метод Рунге-Кутта второго порядка. Семейство методов второго порядка. Методы третьего и четвертого порядка.
- •1. Методы второго порядка
- •2. Методы третьего порядка.
- •3. Методы четвертого порядка.
- •33. Доказательство сходимости метода Рунге-Кутта.
- •34. Многошаговые разностные методы. Погрешность аппроксимации метода.
- •35. Устойчивость многошагового метода по начальным данным.
- •36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
- •37. Разностная аппроксимация Пуассона. Порядок аппроксимации
- •38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
- •39.Разностный оператор Лапласа. Собственные значения и собственные функции
- •40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
- •1) Метод простых итераций.
- •2) Метод Чебышева.
- •3) Метод сопряжённых градиентов.
- •45. Асимптотическая устойчивость разностных схем.
- •46. Вариационные методы в математической физике.
- •47. Метод Ритца.
- •48. Метод Галеркина.
6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
Рассмотрим обычную систему линейных уравнений:
(1)

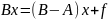 (2)
(2)
Если (B-A) - сравнительно малая величина можно решать:
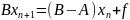 - Итерационный метод без параметра.
- Итерационный метод без параметра.
Рассмотрим:

(2)

Иногда удобно
на каждом шагу менять
 и
и
 :
:

 (3)
(3)
(3) - каноническая форма одношагового итерационного метода
Если
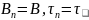 -
то метод называю стационарным.
-
то метод называю стационарным.

Если
 то метод называют явным.
то метод называют явным.

Если
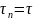 -
то метод называется - метод простых
итераций, а если
-
то метод называется - метод простых
итераций, а если
 -
то метод называется - метод Ричардсона.
-
то метод называется - метод Ричардсона.
Обозначим:
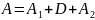 ,
,
где
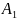 -
нижнетреугольная(
-
нижнетреугольная( ),
),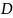 -
диагональнаяl(
-
диагональнаяl( ),
),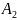 -
верхнетреугольная(
-
верхнетреугольная( )
)
1) Метод Якоби
Частный случай
стационарного процесса


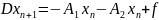
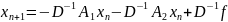
В координатном виде:
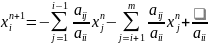 ,
m - размерность A
,
m - размерность A
2) Метод Зейделя
Частный случай
стационарного процесса

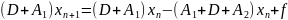
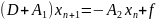

В координатах
 ,
,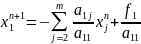 ,
,
7.Достаточное условие сходимости стационарных итерационных методов.
(1)
(2)
Говорят что
итерационный метод (2) сходится, если
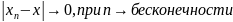 .
.
Будем считать
что решение задачи (1) ищется в линейном
вещественном пространстве
 ,
со скалярным произведением
,
со скалярным произведением
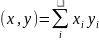 ,
матрица A вещественная.
,
матрица A вещественная.
Опр.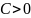 (положительно
- определенная), если
(положительно
- определенная), если
 ,
,

Лемма.
Если
,
то

Док-во:
Пусть матрица
-симметричная,
тогда существует ортогональная система
собственных векторов { },
такая что
},
такая что
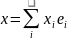 ,
где
,
где
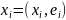 ,а
,а
 и
и
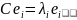 ,
тогда
,
тогда
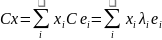 ,
,
тогда, ,
замечаем, что для любого
,
замечаем, что для любого
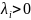 ,
т.е.
,
т.е.

тогда
 ,
где
,
где
 .
.
В общем случае,
 матрица
матрица
 симметрична и для нее справедливо
симметрична и для нее справедливо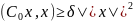 .
Т.е.
.
Т.е. .
.
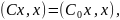 если
если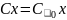
Примечание:
 -
транспонированная.
-
транспонированная.
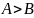 значит
значит

Теорема.
Пусть
 -
симметричная, положительно-определенная
матрица,
-
симметричная, положительно-определенная
матрица,
 и выполнена формула
и выполнена формула
 ,
тогда итерационный процесс (2) сходится.
,
тогда итерационный процесс (2) сходится.
Док-во:
Пусть
 ,
тогда
,
тогда
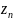 удовлетворяет
удовлетворяет
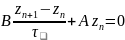 .
.
Докажем, что
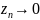 ,
введем величину
,
введем величину
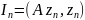
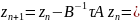 ,
,
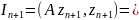
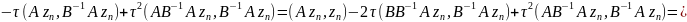
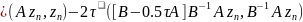 ,
,
 последовательность
последовательность
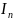 не возрастает и ограничена снизу
не возрастает и ограничена снизу
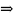 сходится
сходится
 отсюда
отсюда
 .
.
Обозначим
 ,
т.к.
,
т.к.

Теорема доказана.
8. Сходимость метода Якоби, Зейделя, метода простых итераций.
Следствие
1. Пусть А - симметричная,
положительно-определенная матрица с
диагональным преобладанием, т.е.
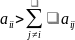 ,
тогда метод Якоби сходится.
,
тогда метод Якоби сходится.
Док-во. Необходимо
доказать, что
,
где
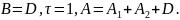
т.е. надо доказать, что
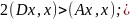

Следствие
2. Пусть А - симметричная,
положительно-определенная матрица и
 ,
тогда метод верхней релаксации сходится
при
,
тогда метод верхней релаксации сходится
при
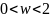 .
В частном случае метод Зейделя (
.
В частном случае метод Зейделя (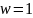 ).
).
Док-во.
Необходимо доказать, что
,
где
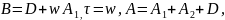
 т.к.
т.к.

1)
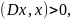 т.к.
т.к.
2)
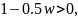 т.е.
т.е.

Доказано.
Рассмотрим
вопрос о сходимости метода простых
итераций
 (1) с симметричной положительно-определенной
матрицей
.
Метод сходится при условии
(1) с симметричной положительно-определенной
матрицей
.
Метод сходится при условии
 (2).
(2).
Какие ограничения
на параметр
накладывает условие(2)? Пусть
 ,— собственные значения матрицы
,
расположенные в порядке возрастания.
Условие (2) эквивалентно тому, что все
собственные значения матрицы
,— собственные значения матрицы
,
расположенные в порядке возрастания.
Условие (2) эквивалентно тому, что все
собственные значения матрицы
 положительны. Достаточно потребовать
положительности минимального собственного
числа этой матрицы, равного
положительны. Достаточно потребовать
положительности минимального собственного
числа этой матрицы, равного
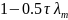 .
Таким образом, итерационный метод (1)
сходится, если
.
Таким образом, итерационный метод (1)
сходится, если
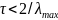 (3),
где
(3),
где
 -максимальное
собственное число матрицы
.
-максимальное
собственное число матрицы
.
Условие (3)
необходим для сходимости (1), т.е. если
нарушено (3), то найдется начальное
приближение
 ,
при котором
,
при котором
 не стремится к нулю при
не стремится к нулю при
 .
.
Докажем
последнее утверждение. Возьмем в качестве
начального приближения вектор
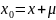 ,
где
,
где
 — точное решение задачи
,
а
— точное решение задачи
,
а
 ,
— собственный вектор матрицы
,
отвечающий собственному числу
,
— собственный вектор матрицы
,
отвечающий собственному числу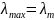 ,
т. е.
,
т. е.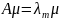 .
При таком выборе начального приближения
имеем
.
При таком выборе начального приближения
имеем
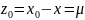 .
Т.к.
.
Т.к.
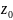 удовлетворяет однородному уравнению
и
удовлетворяет однородному уравнению
и
 получим
получим
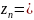
и, следовательно, .
Если
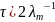 ,
то
,
то
 не
стремится к нулю при
.
Если же
,
то
не
стремится к нулю при
.
Если же
,
то и
и
 при
.
Таким образом, условие (3) необходимо и
достаточно для сходимости метода простых
итераций (1).
при
.
Таким образом, условие (3) необходимо и
достаточно для сходимости метода простых
итераций (1).
