4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.

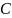(1) сводится к виду , где – верхнетреугольная матрица. Обозначим . Тогда

, где

Таким образом, если метод Гаусса применим, то может быть представлена в виде произведения нижнетреугольной матрицы (с ненулевыми элементами на главной диагонали) на верхнетреугольную (с единичной главной диагональю). Итак метод Гаусса имеет этапы: 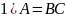(прямой ход) 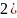решается система решается систем

Теорема об разложении. Пусть все угловые миноры матрицы отличны от нуля. Тогда может быть представлена единственным образом в виде произведения 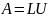, где – верхнетреугольная матрица с единичной диагональю.

Доказательство (по индукции)

1) Докажем для матрицы 2-го порядка нужно найти

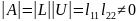
2) Пусть доказано для матрицы 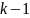порядка

3) доказать для матрицы порядка и обозначим

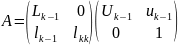
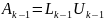
Из предположения индукции следует существование , ,

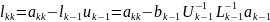
Таким образом разложение порядка существует.

Докажем единственность

и и

Следствие Метод Гаусса можно применять 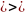когда все угловые миноры .

Теорема

Метод Гаусса с выбором главного элемента по строке (столбцу) применим

5.Обусловленность, устойчивость решения слу

Говорят, что задача поставлена корректно, если ее решение существует и единственно и если оно непрерывно зависит от входных данных. Последнее свойство назы­вается также устойчивостью относительно входных данных.

Рассматривается m-мерное пространство H с нормами. Норма - численная функция, удовлетворяющая аксиомам:

1)

2)

3)

Для матрицы норму определяем по формуле:

Очевидно , или (1)

Рассмотрим СЛУ с точным решением

и СЛУ с приближенным :

Обозначим изменение правой части за , а изменение полученного решения , .

Определение. Система называется устойчивой по правой части, если

Пусть матрица A является невырожденной, .Тогда . (2)

Тогда очевидно, что СЛУ является устойчивой по правой части. Оценим погрешность

Определение. 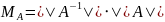- число обусловленности матрицы A.

Свойства :

1)

2) 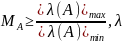- собственные числа матрицы A.

3)

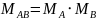
Определение. 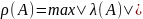- спектральный радиус.

Докажем свойство 2. Для этого сначала докажем, что . Действительно, пусть e - вектор, соответствующий максимальному по модулю собственному значению: 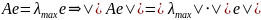. С другой стороны, (3)

Если - собственное значение A, то - собственное значение . (Действительно, ). Следовательно, (4)

Из (3) и (4) . Свойство 2 доказано.

Замечание. Пусть в пространстве H норма определяется через скалярное произведение и матрица A - симметрическая. Тогда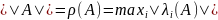 . Действительно, если А - симм-я, то у нее есть полная система ортонормированных собственных векторов (известно из лин. алгебры) Тогда , . Но в то же время ранее уже доказано, что , следовательно

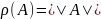
Теперь рассмотрим случай, когда матрица A также задана приближенно. .

Теорема. Пусть A имеет обратную и выполнено условие Тогда матрица имеет обратную и справедлива следующая оценка относительной погрешности:

Д-во. Сначала докажем лемму.

Лемма. Пусть С - невырожденная квадратная матрица, . Тогда

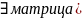
Д-во леммы.

Следовательно , значит матрица (E+C) обратима. Обозначим

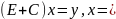
Лемма д-на. Продолжим д-во теоремы

Тогда вып-на лемма: .

Обозначим

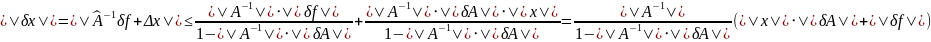
Т.к. 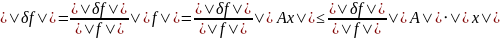, то

Теорема д-на.